Applications of Thermodynamics Work – Overview, Expansion

Applications of Thermodynamics: In everyday conversation, when individuals talk about work, they usually mean putting effort into something. We might “work on a school project” or “lift books from the ground to a shelf. Work, on the other hand, has a very particular meaning in thermodynamics: it is the energy required to move an object against a force.

Work is one of the most basic ways that energy enters or exits a system, and it is measured in Joules. Many chemical reactions generate gases that are capable of doing mechanical work or producing heat. It’s essential that we quantify these changes and link them to internal energy shifts. Let us see how!

What is Work?

Work is a form of energy. It is defined as the energy transferred by a system to its surroundings in thermodynamics. Only mechanical work, i.e. pressure-volume work, will be discussed in this section.

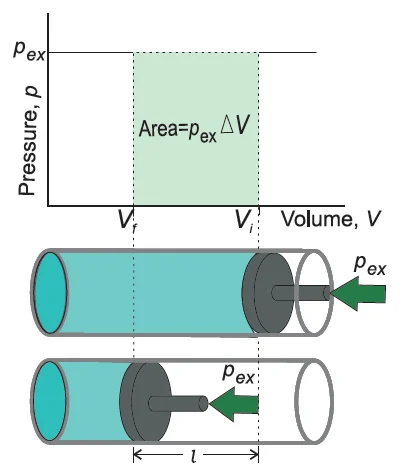
Consider a cylinder containing one mole of an ideal gas. A frictionless piston is fitted in the cylinder. Let the total volume of the gas be \({{\rm{V}}_{\rm{i}}}\) and pressure of the gas inside is \({\rm{p}}{\rm{.}}\) 

If the external pressure \(\left( {{{\rm{p}}_{{\rm{ex}}}}} \right)\) is larger than the internal pressure \(\left( {\rm{p}} \right){\rm{,}}\) the piston will travel inward until the internal pressure equals \({{{\rm{p}}_{{\rm{ex}}}}}.\) Let us assume that this change is achieved in a single step, and the final volume becomes \({{\rm{V}}_{\rm{f}}}.\) During the compression, the piston moves a distance \(\left( {\rm{l}} \right){\rm{,}}\) and the area of cross-section of the piston is \({\rm{A}}.\)

Volume change \({\rm{ = l \times A = \Delta V = }}{{\rm{V}}_{\rm{f}}}{\rm{ – }}{{\rm{V}}_{\rm{i}}}\)

We know that pressure\({\rm{ = force \div area}}\)

Or, Force\({\rm{ = Pressure \times Area}}\)

So, force on piston\({\rm{ = }}{{\rm{p}}_{{\rm{ex}}}}{\rm{ \times A}}\)

If \({\rm{w}}\) is the work done on the system by the movement of the piston, then-

\({\rm{w = force \times distance}}\)

\({\rm{ = }}{{\rm{p}}_{{\rm{ex}}}}{\rm{ \times A \times l}}\)

\({\rm{ = }}{{\rm{p}}_{{\rm{ex}}}}{\rm{( – \Delta V)}}\)

\({\rm{ = \, – }}{{\rm{p}}_{{\rm{ex}}}}{\rm{\Delta V}}\)

\({\rm{ = \, – }}{{\rm{p}}_{{\rm{ex}}}}\left( {{{\rm{V}}_{\rm{f}}}{\rm{ – }}{{\rm{V}}_{\rm{i}}}} \right){\rm{ \ldots \ldots \ldots (2)}}\)

The negative sign indicates that if the system is compressed \(\left( {{{\rm{V}}_{\rm{f}}}{\rm{ – }}{{\rm{V}}_{\rm{i}}}} \right)\) will be negative, and negative multiplied by negative will be positive. As a result, the work sign obtained is positive. If the pressure changes in a number of finite steps rather than being constant at each stage of compression, the work done on the gas will be summed over all of the steps and equal to – 

\(\sum {\rm{\Delta }} {\rm{pV}}\)

Suppose the pressure is not constant but changes in such a way that it is always infinitesimally greater than the pressure of the gas. In that case, the volume reduces by an infinitesimal amount, \({\rm{dV,}}\) at each stage of compression. In this situation, the relation is used to calculate the work done on the gas is given by-

\({\rm{w = \, – }}\int_{{{\rm{V}}_{\rm{i}}}}^{{{\rm{V}}_{\rm{f}}}} {{{\rm{p}}_{{\rm{ex}}}}} {\rm{dV}}\)

Here, \({{\rm{p}}_{{\rm{ex}}}}\) at each stage is equal to \(\left( {{{\rm{p}}_{{\rm{in}}}}{\rm{ + dp}}} \right)\) in case of compression. 

Under similar conditions, in an expansion process, the external pressure is always less than the pressure of the system i.e., \({{\rm{p}}_{{\rm{ex}}}}{\rm{ = }}\left( {{{\rm{p}}_{{\rm{in}}}}{\rm{ – dp}}} \right){\rm{.}}\) 

Considering the above cases, the above equation can be generalised as-

 \({{\rm{p}}_{{\rm{ex}}}}{\rm{ = }}\left( {{{\rm{p}}_{{\rm{in}}}}{\rm{ \pm dp}}} \right)\)

Such processes are called reversible processes in which the process could, at any moment, be reversed by an infinitesimal change. The processes that are not reversible are known as irreversible processes. We can relate work to the internal pressure of the system as follows:

\({{\text{w}}_{{\text{rev}}}} = \, – \int\limits_{{{\text{V}}_{\text{i}}}}^{{{\text{V}}_{\text{f}}}} {{{\text{p}}_{{\text{ex}}}}{\text{dV}}} = \, – \,\int\limits_{{{\text{V}}_{\text{i}}}}^{{{\text{V}}_{\text{f}}}} {\left( {{{\text{p}}_{{\text{in}}}} \pm {\text{dp}}} \right){\text{dV}}} \)

Since, \({\rm{dp \times dV}}\) is very small, we can write-

\({{\text{w}}_{{\text{rev}}}} = \, – \int\limits_{{{\text{V}}_{\text{i}}}}^{{{\text{V}}_{\text{f}}}} {{{\text{p}}_{{\text{in}}}}{\text{dV}}} \)

Now, the pressure of the gas (\(\left( {{{\rm{p}}_{{\rm{in }}}}} \right)\) which can be written as \({\text{p}}\) now) can be expressed in terms of its volume through the ideal gas equation. 

For \({\rm{n}}\) mol of an ideal gas, i.e., the ideal gas equation is given by –

\({\rm{pV = nRT}}\)

Therefore, at constant temperature (isothermal process),

\({{\rm{w}}_{{\rm{rev}}}}{\rm{ = \, – }}\int_{{{\rm{V}}_{\rm{i}}}}^{{{\rm{V}}_{\rm{f}}}} {\rm{n}} {\rm{RT}}\frac{{{\rm{dV}}}}{{\rm{V}}}{\rm{ = \,- nRT\,ln}}\frac{{{{\rm{V}}_{\rm{f}}}}}{{{{\rm{V}}_{\rm{i}}}}}{\rm{ = \, – 2}}{\rm{.303\,nR}}\,{\rm{Tlog}}\,\frac{{{{\rm{V}}_{\rm{f}}}}}{{{{\rm{V}}_{\rm{i}}}}}\)

Expansion

Expansion of gas in a vacuum where \({{\rm{p}}_{{\rm{ex}}}}{\rm{ = 0}}\) is called expansion. Whether the process is reversible or irreversible, no work is done during the expansion of an ideal gas.

Let us substitute \({\rm{w = \, – }}{{\rm{p}}_{{\rm{ex}}}}\,\Delta {\text{V}}\) in \({\rm{\Delta U = q + w}}\) and we get-

\({\rm{\Delta U = q – }}{{\rm{p}}_{{\rm{ex}}}}{\rm{\Delta V}}\)

When a process is carried out at constant volume \({\rm{(\Delta V = 0),}}\) then \(\Delta {\text{U = }}{{\text{q}}_{\text{v}}}\) the subscript \({\text{V}}\) in \({{\text{q}}_{\text{v}}}\) implies that heat is supplied at a constant volume.

For isothermal (\({\rm{T = }}\) constant) expansion of an ideal gas into vacuum; \({\rm{w = 0}}\) because \({{\rm{p}}_{{\rm{ex}}}}{\rm{ = 0}}{\rm{.}}\) For isothermal irreversible and reversible changes, \({\rm{\Delta U = q + w}}\) can be stated as follows:

For irreversible isothermal change:

\({\rm{q = \,- w = }}{{\rm{p}}_{{\rm{ex}}}}\left( {{{\rm{V}}_{\rm{f}}}{\rm{ – }}{{\rm{V}}_{\rm{i}}}} \right)\)

For isothermal reversible change:

\({\rm{q = \, – w = nRT}}\,{\rm{ln}}\frac{{{{\rm{V}}_{\rm{f}}}}}{{{{\rm{V}}_{\rm{i}}}}}\)

\({\rm{ = 2}}{\rm{.303\,nRT}}\,{\rm{log}}\frac{{{{\rm{V}}_{\rm{f}}}}}{{{{\rm{V}}_{\rm{i}}}}}\)

For adiabatic change, \({\rm{q = 0}}\)

\({\rm{\Delta U = }}{{\rm{w}}_{{\rm{ad}}}}\)

Summary

Work is a form of energy, and in thermodynamics, it is the energy transferred by the system to its surroundings. It is measured in joules \(\left( {\rm{J}} \right).\) The internal energy of a system reduces when it works on its surroundings. When work is done on a system, the system’s internal energy increases. Expansion of gas in a vacuum where \({{\rm{p}}_{{\rm{ex}}}}{\rm{ = 0}}\) is called expansion. In this article, we have discussed the mechanical work done by a system, i.e. pressure-volume work. We have also discussed the concept of work done by the compression or expansion of a gas.

FAQs

Q.1. What is a SI unit of work?
Ans: The SI unit of work is the same unit as for energy. It is measured in terms of joule \(\left( {\rm{J}} \right).\)

Q.2. What are the applications of thermodynamics in daily life?
Ans: Some of the applications of thermodynamics in daily life include engines that power our motor vehicles, heating and cooling systems in our homes, and the design of buildings and vehicles.

Q.3. Is work scalar or vector?
Ans: Work has magnitude but no direction; hence it is a scalar quantity.

Q.4. What is expansion work?
Ans: The work done as a result of the expansion of the gas is the work of expansion.

Q.5. What is pressure-volume work?
Ans: Pressure-volume work is the work done when there is a change in the volume of the system, provided the external pressure remains constant.

Study About First Law of Thermodynamics Here