Atomic Mass and Composition of Nucleus: Elaboration, Formula, Problems

Introduction:- The nucleus of an atom is present in the central region of an atom where the bulk of the mass is concentrated. By the scattering of alpha particles experiment by Rutherford, we learned that the nucleus of an atom contains a majority of the mass of the atom. It also tells that the nucleus has a positive charge. From the scattering of the \(\alpha\)-particles experiment, the radius of a nucleus is smaller than the radius of an atom by a factor of about \(10^{4}\).

Then, the volume of a nucleus is about \(10^{-12}\) times the volume of the atom. If an atom is amplified to the size of a hall, the size of the nucleus would be like a pinhead. What sort of structure a nucleus has? What are the constituents of the nucleus? How are these held together? In this topic, we are going to answer all of these questions, and we will also discuss various properties of nuclei, such as their size, mass, and stability.

Atomic Mass and Isotopes

The mass of an atom is extremely small; for instance, the mass of a carbon atom, \({ }^{12}C\), is \(1.992647 \times 10^{-26} \mathrm{~kg}\). The kilogram isn’t a convenient unit to measure such small quantities. Therefore, a special mass unit is used to measure the atomic masses. This unit is known as the atomic mass unit (\(u\) or \(amu\)), defined as \(1 / 12\) th of the mass of the carbon \(\left({ }^{12}C\right)\) atom. According to this definition,

\(1 \,\,\text {amu} =\frac{\left.\text { (mass of one } \mathrm{C}^{12} \text { atom }\right)}{12}\)

\(1 \,\,\mathrm{amu}=\frac{1.992647 \times 10^{-26} \mathrm{~kg}}{12}\)

\(1 \,\,\mathrm{amu}=1.660539 \times 10^{-27} \mathrm{~kg}\)

The atomic mass unit (amu) of various elements are close to being integral multiples of the atomic mass of a hydrogen atom. For accurate measurement of atomic masses, we use a mass spectrometer. 

Isotopes elements have the same chemical properties but are different in mass. It happens due to an unequal number of neutrons in the atom. The number of protons (atomic number) is the same in all cases. Let’s take an element has two isotopes having masses \(m_{1} \,a m u\) and \(m_{2}\, a m u\), and the relative abundances of these isotopes are \(\boldsymbol{n}_{1}\) and \(\boldsymbol{n}_{2}\) percent, respectively. Thus, the average mass atom is given by,

\(m=\frac{\left(m_{1} n_{1}+m_{2} n_{2}\right)}{n_{1}+n_{2}}\)

Composition of the Nucleus

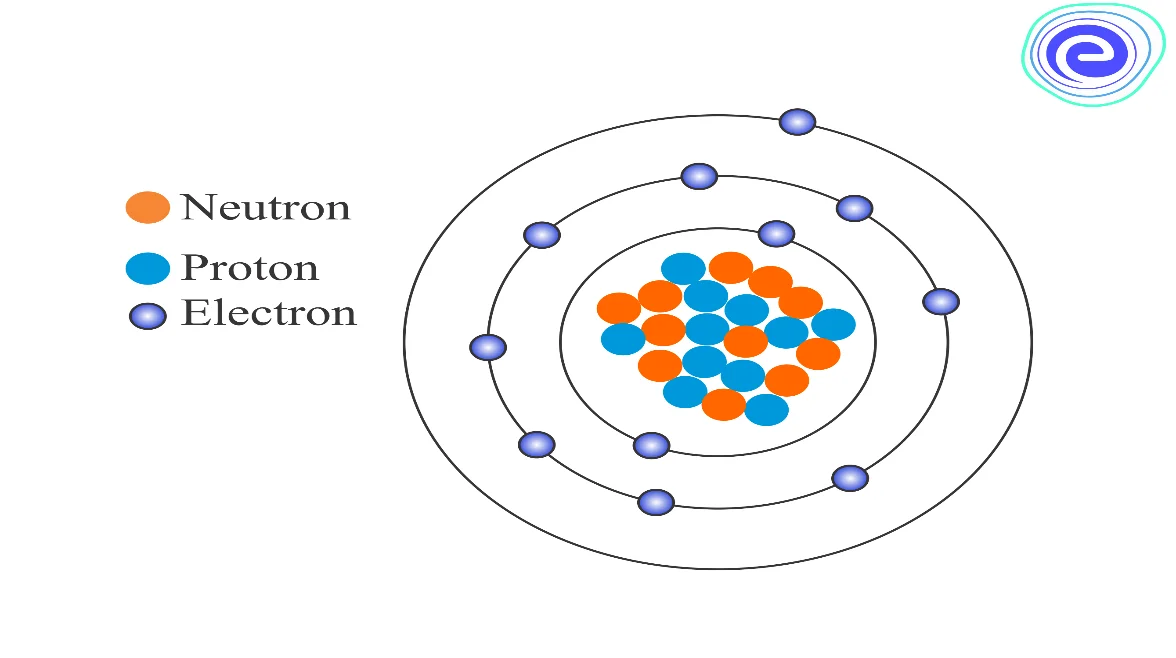
The nucleus of an atom consists of a tightly packed arrangement of protons and neutrons. These are the two heavy particles in an atom, and hence \(99.9\%\) of the mass is concentrated within the nucleus.  Of the two, the protons possess a net positive charge, and hence the nucleus of an atom is positively charged on the entire, and the negatively charged electrons revolve around the central nucleus.

Since the mass concentration at the nucleus of an atom is vast nuclear forces holding the protons and the neutrons together are also large. The protons are concentrated inside the tiny nucleus, and therefore the electrostatic forces of repulsion will also act inside the nucleus. The total number of electrons revolving around the nucleus is equal to the number of protons present inside the nucleus, and hence the atom, on the whole, is electrically neutral.

Let us assume that the atomic number of a neutral atom is \(Z\). The total charge due to electrons is \((-Z e)\), and since the atom is neutral, the charge of the nucleus is \((+Z e)\). The number of protons in the nucleus of the atom is \(Z\). Depending on the isotopes, the number of neutrons \((N)\) may be different for the same atomic number. Based on the above data, we can write, Mass number \((\mathrm{A})=Z+N\)
We use the term nucleon for proton as well as for neutron. Thus, the number of nucleons is equal to the mass number \((A)\) of an atom. Nuclear species or nuclides are shown by the notation \(X_{Z}^{A}\), where \(X\) is the chemical symbol of the species.

Size of the Nucleus

With the help of the Rutherford experiment of scattering of \(\alpha\)-particle by the gold sheet, we can say that the Coulomb repulsive force is only liable for scattering, and it is due to the positively charged proton present inside the nucleus. Rutherford had also estimated that the actual size of the nucleus is of order \(10^{-15} \mathbf{m}(\mathbf{f m})\).
For any atom of mass number \(\boldsymbol{A}\), the radius of the nucleus \((R)\) is given by, \(R=R_{0} A^{\frac{1}{3}}\), where \(R_{0}=1.2 \times 10^{-15} \mathrm{~m}\left(1.2 \,\mathrm{fm} ; 1 \,\mathrm{fm}=10^{-15} \mathrm{~m}\right)\)

Then we can say that the volume of the nucleus, which is proportional to \(\boldsymbol{R}^{3}\) is proportional to \(\boldsymbol{A}\). Thus, the density of the nucleus is constant, independent of \(A\), for all nuclei. The density of the nucleus is close to \(2.3 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3}\), which is extremely larger than ordinary matter, like water, which has a density \(10^{3} \mathrm{~kg} \mathrm{~m}^{-3}\).

Nuclear Force

We know that the protons having a positive charge are present in a very small nucleus. Since the distance between two protons is too small, there will be large repulsion between two protons. Therefore, to bind a nucleus together, there must be an attractive force which strong enough to overcome the repulsion between the protons and to bind both protons and neutrons into the tiny nuclear volume. This force is called nuclear force.

Some features of the nuclear binding force are given below:

(i) The nuclear force is much stronger than the Coulomb force, which acts between charges, or the gravitational force, which acts between masses. 

(ii) The nuclear force between two nucleons falls sharply to zero as their distance is more than a couple of femtometres.

(iii) The nuclear force between neutron-neutron, proton-neutron, and proton-proton is almost the same. The nuclear force doesn’t depend upon the electric charge.

Mass Energy and Nuclear Binding Energy

Einstein showed from his theory of special relativity that it is necessary to treat mass as an equivalent form of energy, and it can be converted into other forms of energy and vice-versa. Einstein gave the mass-energy equivalence relation,

\(E=m c^{2}\)

Here \(m\) is the energy equivalent of mass, and \(c\) is the velocity of light in a vacuum, and it is approximately equal to \(3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}\).

Nuclear Binding Energy

We know that the nucleus contains neutrons and protons. Therefore, the mass of the nucleus should be equal to the total mass of its protons and neutrons. However, the nuclear mass \(\boldsymbol{M}\) will always be less than the sum of the mass of individual protons and neutrons. The difference in mass \(\Delta M\) of a nucleus and its constituents is known as mass defect, and it is given by,

\(\Delta M=\left[Z m_{p}+(A-Z) m_{n}\right]-M\)

Here \(m_{p}\) is the mass of a proton, and \(m_{n}\) is the mass of the neutron.
When a nucleus of a certain charge and mass is formed by bringing together a certain number of neutrons and protons, then energy \(E_{b}\) will be coming out in the process, and it is given by, \(E_{b}=\Delta M c^{2}\). The energy \(E_{b}\) is known as the binding energy of the nucleus. If we try to separate a nucleus into its nucleons, we need to supply total energy equal to \(E_{{b}}\).

Summary

From the Rutherford \(\alpha\)-particles experiment, we get that in every atom, the positive charge, as well as mass, are densely concentrated in the nucleus, and the radius of a nucleus is much smaller than the radius of an atom. The nucleus of an atom consists of protons and neutrons. The electron revolves around the nucleus.

A nucleus of mass number \(\boldsymbol{A}\) has a radius \(R=R_{0} A^{\frac{1}{3}}\), where \(R_{0}=1.2 \times 10^{-15} \mathbf{m}\). When a nucleus of a certain charge and mass is formed by bringing together a certain number of neutrons and protons, then release energy \(\boldsymbol{E}_{b}\) is known as binding energy. The nuclear force which holds nucleons together is much stronger than the Coulomb force, which acts between charges, or the gravitational force, which acts between masses.

Learn Atomic Number and Mass Number

Solved Examples

Q.1. Two stable isotopes of lithium \({ }{3}^{6} \mathrm{Li}\) and \({ }{3}^{7} \mathrm{Li}\) have respective abundances of \(7.5 \%\) and \(92.5 \%\). These isotopes have masses \(6.01512\,{\rm{u}}\) and \(7.01600\,{\rm{u}}\), respectively. Find the atomic mass of lithium.
Ans: Mass of the first lithium isotope \({ }{3}^{6} \mathrm{Li}=\mathrm{m}_{1}=6.01512\,{\rm{u}}\)
Mass of the second lithium isotope \({ }{3}^{7} \mathrm{Li}=\mathrm{m}_{2}=7.01600\,{\rm{u}}\)
Abundance of \({ }{3}^{6} \mathrm{Li}=\mathrm{n}_{1}=7.5 \%\)
Abundance of \({ }{3}^{7} \mathrm{Li}=\mathrm{n}_{2}=92.5 \%\)
The atomic mass \((m)\) of lithium is,
\(m=\frac{\left(m_{1} n_{1}+m_{2} n_{2}\right)}{n_{1}+n_{2}}\)
\(m=\frac{{(6.01512\,{\rm{u}} \times 7.5)+(7.01600\,{\rm{u}} \times 92.5)}}{7.5+92.5}\)
\(m=6.940934\,{\rm{u}}\)
Hence, the atomic mass of lithium is \(6.940934\,{\rm{u}}\).

FAQ on the Atomic Mass and Composition of the Nucleus

Q.1. Write down different isotopes of the hydrogen atom.
Ans: Hydrogen has three isotopes having masses \(1.0078 \,{\rm{u}}, 2.0141 \,{\rm{u}}\), and \(3.0160 \,{\rm{u}}\). The other two isotopes of hydrogen are called Deuterium, \(H_{1}^{2}\) and Tritium, \(H_{1}^{3}\).

Q.2. What are isobars? Explain with examples.
Ans: Isobars that contain the same number of protons but differ from each other in their number of neutrons. Examples: \({ }{1}^{3} H\) and \({ }{2}^{3} H\).

Q.3. What are isotones explain with examples?
Ans: Nuclides with the same neutron number \(N\) but different atomic number \(Z\) are called isotones for example \(H g_{80}^{198}\) and \(A u_{79}^{197}\).

Q.4. Write down the Einstein equation of mass-energy equivalence relation.
Ans: Einstein gave the famous mass-energy equivalence relation,
\(E=m c^{2}\)
Here \(m\) is the energy equivalent of mass, and \(c\) is the velocity of light in a vacuum, and it is approximately equal to \(3 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}\).

Q.5. What is binding energy?
Ans: When a nucleus of a certain charge and mass is formed by bringing together a certain number of neutrons and protons, then released energy \(\boldsymbol{E}_{b}\) is known as binding energy.