Behaviour of Real Gases: Deviations from Ideal Gas Law Behavior

Behaviour of Real Gases: All the gases are examples of real gases. Although no ideal gas exists, real gases are known to show ideal behaviour under certain conditions. Some of the examples of real gases are nitrogen, oxygen, hydrogen, carbon dioxide, helium, etc. In this article, we will study the behaviour of real gases in detail.

Ideal Gas and Real Gas

At all pressures and temperatures, an ideal gas obeys the ideal gas equation \({\rm{PV}} = {\rm{nRT}}.\) No gas, however, is ideal. Almost all gases deviate from the ideal behaviour in some way. Non-ideal or real gases are those that do not obey the ideal-gas equation, such as \({{\rm{H}}_2},\,{{\rm{N}}_2}\) and \({\rm{C}}{{\rm{O}}_2}.\)

Compressibility Factor

The degree to which real gas deviates from ideal behaviour can be expressed using a new function called the Compressibility factor, indicated by \({\rm{Z}}.\) It is defined as

\({\rm{Z = }}\frac{{{\rm{PV}}}}{{{\rm{RT}}}}\)

The degree of deviation from ideal behaviour can be determined by plotting the compressibility factor, \({\rm{Z}},\) vs. \({\rm{P}}.\) An ideal gas has a \({\rm{Z}}\) value of \(1\) and is unaffected by temperature or pressure. The difference between ideal and real gas behaviour is determined by the value of \({\rm{Z}}\) is more or less than \(1.\) The difference between unity and \({\rm{Z}}\) represents the degree of gas nonideality. In a real gas, deviations from ideal behaviour are affected by pressure and temperature. Examining the compressibility curves of some of the gases discussed below as pressure and temperature change will demonstrate this.

Effect of Pressure Variation on Deviations

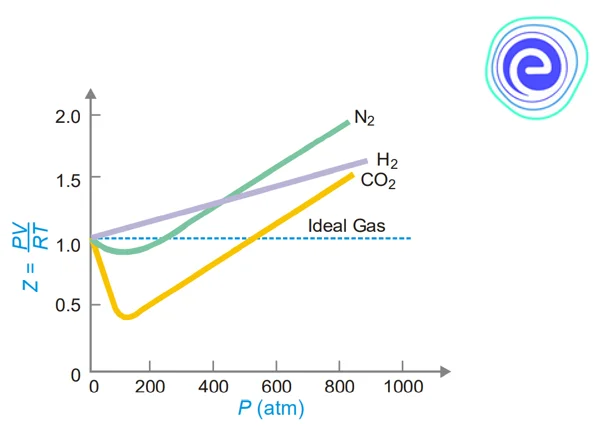
The compressibility factor, \({\rm{Z}},\) for \({{\rm{H}}_2},\,{{\rm{N}}_2}\) and \({\rm{C}}{{\rm{O}}_2}\) at a constant temperature is plotted against pressure in the graph below.

\({\rm{Z}}\) is essentially equal to one at very low pressure for all of these gases. At low pressures, real gases behave almost ideally (up to \(10\) atm). \({{\rm{H}}_2}\) has a constant increase in \({\rm{Z}}\) (from \({\rm{Z}} = 1\)) as the pressure rises. As a result, at all pressures, the \({{\rm{H}}_2}\) curve is higher than the ideal gas curve. For \({{\rm{N}}_2}\) and \({\rm{C}}{{\rm{O}}_2},\,{\rm{Z}}\) declines at first \(\left( {{\rm{Z < }}{\mkern 1mu} 1} \right),\) then passes through a minimum, and then continues to increase with increasing pressure \(\left( {{\rm{Z}} > 1} \right).\) Because \({\rm{C}}{{\rm{O}}_2}\) is the most easily liquefied gas, the dip in the curve is the highest.

Effect of Temperature on Deviations

Plots of \({\rm{Z}}\) or \({\rm{PV}}/{\rm{RT}}\) against \({\rm{P}}\) for \({{\rm{N}}_2}\) at various temperatures are shown in the graph below.

The shape of the graphs shows that as the temperature rises, the deviations from ideal gas behaviour get smaller and smaller. The dip in the curve is substantial at lower temperatures, and the slope of the curve is negative. \({\rm{Z}} < 1\) in this case. The dip in the curve reduces as the temperature rises. The minimum in the curve disappears at a specific temperature and remains horizontal for a significant range of pressures. \({\rm{PV}}/{\rm{RT}}\) is almost unity at this temperature, and Boyle’s law is fulfilled. Hence, this temperature of the gas is known as Boyle’s temperature. The Boyle temperature of each gas is unique, for example, \(332\,{\rm{K}}\) for \({{\rm{N}}_2}.\)

Conclusions

On the basis of the above study, we can conclude that:

1. At low pressures and relatively high temperatures, real gases behave nearly ideal, and the ideal-gas equation is obeyed.
2. At low temperatures and sufficiently high pressures, a real gas deviates significantly from ideality, and the ideal-gas equation is no longer applicable.
3. The deviation from ideal behaviour increases as the gas gets closer to the liquefaction point.

Explanation of Deviations – Van der Waals Equation (Causes of Real Gas Behaviour)

The departures of real gases from ideal behaviour, according to Van der Waals \(\left( {1873} \right),\) are due to two kinetic theory postulates that are incorrect. These are the following:

1. The molecules in a gas have no volume and are point masses.
2. In a gas, there are no intermolecular attractions.

As a result, the kinetic theory-derived ideal gas equation \({\rm{PV}} = {\rm{nRT}}\) could not be applied to real gases. To make the ideal gas equation applicable to real gases, Van der Waals pointed out that the equation’s pressure \(\left( {\rm{P}} \right)\) and volume \(\left( {\rm{V}} \right)\) elements needed to be corrected.

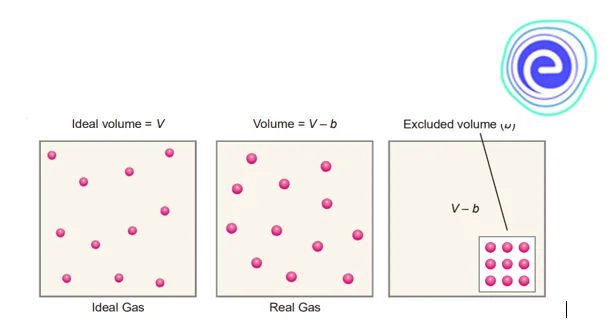
Volume Correction

The open space in the container in which molecules move around is the volume of a gas. The volume \({\rm{V}}\) of an ideal gas is the same as the container’s volume. Ideal gas molecules have no volume; therefore, they can travel around the container as much as they like. Van der Waals, on the other hand, considered that molecules in a real gas are rigid spherical objects with a defined volume.

As a result, the volume of a real gas is ideal volume less the volume occupied by gas molecules. The volume in the ideal gas equation is rectified as follows if \({\rm{b}}\) is the effective volume of molecules per mole of gas:

\(\left( {{\rm{V}} – {\rm{b}}} \right)\)

For n moles of the gas, it becomes,

\(\left( {{\rm{V}} – {\rm{nb}}} \right)\)

Where,

\({\rm{b}}\) stands for the excluded volume, which is constant and unique to each gas.

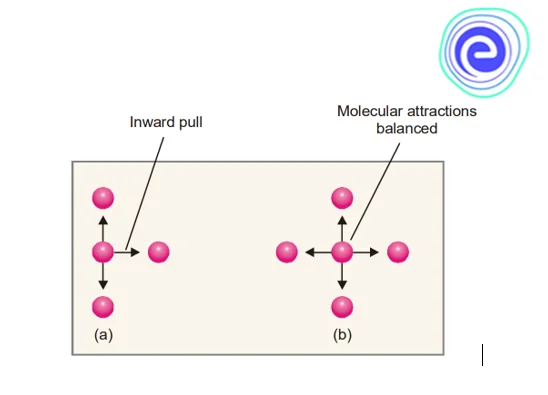
Pressure Correction

Other molecules on all sides attract a molecule in the interior of a gas. These attractive factors cancel each other out. However, a molecule poised to strike the vessel’s wall is only drawn by molecules on one side. As a result, it feels compelled to turn inside. As a result, it hits the wall at a lower velocity, and the real gas pressure, \({\rm{P}},\) is lower than the ideal pressure. If the actual pressure \({\rm{P}}\) is less than \({{\rm{P}}_{{\rm{ideal}}}}\) by a quantity \({\rm{p}},\) we have

\({\rm{P}} = {{\rm{P}}_{{\rm{ideal}}}} – {\rm{p}}\)

\({{\rm{P}}_{{\rm{ideal}}}} = {\rm{P}} + {\rm{p}}\)

The value of quantity \({\rm{p}}\) has been given by Van der Waals as:

\({\rm{p}} = \frac{{{\rm{a}}{{\rm{n}}^2}}}{{{{\rm{V}}^2}}}\)

Where \({\rm{n}}\) is the total number of gas molecules in volume \({\rm{V}},\) and a is the proportionality constant characteristic of the gas. Thus, the pressure \({\rm{P}}\) in the ideal gas equation is corrected as:

\(\left( {{\rm{P}} + \frac{{{\rm{a}}{{\rm{n}}^2}}}{{{{\rm{V}}^2}}}} \right)\)

for \({\rm{n}}\) moles of gas.

Substituting the values of corrected pressure and volume in the ideal gas equation, \({\rm{PV}} = {\rm{nRT}},\) we have:

\(\left( {{\rm{p}} + \frac{{{\rm{a}}{{\rm{n}}^{\rm{2}}}}}{{{{\rm{V}}^{\rm{2}}}}}} \right)\left( {{\rm{V}} – {\rm{nb}}} \right) = {\rm{nRT}}\)

This is known as the Van der Waals equation or real gas equation for \({\rm{n}}\) moles of a gas. For \(1\) mole of gas \(\left( {{\rm{n}} = 1} \right),\) the Van der Waals equation becomes:

\(\left( {{\rm{p}} + \frac{{\rm{a}}}{{{{\rm{V}}^{\rm{2}}}}}} \right)\left( {{\rm{V}} – {\rm{b}}} \right) = {\rm{RT}}\)

Constant \({\rm{a}}\) and \({\rm{b}}\) are called van der Waals constants. These constants are unique to each type of gas.

Summary

1. At all pressures and temperatures, an ideal gas obeys the ideal gas equation \({\rm{PV}} = {\rm{nRT}}.\)
2. No gas, however, is ideal. Almost all gases deviate from the ideal behaviour in some way. Non-ideal or real gases are the terms used to describe them.
3. The extent to which real gas deviates from ideal behaviour can be expressed using a new function known as the Compressibility factor.
4. As a result, the kinetic theory-derived ideal gas equation \({\rm{PV}} = {\rm{nRT}}\) could not be applied to real gases.
5. At low pressures and relatively high temperatures, real gases behave nearly ideal, and the ideal-gas equation is obeyed.
6. At low temperatures and sufficiently high pressures, a real gas deviates significantly from ideality, and the ideal-gas equation is no longer applicable.
7. The ideal gas equation was modified by Van der Waals to make it applicable to all gases. This equation is known as the Van der Waals equation and is given below for \({\rm{n}}\) moles of gases.
   \(\left( {{\rm{p}} + \frac{{{\rm{a}}{{\rm{n}}^{\rm{2}}}}}{{{{\rm{V}}^{\rm{2}}}}}} \right)\left( {{\rm{V}} – {\rm{nb}}} \right) = {\rm{nRT}}\)

FAQs on Behaviour of Real Gases

Q.1. Define ideal gas and real gas.
Ans: At all pressures and temperatures, an ideal gas obeys the ideal gas equation \({\rm{PV}} = {\rm{nRT}}.\) No gas, however, is ideal. Almost all gases deviate from the ideal behaviour in some way. Non-ideal or real gases are those that do not obey the ideal-gas equation, such as \({{\rm{H}}_2},\,{{\rm{N}}_2}\) and \({\rm{C}}{{\rm{O}}_2}.\)

Q.3. What is the ideal behaviour of gases?
Ans: At all pressures and temperatures, an ideal gas obeys the ideal gas equation \({\rm{PV}} = {\rm{nRT}}.\) No gas, however, is perfect. Almost all gases deviate from the ideal behaviour in some way.

Q.2. What is the compressibility factor?
Ans: The extent of deviation of real gas from ideal behaviour may be depicted in terms of a new function called the Compressibility factor, denoted by \({\rm{Z}}.\) It is defined as
\({\rm{Z = }}\frac{{{\rm{PV}}}}{{{\rm{RT}}}}\)

Q.4. What is the behaviour of real gases?
Ans: Real gases are gases that deviate from ideal behaviour. The extent of deviation of real gas from ideal behaviour may be depicted in terms of a new function called the Compressibility factor, denoted by \({\rm{Z}}.\) It is defined as
\({\rm{Z = }}\frac{{{\rm{PV}}}}{{{\rm{RT}}}}\)
The extent of deviation from ideal behaviour may be shown by a plot of the compressibility factor, \({\rm{Z}},\) against \({\rm{P}}.\) For an ideal gas, \({\rm{Z}} = 1,\) and it is independent of temperature and pressure.

Q.5. What are the causes of real gas behaviour? Derive Van der Waals Equation.
Ans: The departures of real gases from ideal behaviour, according to Van der Waals \(\left( {1873} \right),\) are due to two kinetic theory postulates that are incorrect. These are the following:
1. The molecules in a gas have no volume and are point masses.
2. In a gas, there are no intermolecular attractions.
As a result, the kinetic theory-derived ideal gas equation \({\rm{PV}} = {\rm{nRT}}\) could not be applied to real gases. To make the ideal gas equation applicable to real gases, Van der Waals pointed out that both the pressure \(\left( {\rm{P}} \right)\) and volume \(\left( {\rm{V}} \right)\) elements in the equation needed to be corrected.
The ideal gas equation was modified by Van der Waals to make it applicable to all gases. This equation is known as the Van der Waals equation and is given below for n moles of gases.
\(\left( {{\rm{p}} + \frac{{{\rm{a}}{{\rm{n}}^{\rm{2}}}}}{{{{\rm{V}}^{\rm{2}}}}}} \right)\left( {{\rm{V}} – {\rm{nb}}} \right) = {\rm{nRT}}\)

Study Diffusion of Gases Concept Here