Composition of Functions: Definition, Formula, Examples

Composition of functions: When we perform algebraic operations on functions, it results in a new function. In a similar way, we can create new functions by composing functions. When we have to compute the heating cost from a day of the year, we create a new function that takes a day as its input and yields the cost as output. When the output of one function acts as the input of another, it is known as a composition of functions. A composite function is generally written as a function written inside another function. Let us learn about the composition of functions in detail.

What is a Composite Function?

Suppose we have two different functions say \(f(x)\) and \(g(x),\) then we can combine them to create a new function by composing one function (say \(g(x)\)) into the other (say \(f(x)\)). The steps followed to perform this operation are similar to those required to solve any function for any given value. Such functions are referred to as composite functions. The operation is called the composition of functions.

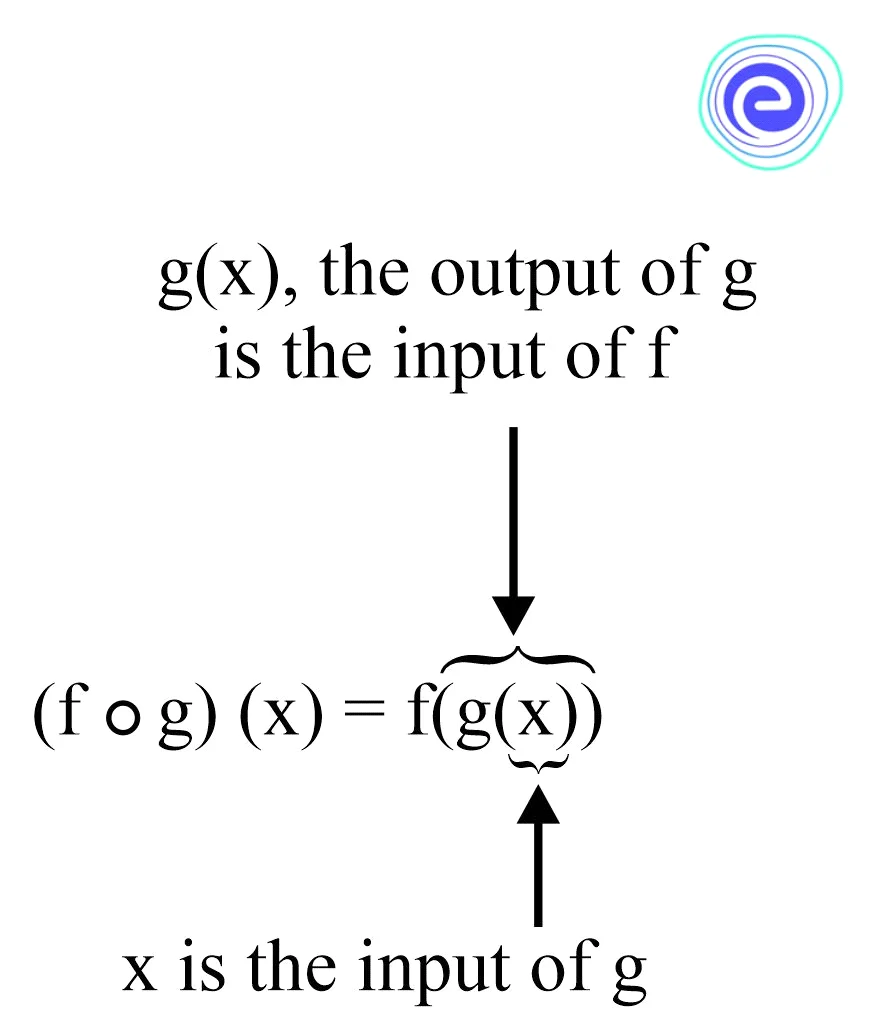
\(f(g(x))\) is a composite function of \(f(x)\) and \(g(x).\) The resulting function is known as the composite function. We represent this composition by the notation 

\((f \circ g)(x) = f(g(x))\)

In general, a composite function is a function written inside another function. The composition of a function is a mathematical operation where two functions say \(f\) and \(g\) generate a new function say \(ℎ,\) in such a way that \(h(x) = g(f(x)).\) It means that function \(g\) is applied to the function of \(f.\) So, a function is applied to the result of another function.

Representation of Composite Functions

The composition of the function is denoted as \((g \circ f)\left( x \right),\) where \( \circ \) is a small circle symbol called the composition operator. We cannot replace the operator with a dot \((∙)\) because it will show as the product of two functions, such as \((g \cdot f)(x).\) We use this operator when we wish to emphasize the relationship between the functions themselves without referring to any particular input value.

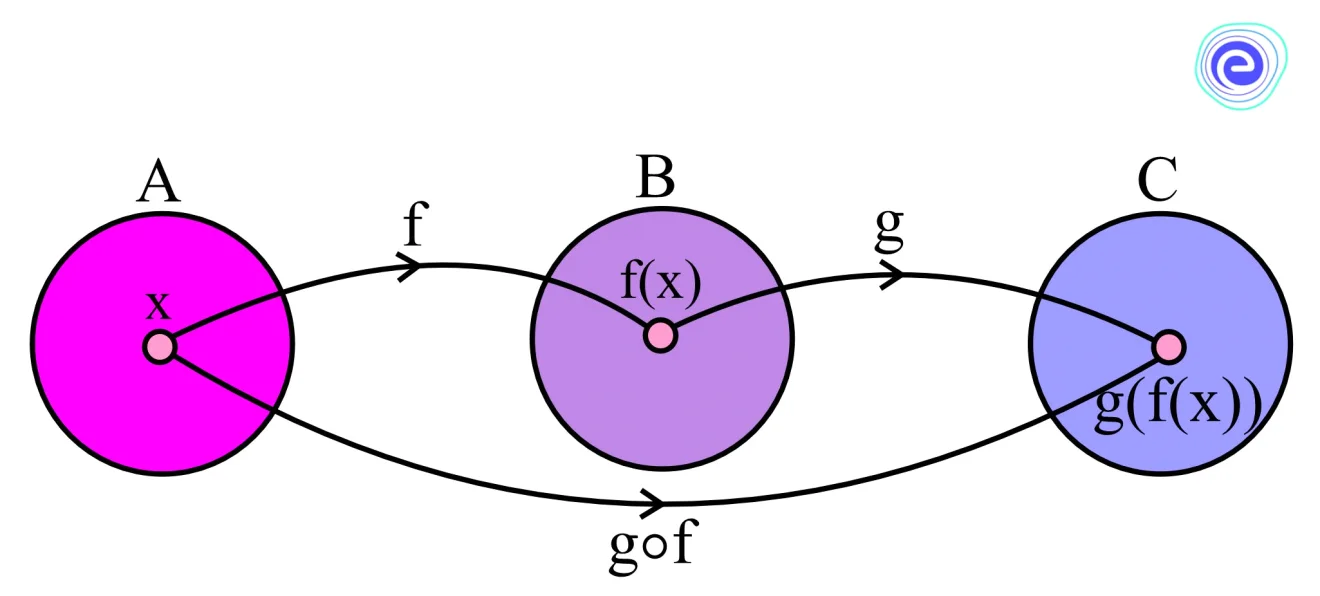
Consider two functions, \(f:A⟶B\) and \(g:B⟶C.\) Then, the composition of \(f\) and \(g,\) denoted by \(g \circ f\) is defined as the function \((g \circ f)(x) = g(f(x))\) for all \(x∈A.\)

Composition as an Operation

Complicated functions can be built from simple functions by using composition. In composition process, the output of one function is given as input to another function. This means that an input \(x\) is given to \(f(x),\) and the output is given as input to the next function \(g.\)

The order of function is an important factor while dealing with the composition of functions since the composition of functions is not commutative. This can be represented as 

\((f\circ g)(x) \ne (g\circ f)(x)\)

Composition is a simple yet powerful operation that takes two functions with one function as the argument for the other and forms a new function. It is much similar to addition or multiplication that takes two numbers and gives their sum or product as the output, which is new number. But, it is very important not to get confused with the function composition with multiplication. Because, in most cases, \(f(g(x)) \ne f(x)g(x).\)

Domain and Range

The domain of a function is a set of all values, the set of \(x\) values which go into the function \(f(x).\) In the composition of \((f\circ g)(x)\) the domain of the function \(f\) is also the domain of \(g(x).\)

We cannot simply compose any two random functions. Some functions cannot be composed together. For example, let’s say \(f(x) = \ln (x)\) and \(g(x) = – {x^2}.\) If we try to compose \(f(g(x)),\) it is not possible as the logarithmic function cannot take negative input values, so \(f(g(x))\) is not possible.

In another case, suppose \(f(x) = \sqrt x \) and \(g(x) = \log (x).\) In this case, the domain of \(f(x)\) is positive real numbers. Here, for \(f(g(x)),\) we need to make sure that \(\log (x)\) does not give negative values as the outputs. So, the range of \(f(x)\) must lie within the domain of \(g(x).\) 

Some pairs of functions cannot make a composite function. For some other pair of functions, the domains can be modified. In such cases, the following must be noted: 

1. In the case of \(f(g(x)),\) the range of \(g(x)\) must lie inside the domain of \(f(x).\)
2. If not, the domain of \(g(x)\) should be modified such that the range of \(g(x)\) lies inside the domain of \(f(x).\)

The domain of the composite function is either same as the domain of the first function or lies inside it. The range of the composed function is either the same as the range of the second function or the function lies inside it. 

Properties of the Composition of Functions

Associative Property

If there are three functions \(f, g\) and \(ℎ,\) then they are said to be associative if and only if

\(f\circ (g\circ h) = (f\circ g)\circ h\)

Proof

We have \(h\circ (g\circ f)(x) = h(g\circ f(x)) = h(g(f(x))),\forall x\) and

\((h\circ g)\circ f(x) = h\circ g(f(x)) = h(g(f(x))),\forall x\) in \(X\)  

Hence, \(h\circ (g\circ f) = (h\circ g)\circ f.\) 

Commutative Property

Two functions \(f\) and \(g\) are said to be commutative with each other, if and only if

\(g\circ f = f\circ g\)

The composition function of a one-to-one function is always one to one.

The composition function of two onto functions is always onto

For two functions \(f\) and \(g,\) the inverse of their composition is equal to the composition of the inverse of the functions in reverse order. It is represented as

\({(f\circ g)^{ – 1}} = {g^{ – 1}}\circ {f^{ – 1}}\)

Proof

To show that \(g \circ f\) is invertible with \({(g\circ f)^{ – 1}} = {f^{ – 1}}\circ {g^{ – 1}},\) it is enough to show that \(\left. {\left( {{f^{ – 1}}\circ } \right.{g^{ – 1}}} \right)\circ (g\circ f) = {I_X}\) and \((g\circ f)\circ \left( {{f^{ – 1}}\circ {g^{ – 1}}} \right) = {I_Z}.\) 

Now, that \(\left. {\left( {{f^{ – 1}}\circ {g^{ – 1}}} \right)\circ (g\circ f) = \left( {\left( {{f^{ – 1}}\circ {g^{ – 1}}} \right)\circ g} \right)\circ f} \right),\) by Associtivity Theorem

\( = \left( {{f^{ – 1}} \circ \left( {{g^{ – 1}} \circ g} \right) \circ f} \right)\) by Associtivity Theorem 

\( = \left( {{f^{ – 1}}\circ {I_Y}} \right)\) of, by definition of \({{g^{ – 1}}}\) 

\( = {I_X}\) 

Similarly, it can be shown that \((g\circ f)\circ \left( {{f^{ – 1}}\circ {g^{ – 1}}} \right) = {I_Z}\)

Composition of a Function by Itself

Similar to the way we compose two functions, we can compose a function with itself.  Suppose \(f\) is a function, then the composition of function \(f\) with itself will be

\((f\circ f)(x) = f(f(x))\)

Solved Examples on a Composition of Functions

Q.1. Consider the function \(f(x)=2x+3.\) Find \((f \circ f)(x).\)

Sol: Given function is \(f(x)=2x+3\)

\((f\circ f)(x) = f(f(x))\) 

\(=2(2x+3)+3\)

\(=4x+9\) 

Q.2. Find \((g∘f)(x)\) given that \(f(x)=2x+3\) and \(g (x)= –x^2+5.\)

Sol:  The composition of a function can be obtained by \((g∘f)(x)=g(f(x))\)

Replace \(x\) in \(g(x) = – {x^2} + 5\) with \(2x+3\)
\( = \, – (2x + 3)2 + 5\)

\( = \,- \left( {4{x^2} + 12x + 9} \right) + 5\)

\( = \, – 4{x^2} – 12x – 9 + 5\)

\( = \, – 4{x^2} – 12x – 4\)

Q.3. Evaluate \(f(g(6))\) for the functions \(f(x) = 5x + 4\) and \(g(x) = x – 3.\)

Sol: To find the value of \(f(g(6)),\) first, find the value of \(f(g(x)).\)

\( \Rightarrow f(g(x)) = 5(x – 3) + 4\) 

\( = 5x – 15 + 4\) 

\( = 5x – 11\)

Now substitute \(x\) in \(f(g(x))\) with \(6\)

\( \Rightarrow 5x – 11 = 5(6) – 11\)

\( \Rightarrow 30 – 11\) 

\( = 19\)

Therefore, \(f(g(6)) = 19\)

Q.4. Find \(f(g (5))\) given that \(f(x)=4x+3\) and \(g(x)=x–2.\)

Sol: To find the value of \(f(g(6))\) first, find the value of \(f(g(x)).\)

\(⇒f(x)=4x+3 \)

\(⇒g(x)=x–2\)

\(f(g(x))=4(x–2)+3\) 

\(=4x–8+3\)

\(=4x−5\)

Now, we can find the value of \(f(g(5))\) by substituting \(x\) in \(f(g(x))\) with \(5.\)

\(f(g (5))=4(5)–5\)

\(=20−5\)

\(∴f(g (5))=15\)

Q.5. Given \(g(x)=2x+8\) and \(f(x) = 8{x^2},\) Find \(\left( {f \circ g} \right)\left( x \right)\)

Sol: The composition of functions can be found by

\((f\circ g)(x) = f(g(x))\) 

Replace \(x\) in \(f(x) = 8{x^2}\) with \((2x+8)\)

\( \Rightarrow (f\circ g)(x) = f(g(x)) = 8{(2x + 8)^2}\) 

\( \Rightarrow (f\circ g)(x) = 8\left[ {4{x^2} + {8^2} + 2(2x)(8)} \right]\) 

\( \Rightarrow (f\circ g)(x) = 8\left[ {4{x^2} + 64 + 32x} \right]\) 

\( \Rightarrow (f\circ g)(x) = 32{x^2} + 512 + 256x\) 

\( \Rightarrow (f\circ g)(x) = 32{x^2} + 256x + 512\) 

Summary

Function composition is a mathematical operation that takes two functions, \(f\) and \(g,\) and produces a new function, say \(ℎ=g∘f,\) such that \(ℎ(x)=g(f(x)).\) The composition of a function is accomplished by substituting the output of one function as input to another. We can also compose a function with itself, the same way we are composing two different functions. The composition of functions is both associative and commutative. In the case of \(f(g(x)),\) the range of \(g(x)\) must lie inside the domain of \(f(x).\) If not, the domain of \(g(x)\) should be modified such that the range of \(g(x)\) lies inside the domain of \(f(x).\)

FAQs on Composition of Functions

The frequently asked questions on composition of functions are given below:

Q.1. How to do the composition of two functions?
Ans: The composition of a function is accomplished by substituting one function for another. Let \(f:A⟶B\) and \(g:B⟶C\) be two functions. Then the composition of \(f\) and \(g\) denoted by \(g \circ f\) is defined as the function \(g \circ f\left( x \right) = g\left( {f\left( x \right)} \right)\) for all \(x∈A.\)

Q.2. What is the composition of functions?
Ans: Function composition is a mathematical operation that takes two functions, \(f\) and \(g\), and produces a function \(ℎ=g∘f\) such that \(ℎ(x)=g(f(x)).\) The function \(g\) is applied to the result of applying the function \(f\) to \(x\) in this operation.

Q.3. Is the composition of functions associative?
Ans: Yes, the composition of functions is associative. If there are three functions \(f, g\) and \(ℎ,\) they are associative if and only if \(f∘(g∘ℎ)=(f∘g)∘ℎ.\)

Q.4. What is the composition of functions in terms of their inputs and outputs?
Ans: The application of one function to the result of another function is known as function composition. A function’s input is the value on which the function is performed. The result of the function operations performed on the independent variable is the function’s output. If the composition of a function is \(f(g(x)),\) then \(g(x)\) is the input and \(f(g(x))\) is the output.

Q.5. What is the domain of a composite function?
Ans: The domain of a composite function \(f(g(x))\) is the set of those inputs \(x\) in the domain of \(g\) for which \(g(x)\) is in the domain of \(f.\)
The composition of two functions occurs when one function is evaluated in terms of another function, with the range of the first function determining the domain of the second function.