Determinants: Definition, Finding Determinant of Square Matrix

The determinants aid in the discovery of a matrix’s adjoint, or inverse. We must also use the notion of determinants to solve linear equations using the matrix inversion approach. Calculating determinants makes it simple to recall the cross-product of two vectors. Determinants are expressed in the same way as matrices, but with the addition of a modulus sign. Let’s learn more about determinants, their characteristics, the rules for finding determinants of various orders, and how to compute them with solved examples in this article.

What are Determinants?

Determinants are scalar quantities calculated by adding the sums of the products of the elements of a square matrix according to a set of rules. 

Every square matrix has a determinant, which is an expression or a number that may be connected with it.

If \(A = \left[ {{a_{ij}}} \right]\) is a square matrix of order \(n,\) then the determinant of \(A\) is denoted by det \(A\) or \(|A|,\) and can be written as,

\(\left| {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1j}}}& \cdots &{{a_{1nn}}} \\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2j}}}& \cdots &{{a_{2n}}} \\ \vdots & \vdots &{}& \vdots &{}& \vdots \\ {{a_{i1}}}&{{a_{i2}}}& \cdots &{{a_{ij}}}& \cdots &{{a_{in}}} \\ \vdots & \vdots &{}& \vdots &{}& \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nj}}}& \cdots &{{a_{nn}}} \end{array}} \right|\)

Learn about the Types of Matrices here

Determinant of a First-order Square Matrix

If \(A = \left[ {{a_{11}}} \right]\) is a square matrix of order \(1,\) then the determinant of \(A\) is written as \(|A| = {a_{11}},\) or \(\left| {{a_{11}}} \right| = {a_{11}}.\)

Determinant of a Second-order Square Matrix

If \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}} \\ {{a_{21}}}&{{a_{22}}} \end{array}} \right]\) is a square matrix of order \(2,\) then the expression \({a_{11}}{a_{22}} – {a_{21}}{a_{12}}\) is the determinant of \(A.\)

i.e., \(|A| = \left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}} \\ {{a_{21}}}&{{a_{22}}} \end{array}} \right| = {a_{11}}{a_{22}} – {a_{21}}{a_{12}}…….\left( i \right)\)

Thus, the product of diagonal elements minus the product of off-diagonal elements equals the determinant of a square matrix of order \(2.\)

Determinant of a Third-order Square Matrix

If \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]\) is a square matrix of order \(3,\) then the determinant of \(A\) is defined as,

\({a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{13}}{a_{32}}{a_{21}} – {a_{11}}{a_{23}}{a_{32}} – {a_{22}}{a_{13}}{a_{31}} – {a_{12}}{a_{21}}{a_{33}}\)

i.e.,

\(|A| = \left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right|\)
\( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{13}}{a_{32}}{a_{21}} – {a_{11}}{a_{23}}{a_{32}} – {a_{22}}{a_{13}}{a_{31}} – {a_{12}}{a_{21}}{a_{33}}……\left( {ii} \right)\)

Or

\(|A| = \left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right|\)

\( = {a_{11}}\left( {{a_{22}}{a_{33}} – {a_{23}}{a_{32}}} \right) – {a_{12}}\left( {{a_{33}}{a_{21}} – {a_{23}}{a_{31}}} \right) + {a_{13}}\left( {{a_{32}}{a_{21}} – {a_{22}}{a_{31}}} \right)\)

\( = {a_{11}}\left| {\begin{array}{*{20}{l}} {{a_{22}}}&{{a_{23}}}\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right| – {a_{12}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {a_{13}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{22}}}\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right|\,\,\,\left[ {{\rm{Using}}\left( i \right)} \right]\)

\(\therefore |A| = {( – 1)^{1 + 1}}{a_{11}}\left| {\begin{array}{*{20}{l}} {{a_{22}}}&{{a_{23}}}\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{1 + 2}}{a_{12}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{1 + 3}}{a_{13}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{22}}}\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right|\)

Thus, the determinant of a square matrix of order \(3\) is the sum of the product of elements \({a_{1j}}\) in first row with \({\left( { – 1} \right)^{1 + j}}\) times the determinant of a \(2 \times 2\) sub-matrix obtained by leaving the first row and the first column the element is present in.

The above expansion of \(A\) is known as the expansion along first row.

There are three rows and three columns in a square matrix of order \(3.\) The expression \(\left( {ii} \right)\) for the determinant of a square matrix of order \(3\) can be arranged in various forms to obtain the expansion of \(\left| A \right|\) along any of its rows or columns. 

In order to expand \(\left| A \right|\) about a row or a column we multiply each element \({a_{ij}}\) in the \({i^{{\text{th}}}}\) row with \({\left( { – 1} \right)^{1 + j}}\) times the determinant of the sub-matrix obtained by leaving the row and column the element in present in.

Consider, \(|A| = \left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right|\)

Along the second row, 

\(|A| = {( – 1)^{2 + 1}}{a_{21}}\left| {\begin{array}{*{20}{l}} {{a_{12}}}&{{a_{13}}}\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{2 + 2}}{a_{22}}\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{13}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{2 + 3}}{a_{23}}\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right|\)

About second column,

\(|A| = {( – 1)^{1 + 2}}{a_{12}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{2 + 2}}{a_{22}}\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{13}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{3 + 2}}{a_{32}}\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{23}}} \end{array}} \right|\)

This method can be used for any row and column to compute \(|A|\) of a square matrix.

Note 1: Determinants are only found for square matrices. There are no determinants for non-square matrices.

Note 2: The determinant of a square matrix of order \(3\) can be expanded along any row or column.

Note 3: If a row or a column of a determinant consists of all zeros, then the value of the determinant is zero.

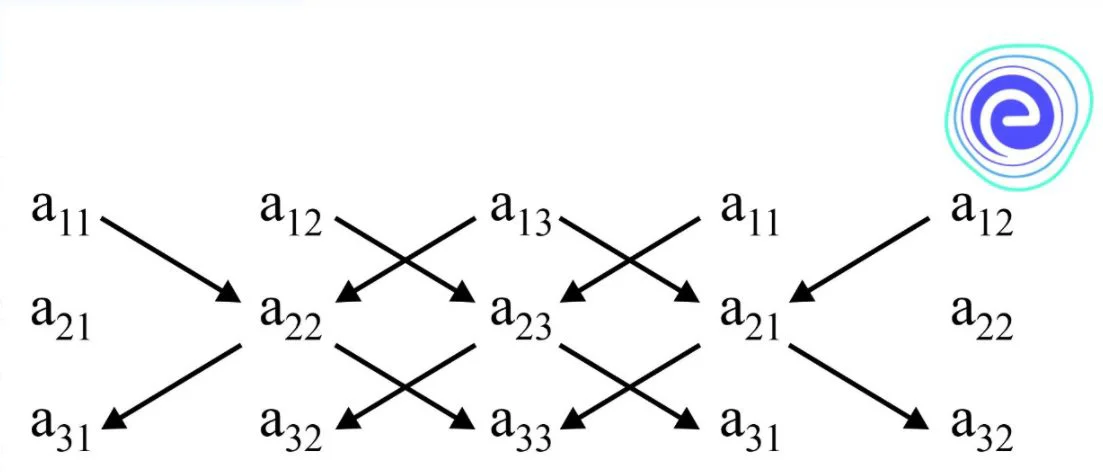
Determinant of a Third Order Square Matrix by Using Sarrus Diagram

The determinant of a square matrix of order \(3\) can be evaluated by the following procedure called the Sarrus diagram.

Consider this determinant \(\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right|\)   of the square matrix \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]\)

In order to find the value of the determinant, follow these steps described below.

Step 1: Enlarge the determinant by adjoining the first two columns on the right.

Step 2: Draw lines parallel and perpendicular to the diagonal as shown below.

Step 3: The required value of the determinant is sum of the product of all elements given diagonally and indicated by right arrow starting from \({{a_{11}}}\) to \({{a_{22}}}\) to \({{a_{33}}},\) then \({{a_{12}}}\) to \({{a_{23}}}\) to \({{a_{31}}},….\) and so on, minus sum of the product of all off-diagonal elements indicated by left arrow and starting from \({{a_{13}}}\) to \({{a_{22}}}\) to \({{a_{31}}}\) then \({{a_{11}}}\) to \({{a_{23}}}\) to \({{a_{32}}},….\) and so on.

Thus, 

\(\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right| = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{13}}{a_{21}}{a_{32}} – {a_{13}}{a_{22}}{a_{31}} – {a_{11}}{a_{23}}{a_{32}} – {a_{12}}{a_{21}}{a_{33}}\)

Note: This method does not work for determinants of order more than \(3.\)

Minors of a Matrix

Let \(A = \left[ {{a_{ij}}} \right]\) be a square matrix of order \(n.\) The minor \({{M_{ij}}}\) of \({{a_{ij}}}\) in \(A\) is the determinant of the square sub-matrix of order \(\left( {n – 1} \right)\) obtained by leaving \({i^{{\text{th}}}}\) row and \({j^{{\text{th}}}}\) column in \(A.\)

Example:

If \(A = \left[ {\begin{array}{*{20}{c}} 4&{ – 7}\\ { – 3}&2 \end{array}} \right]\) then,

\({M_{11}} = Minor\,of\,{a_{11}} = 2\)

\({M_{12}} = Minor\,of\,{a_{12}} = – 3\)

\({M_{21}} = Minor\,of\,{a_{21}} = – 7\)

\({M_{22}} = Minor\,of\,{a_{22}} = 4\)

If \(A = \left[ {\begin{array}{*{20}{c}} 1&2&3\\ { – 3}&2&{ – 1}\\ 2&{ – 4}&3 \end{array}} \right]\) then,

\({M_{11}} = Minor\,of\,{a_{11}} = \)Determinant of the \(2 \times 2\) square sub-matrix obtained by leaving first row and first column of \(A.\)

\( \Rightarrow {M_{11}} = \left| {\begin{array}{{c}} 2 & { – 1}  \\ { – 4} & 3  \\ \end{array} } \right| = 6 – 4 = 2\)

Similarly, 

\({M_{12}} = Minor\,of\,{a_{12}} = \left| {\begin{array}{*{20}{c}} { – 3}&{ – 1}\\ 2&3 \end{array}} \right| = – 9 + 2 = – 7\)

\({M_{13}} = Minor\,of\,{a_{13}} = \left| {\begin{array}{*{20}{c}} { – 3}&2\\ 2&{ – 4} \end{array}} \right| = 12 – 4 = 8\)

\({M_{21}} = Minor\,of\,{a_{21}} = \left| {\begin{array}{*{20}{c}} 2&3\\ { – 4}&3 \end{array}} \right| = 6 + 12 = 18\)

\({M_{22}} = Minor\,of\,{a_{22}} = \left| {\begin{array}{*{20}{l}} 1&3\\ 2&3 \end{array}} \right| = 3 – 6 = – 3\)

\({M_{23}} = Minor\,of\,{a_{23}} = \left| {\begin{array}{*{20}{c}} 1&2\\ 2&{ – 4} \end{array}} \right| = – 4 – 4 = – 8\)

\({M_{31}} = Minor\,of\,{a_{31}} = \left| {\begin{array}{*{20}{c}} 2&3\\ 2&{ – 1} \end{array}} \right| = – 2 – 6 = – 10\)

\({M_{32}} = Minor\,of\,{a_{32}} = \left| {\begin{array}{*{20}{c}} 1&3\\ { – 3}&{ – 1} \end{array}} \right| = – 1 + 9 = 8\)

\({M_{33}} = Minor\,of\,{a_{33}} = \left| {\begin{array}{*{20}{c}} 1&2\\ { – 3}&2 \end{array}} \right| = 2 + 6 = 8\)

Cofactors of a Matrix:

Assume \(A = \left[ {{a_{ij}}} \right]\) to be an n-dimensional square matrix. The cofactor \({{C_{ij}}}\) of \({{a_{ij}}}\) in \(A\) is equal to \({( – 1)^{i + j}}\) times the determinant of the sub-matrix of order \((n – 1)\) produced by leaving \({i^{{\text{th}}}}\) row and \({j^{{\text{th}}}}\) column in \(A.\)

It follows from the definition that,

\({{C_{ij}} = }\)Cofactor of \({{a_{ij}}}\) in \(A = {( – 1)^{i + j}}{M_{ij}},\) where \({{M_{ij}}}\) is the minor of \({{a_{ij}}}\) in \(A.\)

Thus, we have

\({C_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{M_{ij}},{\rm{ if }}\,i + j\,{\rm{ is\, even }}}\\ { – {M_{ij}},{\rm{ if }}\,i + j\,{\rm{ is\, odd }}} \end{array}} \right.\)

Example:

If \(A = \left[ {\begin{array}{*{20}{c}} 4&{ – 7}\\ { – 3}&2 \end{array}} \right]\) then,

\({C_{11}} = {( – 1)^{1 + 1}}{M_{11}} = {M_{11}} = 2\)

\({C_{12}} = {( – 1)^{1 + 2}}{M_{12}} = – {M_{12}} = 3\)

\({C_{21}} = {( – 1)^{2 + 1}}{M_{21}} = – {M_{21}} = – ( – 7) = 7\)

\({C_{22}} = {( – 1)^{2 + 2}}{M_{22}} = 4\)

If \(A = \left[ {\begin{array}{*{20}{c}} 1&2&3\\ { – 3}&2&{ – 1}\\ 2&{ – 4}&3 \end{array}} \right]\) then,

\({C_{11}} = {( – 1)^{1 + 1}}{M_{11}} = {M_{11}} = \left| {\begin{array}{*{20}{c}} 2&{ – 1}\\ { – 4}&3 \end{array}} \right| = 2\)

\({C_{12}} = {( – 1)^{1 + 2}}{M_{12}} = – Minor\,of\,{a_{12}} = – \left| {\begin{array}{*{20}{c}} { – 3}&{ – 1}\\ 2&3 \end{array}} \right| = – ( – 9 + 2) = 7\)

\({C_{13}} = {( – 1)^{1 + 3}}{M_{13}} = Minor\,of\,{a_{13}} = \left| {\begin{array}{*{20}{c}} { – 3}&2\\ 2&{ – 4} \end{array}} \right| = 12 – 4 = 8\)

\({C_{21}} = {( – 1)^{2 + 1}}{M_{21}} = – Minor\,of\,{a_{21}} = – \left| {\begin{array}{*{20}{c}} 2&3\\ { – 4}&3 \end{array}} \right| = – (6 + 12) = – 18\)

\({C_{22}} = {( – 1)^{2 + 2}} = {M_{22}} = Minor\,of\,{a_{22}} = \left| {\begin{array}{*{20}{l}} 1&3\\ 2&3 \end{array}} \right| = 3 – 6 = – 3\)

\({C_{23}} = {( – 1)^{2 + 3}}{M_{23}} = – Minor\,of\,{a_{23}} = – \left| {\begin{array}{*{20}{c}} 1&2\\ 2&{ – 4} \end{array}} \right| = 4 + 4 = 8\)

\({C_{31}} = {( – 1)^{3 + 1}}{M_{31}} = Minor\,of\,{a_{31}} = \left| {\begin{array}{*{20}{c}} 2&3\\ 2&{ – 1} \end{array}} \right| = – 2 – 6 = – 10\)

\({C_{32}} = – {M_{32}} = – Minor\,of\,{a_{32}} = – \left| {\begin{array}{*{20}{c}} 1&3\\ { – 3}&{ – 1} \end{array}} \right| = – ( – 1 + 9) = – 8\)

\({C_{33}} = {( – 1)^{3 + 3}} M_{33} = Minor\,of\,{a_{33}} = \left| {\begin{array}{*{20}{c}} 1&2\\ { – 3}&2 \end{array}} \right| = 2 + 6 = 8\)

Laplace Expansion Formula:

If \(A = \left[ {{a_{ij}}} \right]\) is an \(n-\)dimensional square matrix. Then, the sum of the product of any row’s (or column’s) elements with their corresponding cofactors is always equal to \(|A|\) or, \(\det \left( A \right).\)

i.e., \(|A| = \sum\limits_{i = 1}^n {{a_{ij}}} {C_{ij}}\) and \(|A| = \sum\limits_{j = 1}^n {{a_{ij}}} {C_{ij}}\)

This formula is known as the Laplace Expansion Formula.

It allows us to express the determinant of a matrix as a linear combination of determinants of smaller matrices, called minors.

Verification:

Let \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]\) be a square matrix of order \( 3.\) Then, by definition, we have

\(|A| = \left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right|\)

Expanding along the first row, we have

\( \Rightarrow |A| = {( – 1)^{1 + 1}}{a_{11}}\left| {\begin{array}{*{20}{l}} {{a_{22}}}&{{a_{23}}}\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{1 + 2}}{a_{12}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {( – 1)^{1 + 3}}{a_{13}}\left| {\begin{array}{*{20}{l}} {{a_{21}}}&{{a_{22}}}\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right|\)

By using the definition of cofactors, we have

\(|A| = {a_{11}}{C_{11}} + {a_{12}}{C_{12}} + {a_{13}}{C_{13}}\)

Similarly, we have

\(|A| = {a_{21}}{C_{21}} + {a_{22}}{C_{22}} + {a_{23}}{C_{23}}\), \(|A| = {a_{31}}{C_{31}} + {a_{32}}{C_{32}} + {a_{33}}{C_{33}}\),
\(|A| = {a_{11}}{C_{11}} + {a_{21}}{C_{21}} + {a_{31}}{C_{31}}\) etc.

Note: If \(A = \left[ {{a_{ij}}} \right]\) is an \(n−\)dimensional square matrix. Then, when elements of any row (or column) in \(A\) are multiplied by cofactors from any other row (or column). Then their sum is equal to zero.

i.e., \(\sum\limits_{j = 1}^n {{a_{ij}}} {C_{kj}} = 0\) and, \(\sum\limits_{i = 1}^n {{a_{ij}}} {C_{ik}} = 0.\)

Example: Let \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]\) be a square matrix of order \(3.\)

Then, the sum of the product of elements of first row with the cofactors of elements in second row is given by

\({a_{11}}{C_{21}} + {a_{12}}{C_{22}} + {a_{13}}{C_{23}}\)

\( = {a_{11}}{( – 1)^{2 + 1}}\left| {\begin{array}{*{20}{l}} {{a_{12}}}&{{a_{13}}}\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right| + {a_{12}}{( – 1)^{2 + 2}}\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{13}}}\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right| + {a_{13}}{( – 1)^{2 + 3}}\left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right|\)

\( = – {a_{11}}\left( {{a_{12}} \cdot {a_{33}} – {a_{13}}{a_{32}}} \right) + {a_{12}}\left( {{a_{11}}{a_{33}} – {a_{13}}{a_{31}}} \right) – {a_{13}}\left( {{a_{11}}{a_{32}} – {a_{12}}{a_{31}}} \right)\)

\( = – {a_{11}}{a_{12}}{a_{33}} + {a_{11}}{a_{13}}{a_{32}} + {a_{12}}{a_{11}}{a_{33}} – {a_{12}}{a_{13}}{a_{31}} – {a_{13}}{a_{11}}{a_{32}} + {a_{13}}{a_{12}}{a_{31}}\)

\(=0\)

Determinant of a Fourth or Higher Order Square Matrix

To evaluate the determinant of a square matrix of order \(4\) or more we follow the same procedure as discussed in evaluating the determinant of a square matrix of order \(3.\)

Example, \(\Delta = \left| {\begin{array}{*{20}{c}} 1&2&{ – 1}&3\\ 2&1&{ – 2}&3\\ 3&1&2&1\\ 1&{ – 1}&0&2 \end{array}} \right|\)

Expanding the determinant along the first row, we have

\(\Delta = {( – 1)^{1 + 1}}(1)\left| {\begin{array}{*{20}{c}} 1&{ – 2}&3\\ 1&2&1\\ { – 1}&0&2 \end{array}} \right| + {( – 1)^{1 + 2}}(2)\left| {\begin{array}{*{20}{c}} 2&{ – 2}&3\\ 3&2&1\\ 1&0&2 \end{array}} \right| + {( – 1)^{1 + 3}}( – 1)\left| {\begin{array}{*{20}{c}} 2&1&3\\ 3&1&1\\ 1&{ – 1}&2 \end{array}} \right|\)
\(+ {( – 1)^{1 + 4}}(3)\left| {\begin{array}{*{20}{c}} 2&1&{ – 2}\\ 3&1&2\\ 1&{ – 1}&0 \end{array}} \right|\)

\( = 1(4 – 0) + 2(2 + 1) + 3(0 + 2) – 2[2(4 – 0) + 2(6 – 1) + 3(0 – 2)]\)
\( – 1(2(2 + 1) – 1(6 – 1) + 3( – 3 – 1)] – 3[2(0 + 2) – 1(0 – 2) – 2( – 3 – 1)]\)

\( = 4 + 6 + 6 – 2[8 + 10 – 6] – [6 – 5 – 12] – 3[4 + 2 + 8]\)

\( = 1(16) – 2(12) + ( – 1)( – 11) – 3(14)\)

\(\therefore \Delta = – 39\)

Remark:

It is evident from the above discussion that every square matrix \(A = \left[ {{a_{ij}}} \right]\) of order \(n\) can be associated with a number (real or imaginary) or an expression which is called the determinant of the square matrix \(A.\) Thus, determinant may be thought as a function of the set of all square matrices \(M,\) to the set of all numbers (real or imaginary).

Solved Examples – Determinants

Q.1. Evaluate \(\Delta = \left| {\begin{array}{*{20}{c}} 2&3&{ – 2}\\ 1&2&3\\ { – 2}&1&{ – 3} \end{array}} \right|\) by expanding it along the second row.
Ans: Given,\(\Delta = \left| {\begin{array}{*{20}{c}} 2&3&{ – 2}\\ 1&2&3\\ { – 2}&1&{ – 3} \end{array}} \right|\)
Expanding it along the second row, we have,
\(\Delta = {( – 1)^{2 + 1}}(1)\left| {\begin{array}{*{20}{l}} 3&{ – 2}\\ 1&{ – 3} \end{array}} \right| + {( – 1)^{2 + 2}}(2)\left| {\begin{array}{*{20}{c}} 2&{ – 2}\\ { – 2}&{ – 3} \end{array}} \right| + {( – 1)^{2 + 3}}(3)\left| {\begin{array}{*{20}{c}} 2&3\\ { – 2}&1 \end{array}} \right|\)
\( = – \left| {\begin{array}{*{20}{l}} 3&{ – 2}\\ 1&{ – 3} \end{array}} \right| + 2\left| {\begin{array}{*{20}{c}} 2&{ – 2}\\ { – 2}&{ – 3} \end{array}} \right| – 3\left| {\begin{array}{*{20}{c}} 2&3\\ { – 2}&1 \end{array}} \right|\)
\( = – ( – 9 + 2) + 2( – 6 – 4) – 3(2 + 6)\)
\( = 7 – 20 – 24\)
\(\therefore \Delta = – 37\)

Q.2. Find the minors and cofactors of elements of the matrix \( A = [{a_{ij}}] = \left[ {\begin{array}{*{20}{c}} 1&3&{ – 2}\\ 4&{ – 5}&6\\ 3&5&2 \end{array}} \right].\)
Ans: Given,
\(\left[ {\begin{array}{*{20}{c}} 1&3&{ – 2}\\ 4&{ – 5}&6\\ 3&5&2 \end{array}} \right].\)
Let \({M_{ij}}\) and \({C_{ij}}\) denote respectively the minor and cofactor of element aij in \(A.\) Then,
\({M_{11}} = \left| {\begin{array}{*{20}{c}} { – 5}&6\\ 5&2 \end{array}} \right| = – 10 – 30 = – 40 \Rightarrow {{\rm{C}}_{11}} = {M_{11}} = – 40\)
\({M_{12}} = \left| {\begin{array}{*{20}{l}} 4&6\\ 3&2 \end{array}} \right| = 8 – 18 = – 10 \Rightarrow {{\rm{C}}_{12}} = – {{\rm{M}}_{12}} = 10\)
\({M_{13}} = \left| {\begin{array}{*{20}{c}} 4&{ – 5}\\ 3&5 \end{array}} \right| = 20 + 15 = 35 \Rightarrow {C_{13}} = {M_{13}} = 35\)
\({M_{21}} = \left| {\begin{array}{*{20}{c}} 3&{ – 2}\\ 5&2 \end{array}} \right| = 6 + 10 = 16 \Rightarrow {C_{21}} = – {M_{21}} = – 16\)
\({M_{22}} = \left| {\begin{array}{*{20}{c}} 1&{ – 2}\\ 3&2 \end{array}} \right| = 2 + 6 = 8 \Rightarrow {C_{22}} = {M_{22}} = 8\)
\({M_{23}} = \left| {\begin{array}{*{20}{l}} 1&3\\ 3&5 \end{array}} \right| = 5 – 9 = – 4 \Rightarrow {C_{23}} = – {M_{23}} = 4\)
\({M_{31}} = \left| {\begin{array}{*{20}{c}} 3&{ – 2}\\ { – 5}&6 \end{array}} \right| = 18 – 10 = 8 \Rightarrow {C_{31}} = {M_{31}} = 8\)
\({M_{32}} = \left| {\begin{array}{*{20}{c}} 1&{ – 2}\\ 4&6 \end{array}} \right| = 6 + 8 = 14 \Rightarrow {C_{32}} = – {M_{32}} = – 14\)
\({M_{33}} = \left| {\begin{array}{*{20}{c}} 1&3\\ 4&{ – 5} \end{array}} \right| = – 5 – 12 = – 17 \Rightarrow {C_{33}} = {M_{33}} = – 17\)

Q.3. If \(\left[ {\,} \right]\) denotes the greatest integer less than or equal to the real number under consideration, and \( – 1 \leqslant x < 0,0 \leqslant y < 1,1 \leqslant z < 2\) then find the value of the following determinant:
\(\Delta = \left| {\begin{array}{*{20}{c}} {[x] + 1}&{[y]}&{[z]}\\ {[x]}&{[y] + 1}&{[z]}\\ {[x]}&{[y]}&{[z] + 1} \end{array}} \right|\)
Ans: We have \( – 1 \leqslant x < 0,0 \leqslant y < 1,1 \leqslant z < 2\)
\( \Rightarrow [x] = – 1,[y] = 0\) and \([z] = 1.\)
\(\therefore \Delta = \left| {\begin{array}{*{20}{c}} {[x] + 1}&{[y]}&{[z]}\\ {[x]}&{[y] + 1}&{[z]}\\ {[x]}&{[y]}&{[z] + 1} \end{array}} \right|\)
\( \Rightarrow \Delta = \left| {\begin{array}{*{20}{c}} 0&0&1\\ { – 1}&1&1\\ { – 1}&0&2 \end{array}} \right|\)
\( = 0 \times \left| {\begin{array}{*{20}{l}} 1&1\\ 0&2 \end{array}} \right| – 0 \times \left| {\begin{array}{*{20}{l}} { – 1}&1\\ { – 1}&2 \end{array}} \right| + 1 \times \left| {\begin{array}{*{20}{l}} { – 1}&1\\ { – 1}&0 \end{array}} \right|\)
\( = 0(2 – 0) – 0( – 2 + 1) + 1 \times (0 + 1)\)
\(\therefore \Delta = 1\)

Q.4. Evaluate the determinant \(\Delta = \left| {\begin{array}{*{20}{c}} 1&{\sin \theta }&1\\ { – \sin \theta }&1&{\sin \theta }\\ { – 1}&{ – \sin \theta }&1 \end{array}} \right|.\) Also, prove that \(2 \leqslant \Delta \leqslant 4\).
Ans: Given: \(\Delta = \left| {\begin{array}{*{20}{c}} 1&{\sin \theta }&1\\ { – \sin \theta }&1&{\sin \theta }\\ { – 1}&{ – \sin \theta }&1 \end{array}} \right|\)
Expanding along the first row, we have,
\(\Delta = 1 \times \left| {\begin{array}{*{20}{c}} 1&{\sin \theta }\\ { – \sin \theta }&1 \end{array}} \right| – \sin \theta \left| {\begin{array}{*{20}{c}} { – \sin \theta }&{\sin \theta }\\ { – 1}&1 \end{array}} \right| + 1 \times \left| {\begin{array}{*{20}{c}} { – \sin \theta }&1\\ { – 1}&{ – \sin \theta } \end{array}} \right|\)
\( = 1 \times \left( {1 + {{\sin }^2}\theta } \right) – \sin \theta ( – \sin \theta + \sin \theta ) + 1 \times \left( {{{\sin }^2}\theta + 1} \right)\)
\( = 2\left( {1 + {{\sin }^2}\theta } \right)\)
\(\because \; – 1 \leqslant \sin \theta \leqslant 1\) for all \(\theta \).
\( \Rightarrow 0 \leqslant {\sin ^2}\theta \leqslant 1\) for all \(\theta \).
\( \Rightarrow 1 + 0 \leqslant 1 + {\sin ^2}\theta \leqslant 1 + 1\) for all \(\theta \).
\( \Rightarrow 1 \leqslant 1 + {\sin ^2}\theta \leqslant 2\) for all \(\theta \).
\( \Rightarrow 2 \leqslant 2\left( {1 + {{\sin }^2}\theta } \right) \leqslant 4\) for all \(\theta \)
\( \Rightarrow 2 \leqslant \Delta \leqslant 4\) for all \(\theta \).

Q.5. Evaluate the determinant of the following matrix using the Laplace expansion by the second row:
\(A = \left[ {\begin{array}{*{20}{c}} 2&{ – 1}&{ – 1}\\ { – 3}&2&1\\ 5&0&{ – 2} \end{array}} \right]\)
Ans: Given: \(A = \left[ {\begin{array}{*{20}{c}} 2&{ – 1}&{ – 1}\\ { – 3}&2&1\\ 5&0&{ – 2} \end{array}} \right]\)
Let \({C_{ij}}\) denote the cofactor of element \({a_{ij}}\) in \(A.\)
Using the Laplace Expansion formula, and expanding the determinant along the second row, we have
\(|A| = {a_{21}}{C_{21}} + {a_{22}}{C_{22}} + {a_{23}}{C_{23}}\)
\( = – 3 \times {( – 1)^{2 + 1}}\left| {\begin{array}{*{20}{c}} { – 1}&{ – 1}\\ 0&{ – 2} \end{array}} \right| + (2){( – 1)^{2 + 2}}\left| {\begin{array}{*{20}{c}} 2&{ – 1}\\ 5&{ – 2} \end{array}} \right| + (1){( – 1)^{2 + 3}}\left| {\begin{array}{*{20}{c}} 2&{ – 1}\\ 5&0 \end{array}} \right|\)
\( = 3(2 – 0) + 2( – 4 + 5) – (0 + 5)\)
\( = 6 + 2 – 5\)
\(=3\)

Summary

This article explains about the method of finding the determinant of a matrix of order \(n..\) The minor \({M_{ij}}\) of \({a_{ij}}\) in \(A\) is the determinant of the square sub-matrix of order \(\left( {n – 1} \right)\) obtained by leaving \({i^{{\text{th}}}}\) row and \({j^{{\text{th}}}}\) column of \(A.\) The cofactor \({C_{ij}}\) of \({a_{ij}}\) in \(A\) is equal to \({( – 1)^{i + j}}\) times the determinant of the sub-matrix of order \(\left( {n – 1} \right)\) obtained by leaving \({i^{{\text{th}}}}\) row and \({j^{{\text{th}}}}\) column of \(A.\) We have also verified that the sum of the product of elements of any row (column) with their cofactors is always equal to \(\left| A \right|\) or, \(\det \left( A \right)\) which is also known as the Laplace Expansion Formula.

Frequently Asked Questions (FAQs)

Q.1. What are determinants with examples?
Ans: Every square matrix \(A = \left[ {{a_{ij}}} \right]\) of order \(n\) can be associated to a number (real or complex) or an expression which is called determinant of the square matrix \(A.\)
Example: Let \(A = \left[ {\begin{array}{*{20}{l}} 1&2&3\\ 4&5&6\\ 7&8&0 \end{array}} \right]\) then determinant of \(A\) is denoted by \(\det A,\) or \(|A|,\) or \(\left| {\begin{array}{*{20}{l}} 1&2&3\\ 4&5&6\\ 7&8&0 \end{array}} \right|,\) and its value is evaluated as follows:
\(|A| = 1(0 – 48) – 2(0 – 42) + 3(32 – 35)\)
\( = – 48 + 84 – 9\)
\( = 27\)
Hence, the determinant of \(A = 27.\)

Q.2. What are determinants used for?
Ans: Determinants can be used to provide explicit formulae for solving a system of \(n\) equations in \(n\) unknowns, as well as for finding the inverse of an invertible matrix. They may also be used to calculate the area or volume of geometric figures.

Q.3. What are the different types of determinants?
Ans: There are commonly three types of determinants:
First Order Determinant: If \(A = \left[ {{a_{11}}} \right]\) is a square matrix of order \(1,\) then the determinant of \(A\) is written as \(|A| = {a_{11}},\) or \(\left| {{a_{11}}} \right| = {a_{11}}.\)
Second-Order Determinant: The second-order determinant is the determinant of a matrix of order \(2.\) It is evaluated as follows:
Let \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right]\) then \(|A| = \left| {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right| = {a_{11}}{a_{22}} – {a_{21}}{a_{12}}.\)
Third-Order Determinant: The third-order determinant is used to find the determinant of a matrix of order \(3.\)
Let \(A = \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]\) then \(|A| = {a_{11}}\left( {{a_{22}}{a_{33}} – {a_{23}}{a_{32}}} \right) – {a_{12}}\left( {{a_{21}}{a_{33}} – {a_{23}}{a_{31}}} \right) + {a_{13}}\left( {{a_{21}}{a_{32}} – {a_{22}}{a_{31}}} \right)\).

Q.4. What are the 4 determinants of demand?
Ans: The four determinants of demand are:
1. The price of the good or service
2. The income of buyers
3. Consumer tastes or preferences will drive demand.
4. Consumer predictions regarding whether product prices will grow or decline in the future

Q.5. What is the concept of determinant?
Ans: Determinants are scalar quantities calculated by adding the sums of the products of the elements of a square matrix according to a set of rules.

Learn about Singular Matrix here

Hope this detailed article on Determinants helps you in your preparation. In case of any query, reach out to us in the comment section and we will get back to you at the earliest.