Distance Formula and Its Application: 2D Plane, 3D Plane, Parallel Lines in 2D

Distance Formula and its Application: As the name implies, the distance formula calculates the distance between two points (the length of the line segment). The length of the line segment connecting two places, for example, is the distance between them. The Pythagoras theorem is used to obtain the distance formula between two points in a two-dimensional plane, which may also be extended to find the distance between two points in a three-dimensional plane. In coordinate geometry, there are several different forms of distance formulas. The distance formula is an algebraic statement that calculates the distance between two places in terms of their coordinates.

Distance between Two Points in a 2D Plane

The length of the path between two places or points is the distance between these two places or points. This distance is determined by using a scale or a measuring tape to find the distance. When coordinates of two points are known, it is impossible to measure the distance with a scale or a measuring tape, and we use the distance formula to find the distance.

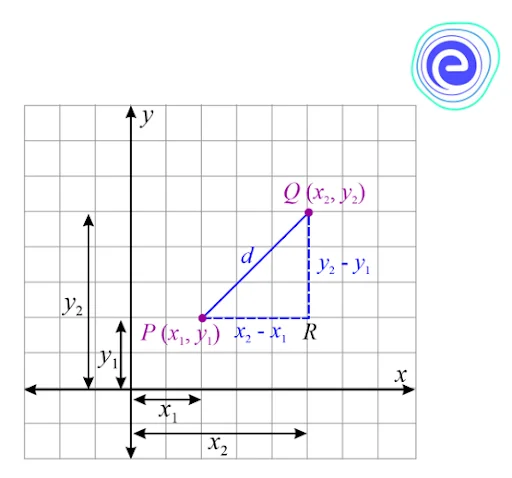
The Euclidean distance formula is a distance formula that is used to find the distance between two locations in a two-dimensional plane. Let us consider two locations in the \(2D\) plane, \(P\left(x_{1}, y_{1}\right)\) and \(\mathrm{Q}\left(x_{2}, y_{2}\right)\) to get the formula. Assume the distance between \(P\) and \(Q\) is \(d.\)

Study Everything About Distance Formula

Distance Formula Derivation

By the Pythagoras theorem,

\(P Q^{2}=P R^{2}+Q R^{2}\)

\(d^{2}=\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\)

On both sides, take the square root.

\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) units

\(d=\sqrt{(\text { Difference of abscissae })^{2}+(\text { Difference of ordinates })^{2}}\)

This is the formula to calculate the distance between two points.

Distance of a Point in Two Dimensions From the Origin

In particular, the distance of a point \(A(x,y)\) from the origin \(O(0,0)\) is given by \(O A=\sqrt{x^{2}+y^{2}}\) units.

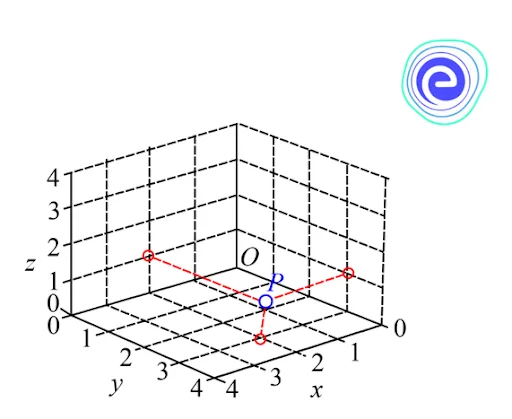
Distance between Two Points in a 3D Plane

In contrast to two-dimensional space, which has only one plane, the \(xy\)-plane, three-dimensional space has an endless number of planes, just as two-dimensional space has an infinite number of lines. The \(xy\)-plane, which contains the \(x\)-axes and \(y\)-axes; the \(yz\)-plane, which contains the \(y\)-axes and \(z\)-axes; and the \(xz\)-plane, which contains the \(x\)-axes and \(z\)-axes, are all significant.

The distance formula states that the distance between two points in \(xyz\)-space is the square root of the sum of the squares of the differences between corresponding coordinates. That is, given \(P\left(x_{1}, y_{1}, z_{1}\right)\) and \(Q\left(x_{2}, y_{2}, z_{2}\right)\) the distance between \(P\) and \(Q\) is given by 

\(P Q=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\) units

Similarly, the distance of a point \(P(x,y,z),\) in three dimensions from the origin \(O(0,0,0)\) can be given by

\(O P=\left(\sqrt{(0-x)^{2}+(0-y)^{2}+(0-z)^{2}}\right)=\sqrt{x^{2}+y^{2}+z^{2}}\)

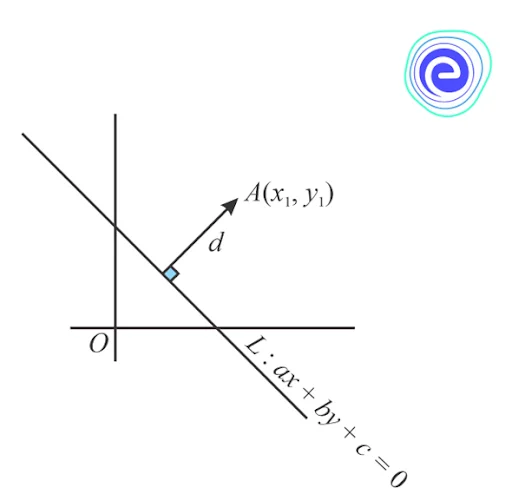
Distance from a Point to a Line in 2D

The length of the perpendicular line segment drawn from the line is the distance formula for calculating the distance between two points. Consider a line \(L\) in a two-dimensional plane with the equation \(ax+by+c=0\) and a point \(A\left(x_{1}, y_{1}\right)\) on it. The distance \((d)\) between \(P\) and \(L\) is then,

\(d = \frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) units

is the formula to find the distance from a point to a line in \(2D\).

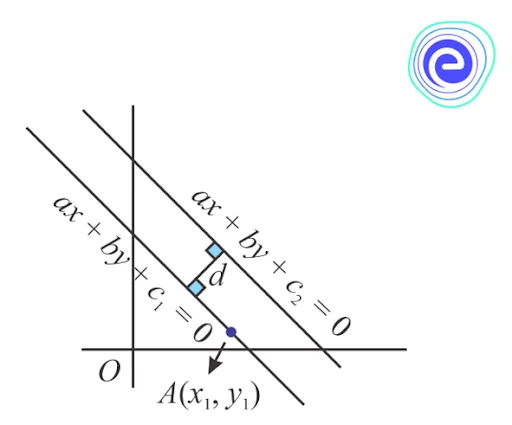
Distance between Two Parallel Lines in 2D

The slopes of two parallel lines are usually the same, as we know. As a result, we can conclude that the two parallel lines are \(a x+b y+c_{1}=0\) and \(a x+b y+c_{2}=0\). Then the distance \((d)\) between the two parallel lines is 

\(d=\frac{\left|c_{2}-c_{1}\right|}{\sqrt{a^{2}+b^{2}}}\) units

Distance from a Point to a Line in 3D

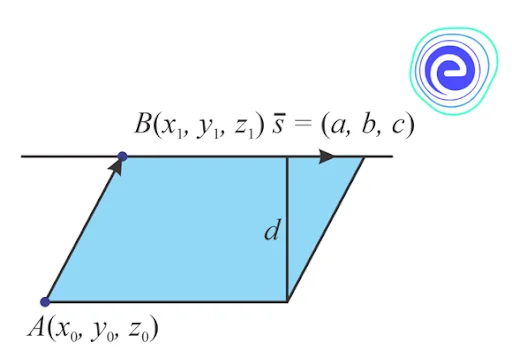
The distance formula to determine the distance from the point to a line in a \(3D\), consider a point \(A\left(x_{0}, y_{0}, z_{0}\right)\) and a line \(l\) with point \(B\) on it in \(3D\) whose equation is \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\) So the distance \((d)\) from the point \(A\) to the line \(l\) is,

\(d=\frac{|\overline{A B} \times \bar{s}|}{|\bar{s}|}\) units

Where \(A\) is the point from which calculating the distance to the line \(l\). The coordinates of the point \(A\) is \(\left(x_{0}, y_{0}, z_{0}\right)\)

\(B\) is the point on the line \(l\), and the coordinates of the point \(B\) is \(\left(x_{1}, y_{1}, z_{1}\right)\)

\(\overline{A B}=\left(x_{1}-x_{0}, y_{1}-y_{0}, z_{1}-z_{0}\right)\)

\(\bar{s}=\langle a, b, c\rangle\) is the direction vector of the line \(l\).

Applications of the Distance Formula

The distance formula comes with some uses in everyday life. It can be used as a strategy for easy navigation and distance estimation. For example, to estimate the distance of two places on a map, simply get the coordinate of the two places and apply the formula.

Solved Examples on Distance Formula and its Application

Q.1. Find the distance between the coordinates \(P\left( {2,\,3} \right)\) and \(Q\left( { – 4,\,5} \right).\)
Ans: Given, the coordinates \(P(2,3)\) and \(Q(-4,5)\)
Here, \(x_{1}=2, y_{1}=3, x_{2}=-4\) and \(y_{2}=5\)
We know that Distance \(=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Now, \(P Q=\sqrt{(-4-2)^{2}+(5-3)^{2}}=\sqrt{36+4}=\sqrt{40}\) units
Hence, the distance between two given coordinates is \(\sqrt{40}\) units.

Q.2. Find the distance between the coordinate \(A\left( { – 2,\, – 3} \right)\) and the origin.
Ans: Given, the coordinate \(A(-2,-3)\) and the origin \(O(0,0)\).
Here, \(x_{1}=-2, y_{1}=-3, x_{2}=0\) and \(y_{2}=0\)
We know that Distance \(=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Now, \(A B=\sqrt{(0-(-2))^{2}+(0-(-3))^{2}}=\sqrt{2^{2}+3^{2}}=\sqrt{4+9}=\sqrt{13}\) units
Hence, the distance between the given coordinate and origin is \(\sqrt{13}\) units.

Q.3. Find a relation between \(x\) and \(y\) such that the point \(A\left( {x,\,y} \right)\) is equidistant from the points \(B\left( {2,\,1} \right)\) and \(C\left( {1,\,3} \right).\)
Ans: Given, the coordinates \(B(2,1)\) and \(C(1,3)\) are equidistance from the point \(A(x,y)\).
That is, \(AB=BC\)
We know that Distance \(=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(A B=\sqrt{(2-x)^{2}+(1-y)^{2}}\) and \(B C=\sqrt{(1-x)^{2}+(3-y)^{2}}\)
Now, \(\sqrt{(2-x)^{2}+(1-y)^{2}}\)
\(=\sqrt{(1-x)^{2}+(3-y)^{2}}\)
By squaring on both sides, we get
\(\Rightarrow 4+x^{2}-4 x+1+y^{2}-2 y=1+x^{2}-2 x+9+y^{2}-6 y\)
\(\Rightarrow 5-4 x-2 y\)
\(=10-2 x-6 y\)
\(\Rightarrow 2 x-4 y-5=0\)
Hence, the relation between \(x\) and \(y\) is \(2x-4y-5=0.\)

Q.4. Calculate the distance between \(A\left( {3,\, – 5} \right)\) and the line \(3x – 4y = 5.\)
Ans: Given \(A(3,-5)\) and the equation of the line \(3x-4y=5\)
By comparing the equation of line \(3x-4y=5\) with the standard form of the equation \(ax+by+c=0\), we get \(a=3, b=-4\) and \(c=-5.\)
The distance formula to determine the distance from the point to a line is \(d=\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
\(d=\frac{|3(3)-4(-5)-5|}{\sqrt{3^{2}+(-4)^{2}}}=\frac{24}{5}\) units 
Hence, the distance between the point \(A\) and the given line is \(\frac{24}{5}\) units.

Q.5. Determine the distance from the point \(\left( { – 1,\,2,\,5} \right)\) to the line \(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-3}{3}\)
Ans: Given, \((-1,2,5)=A\left(x_{0}, y_{0}, z_{0}\right)\)
By comparing the line \(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-3}{3}\) with \(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\), we get
\(B\left(x_{1}, y_{1}, z_{1}\right)=(2,-1,3)\)
\(\bar{s}=<1,2,3>\)
Now, \(\overline{A B}=\left(x_{1}-x_{0}, y_{1}-y_{0}, z_{1}-z_{0}\right)=(2+1,-1-2,3-5)=(3,-3,-2)\)
Now, we must find the cross product of \(\overline{A B} \times \bar{s}\)
That is, \(\overline {AB} \times \overline s = \left| {\begin{array}{*{20}{c}} i&j&k\\ 3&{ – 3}&{ – 2}\\ 1&2&3 \end{array}} \right|\)
\(=(-9+4),(9+2),(6+3)\)
\(=<-5,11,9>\) 
\(|\overline{A B} \times \bar{s}|=\sqrt{(-5)^{2}+11^{2}+9^{2}}=\sqrt{227}\) and \(\bar{s}=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{14}\)
Using the formula \(d=\frac{|\overline{A B} \times \bar{s}|}{|\vec{s}|}\) units, we get
\(=\frac{\sqrt{227}}{\sqrt{14}}=\frac{15.066}{3.741}=4.027\)
Hence, the distance from the point \((-1,2,5)\) to the given line is \(4.027.\)

Summary

The length of the path between two places or points is the distance between these two places or points. In this article, we learned about the distance between two points in a \(2D\) plane, the distance between two points in a \(3D\) plane, distance from a point to a line in \(2D,\) the distance between two parallel lines in \(2D,\) distance from a point to a line in \(3D,\) applications of distance formula, solved examples on distance formula and its application, FAQs on distance formula and its application.

The learning outcome of this article is to estimate the distance of two places on a map, get the coordinate of the two places and apply the formula.

FAQs on Distance Formula and its Application

Q.1. What is the distance formula?
Ans: As the name says, any distance formula estimates the distance between two places (the length of the line segment). The distance between two points, for example, is the length of the line segment joining them. The Pythagoras theorem is used to calculate the distance between two points in a two-dimensional plane. It can also be used to calculate the distance between two points on a three-dimensional plane. Distance formulas come in several different forms in coordinate geometry. The distance formula is an algebraic expression that estimates the distance between two points using their coordinates.

Q.2. What is the distance formula in coordinate geometry?
Ans: The Euclidean distance formula is a distance formula that is used to find the distance between two locations in a two-dimensional plane. Let us consider two locations in the \(2D\) plane, \(P\left(x_{1}, y_{1}\right)\) and \(\mathrm{Q}\left(x_{2}, y_{2}\right)\) to get the formula. Assume the distance between \(P\) and \(Q\) is \(d\).
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) units

Q.3. What are the applications of the distance formula?
Ans: The distance formula comes with some uses in everyday life. It can be used as a strategy for easy navigation and distance estimation. For example, to estimate the distance of two places on a map, simply get the coordinate of the two places and apply the formula.

Q.4. What is the 3D distance formula?
Ans: The distance formula states that the distance between two points in \(xyz\)-space is the square root of the sum of the squares of the differences between corresponding coordinates. That is, given \(P\left(x_{1}, y_{1}, z_{1}\right)\) and \(Q\left(x_{2}, y_{2}, z_{2}\right)\) the distance between \(P\) and \(Q\) is given by \(P Q=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\) units.

Q.5. What is the distance formula and example?
Ans: In coordinate geometry, the distance formula is used to calculate the distance between two points. The formula for calculating the distance between two points \(({x_1},{y_1}),({x_1},{y_1})\) and \(({x_2},{y_2}),({x_2},{y_2})\) is as follows:
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) units
Example: Find the distance between the coordinates \(A(1,5)\) and \(B(-2,3)\).
Solution: Given, the coordinates \(A(1,5)\) and \(B(-2,3)\)
Here, \(x_{1}=1, y_{1}=5, x_{2}=-2\) and \(y_{2}=3\)
We know that Distance \(=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Now, \(A B=\sqrt{(-2-1)^{2}+(3-5)^{2}}=\sqrt{9+4}=\sqrt{13}\) units
Hence, the distance between two given coordinates is \(13\) units.

Q.6. What is the distance between 2 points?
Ans: The length of the straight line connecting two locations in the coordinate plane is used to calculate the distance between them. Since this distance can never be negative, we use the absolute value when calculating the distance between two places.

Study Distance Formula in 3D Here

We hope this article on the distance formula and its application is helpful to you. If you have any queries related to this post, ping us through the comment box below and we will get back to you as soon as possible.