Distance of a Point from a Line: According to Euclidean geometry, distance from a point to a line is the shortest distance between a given point and a point on a line. The length of the line segment linking the given point to the (nearest point on the) line which is the point’s perpendicular distance to the line is the shortest distance between the point and the line The formula for measuring the distance between two points can be deduced and stated in different ways. Knowing the distance between the point and a line can be beneficial in a variety of real-life circumstances, such as determining the distance between two trees.

In this article, we will study how to calculate the distance of a point from a line in \(2d\) and \(3d\) using derivation and solved examples.

Derivation of the Distance of a Point from a Line:

The length of the perpendicular from a point \(\left( {{x_1},{y_1}} \right)\) to a line \(ax + by + c = 0\) is given by
\(\left| {\frac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|\)
Consider the line \(ax + by + c = 0\)
At \(y = 0,\) we have \(x = – \frac{c}{a}\)
At \(x = 0,\) we have \(y = – \frac{c}{b}\)
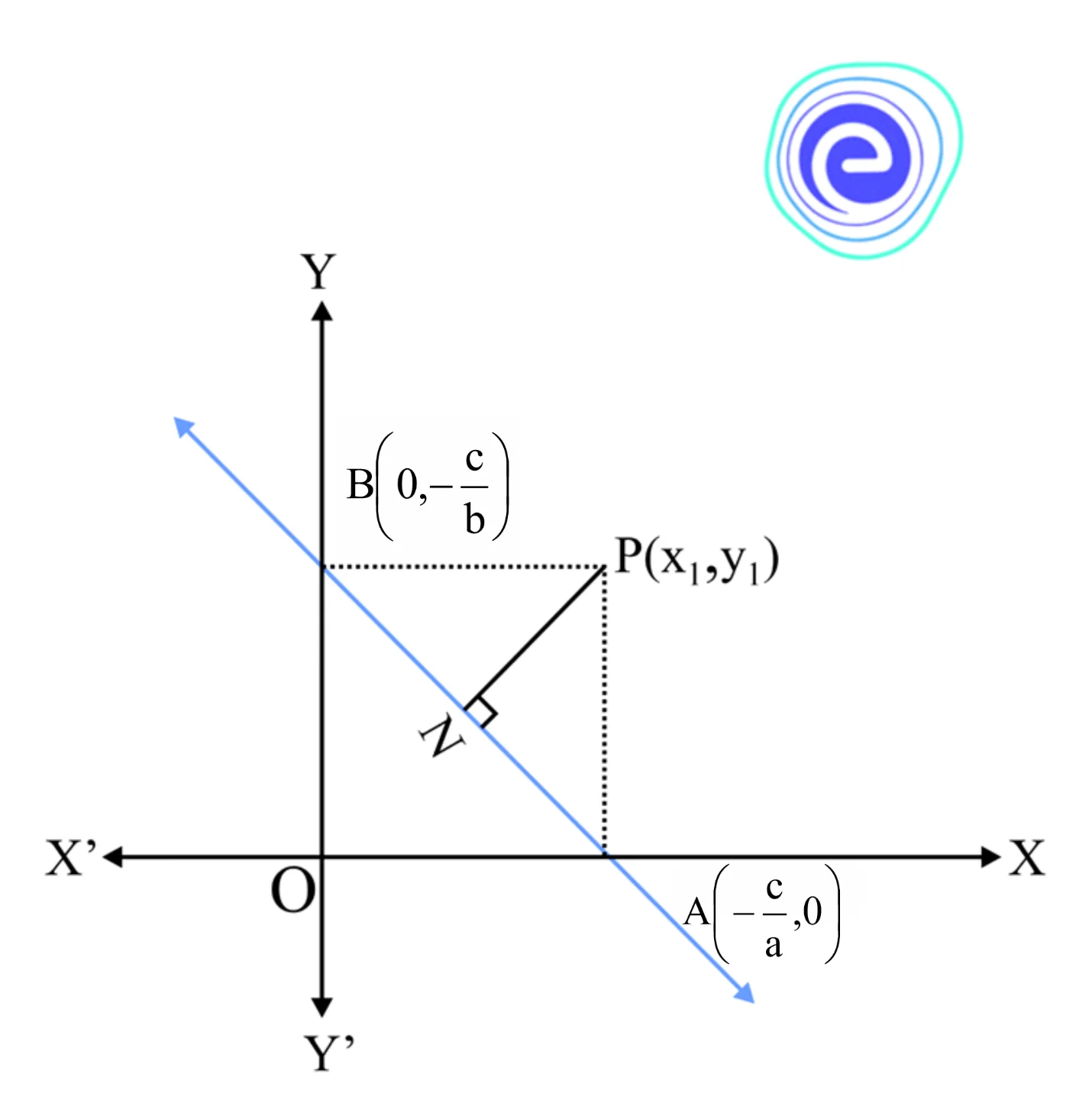
The graph of the line is as shown below:

Learn about Coordinates here

Let \(p\left( {{x_1},{y_1}} \right)\) be a point. Draw \(PN\) perpendicular to \(AB.\)
We know that the area of the triangle with vertices \(\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)\) is given by
\(A = \frac{1}{2}\left[ {{x_1}\left( {{y_2} – {y_3}} \right) + {x_2}\left( {{y_3} – {y_1}} \right) + {x_3}\left( {{y_1} – {y_2}} \right)} \right]\)
\(\therefore \) Area of triangle \(PAB = \frac{1}{2}\left| {{x_1}\left( {0 + \frac{c}{b}} \right) – \frac{c}{a}\left( { – \frac{c}{b} – {y_1}} \right) + 0\left( {{y_1} – 0} \right)} \right|\)
\( = \frac{1}{2}\left| {\frac{{c{x_1}}}{b} + \frac{{c{y_1}}}{a} + \frac{{{c^2}}}{{ab}}} \right|\)
\( = \left| {\left( {a{x_1} + b{y_1} + c} \right)\frac{{{c^2}}}{{2ab}}} \right|….\left( i \right)\)
Area of \(\Delta PAB = \frac{1}{2} \times AB \times PN\)
\( = \frac{1}{2}\sqrt {\frac{{{c^2}}}{{{a^2}}} + \frac{{{c^2}}}{{{b^2}}}} \times PN\) [Since the distance between two points \(A\left( {{x_1},{y_1}} \right)\) and \(B\left( {{x_2},{y_2}} \right)\) is \(\sqrt {{{\left( {{x_1} – {x_2}} \right)}^2} + {{\left( {{y_1} – {y_2}} \right)}^2}} \)]
\( = \frac{c}{{2ab}}\sqrt {{a^2} + {b^2}} \times PN…..\left( {ii} \right)\)
From \(\left( i \right)\) and \(\left( ii \right),\) we have,
\(\left| {\left( {a{x_1} + b{y_1} + c} \right)\frac{c}{{2ab}}} \right| = \frac{c}{{2ab}}\sqrt {{a^2} + {b^2}} \times PN\)
\( \Rightarrow PN = \frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) which is the required distance of a point \(\left( {{x_1},{y_1}} \right)\) from a line \(ax + by + c = 0.\)

Corollary:

The length of the perpendicular from the origin to the line \(ax + by + c = 0\) is \(\frac{{\left| c \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)

Algorithm for Finding the Length of the Perpendicular from a Point \(\left( {{x_1},{y_1}} \right)\) to the Line \(ax + by + c = 0:\)

1. Write the line’s equation in the form \(ax + by + c = 0.\)
2. In the expression, replace \(x\) and \(y\) with the coordinates \({x_1}\) and \({y_1}\) of the point, respectively.
3. Divide the expression obtained in the \({2^{nd}}\) step by the square root of the sum of the squares of the coefficients of \(x\) and \(y.\)
4. Take the modulus of the expression obtained in the \({3^{rd}}\) step, which is the required perpendicular length from the point \(\left( {{x_1},{y_1}} \right)\) to the line \(ax + by + c = 0.\)

Solved Examples on Distance of a Point from a Line in \(2D:\)

Q.1. Find the distance between the point \(\left( {2,1} \right)\) and the line \(12x – 5y + 9 = 0.\)
Ans: We know that the distance of a point \(\left( {{x_1},{y_1}} \right)\) from a line \(ax + by + c = 0\) is given by
\(\frac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Here,
\(\left( {{x_1},{y_1}} \right) = \left( {2,1} \right)\)
line is \(12x – 5y + 9 = 0\)
\(\therefore \) Required distance \( = \frac{{\left| {12 \times 2 + \left( { – 5} \right) \times 1 + 9} \right|}}{{\sqrt {{{12}^2} + {{\left( { – 5} \right)}^2}} }}\)
\( = \frac{{\left| {24 – 5 + 9} \right|}}{{\sqrt {169} }}\)
\( = \frac{{28}}{{13}}{\text{units}}\)

Q.2. If length of the perpendicular from the origin to the line \(\frac{x}{a} + \frac{y}{b} = 1\) is \(p,\) then prove that \({a^4} + {b^4} = 0,\) if \({a^2},{p^2},{b^2}\) are in A.P.
Ans: The equation of the given line is \(\frac{x}{a} + \frac{y}{b} = 1\)
\( \Rightarrow bx + ay – ab = 0\)
Given: \(p = \)length of the perpendicular from the origin to the given line
\(\therefore p = \frac{{\left| {b\left( 0 \right) + a\left( 0 \right) – ab} \right|}}{{\sqrt {{b^2} + {a^2}} }}\)
\( = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}\)
\( = \frac{{ab}}{{\sqrt {{a^2} + {b^2}} }}\)
\( \Rightarrow {p^2} = \frac{{{a^2}{b^2}}}{{{a^2} + {b^2}}}\)
\( \Rightarrow \frac{1}{{{p^2}}} = \frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}\)
\( \Rightarrow \frac{1}{{{p^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}}….\left( i \right)\)
Now, assuming that \({a^2},{p^2},{b^2}\) are in AP, we have,
\(2{p^2} = {a^2} + {b^2}\)
Now,
\(\frac{1}{{{p^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}}\) [From \(\left( i \right)\)]
\( \Rightarrow {p^2}\left( {{a^2} + {b^2}} \right) = {a^2}{b^2}\)
\( \Rightarrow \left( {\frac{{{a^2} + {b^2}}}{2}} \right)\left( {{a^2} + {b^2}} \right) = {a^2}{b^2}\)
\( \Rightarrow {\left( {{a^2} + {b^2}} \right)^2} = 2{a^2}{b^2}\)
\( \Rightarrow {a^4} + {b^4} = 0\)
Hence, proved that \({a^2},{p^2},{b^2}\) are in AP.

Distance of a Point from a Line in \(3D:\)

The perpendicular distance of a point from a plane can be calculated in vector form and cartesian form.

Vector Form:

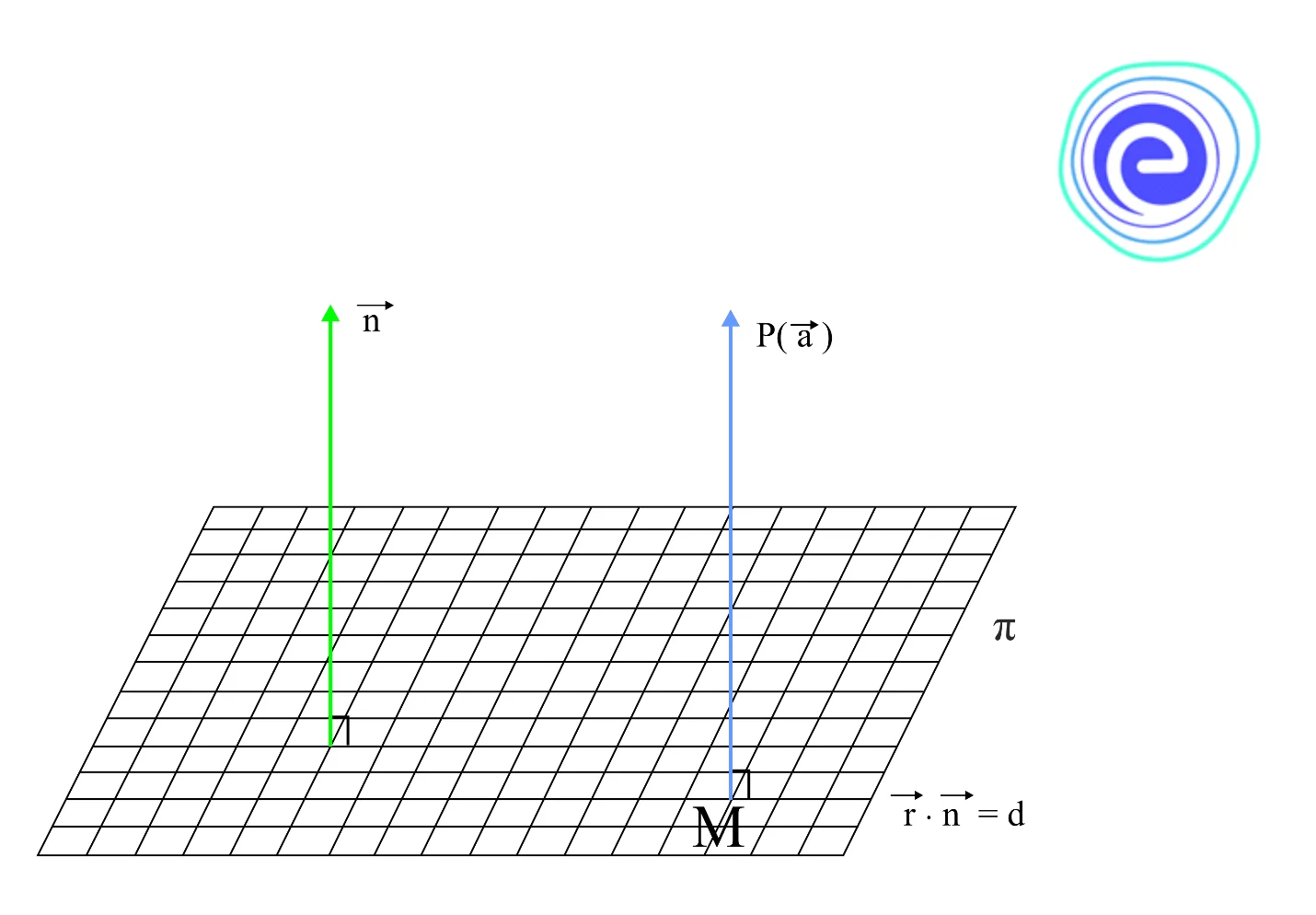
The length of the perpendicular from a point having position vector \(\mathop a\limits^ \to \) to the plane \(\vec r \cdot \vec n = d\) is \(p = \frac{{|\vec a \cdot \vec n – d|}}{{|\vec n|}}\)

Derivation:

Let \(\pi \) be the given plane, and \(P(\vec a)\) be the given point. Let \(PM\) be the length of the perpendicular from \(P\) on the plane . Since line PM passes through \(P(\vec a)\) and is parallel to the vector \(\vec n\) which is normal to the plane \(\pi .\) So, vector equation of line \(PM\) is
\(\vec r = \vec a + \lambda \vec n,\,\,\,…..(i)\)
where, \(\lambda \) is a scalar.
Clearly, point \(M\) is the intersection of line \((i)\) and the given plane. Therefore, point \(M\) must have,
\((\vec a + \lambda \vec n) \cdot \vec n = d\) [On substituting \(\vec r = \vec a + \lambda \vec n\) in the equation of the plane] \( \Rightarrow \vec a \cdot \vec n + \lambda \vec n \cdot \vec n = d\)
\( \Rightarrow \lambda = \frac{{d – (\vec a \cdot \vec n)}}{{\vec n \cdot \vec n}}\)
\( \Rightarrow \lambda = \frac{{d – (\vec a \cdot \vec n)}}{{|\vec n{|^2}}}\)
Substituting this value of \(\lambda \) in \((i)\), we obtain the position vector of \(M\) as
\(\vec r = \vec a + \left( {\frac{{d – (\vec a \cdot \vec n)}}{{|\vec n{|^2}}}} \right)\vec n\)
Now,
\(\overrightarrow {PM} = P.V.\) of \(M – P.V.\) of \(P\)
\( \Rightarrow \overrightarrow {PM} = \vec a + \left\{ {\frac{{d – (\vec a \cdot \vec n)}}{{|\vec n{|^2}}}} \right\}\vec n – \vec a\)
\( \Rightarrow \overrightarrow {PM} = \frac{{\{ d – (\vec a \cdot \vec n)\} \vec n}}{{|\vec n{|^2}}}\)
\(\therefore PM = |\overrightarrow {PM} | = \left| {\frac{{[d – (\vec a \cdot \vec n)]\vec n}}{{|\vec n{|^2}}}} \right|\)
\( \Rightarrow PM = \frac{{|\vec d – (\vec a \cdot \vec n)||\vec n|}}{{|\vec n{|^2}}}\)
\( \Rightarrow PM = \frac{{|(\vec a \cdot \vec n) – d|}}{{|\vec n|}}\)
Thus, the length of the perpendicular from a point having position vector \({\vec a}\) on the plane \(\vec r \cdot \vec n = d\) is given by \(\frac{{|(\vec a \cdot \vec n) – d|}}{{|\vec n|}}\)

Cartesian Form:

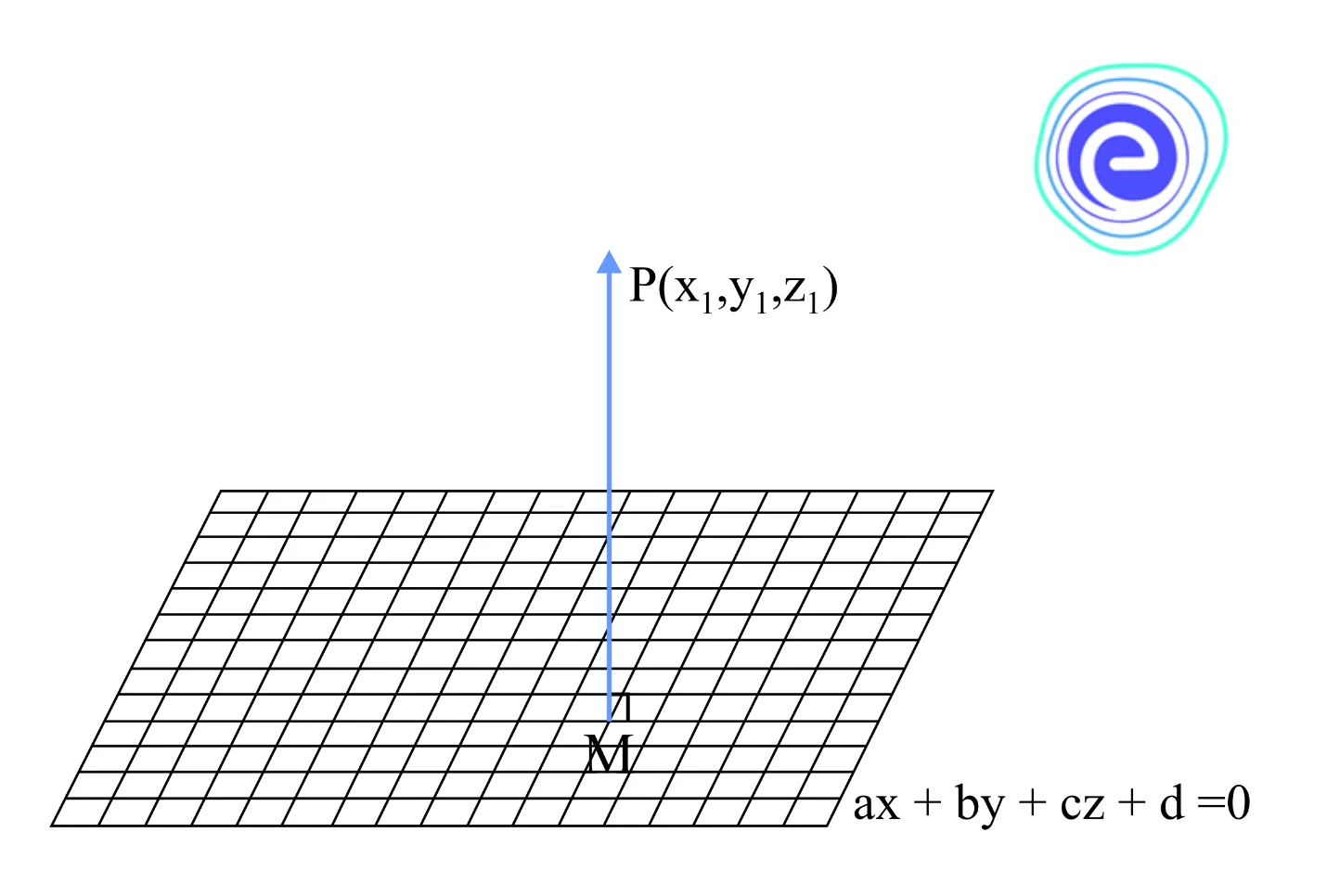
The length of the perpendicular from a point \(P\left( {{x_1},{y_1},{z_1}} \right)\) to the plane \(ax + by + cz + d = 0\) is given by \(p = \frac{{\left| {a{x_1} + b{y_1} + c{z_1} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}.\)
Let \(M\) be the foot of the perpendicular from \(P\left( {{x_1},{y_1},{z_1}} \right)\) to the plane \(ax + by + cz + d = 0.\)
Clearly, line \(PM\) passes through the point \(P\left( {{x_1},{y_1}} \right)\) and is normal to the plane. The equation of line \(PM\) is given by
\(\frac{{x – {x_1}}}{a} = \frac{{y – {y_1}}}{b} = \frac{{z – {z_1}}}{c}\)
Let \(\frac{{x – {x_1}}}{a} = \frac{{y – {y_1}}}{b} = \frac{{z – {z_1}}}{c} = r\)
Thus, the coordinates of any point on this line are \(\left( {{x_1} + ar,{y_1} + br,{z_1} + cr} \right),\) where \(r\) is a real number.
Now, the point \(M\) lies on line \(PM\).
So, the coordinates of point \(M\) is of the form, \(\left( {{x_1} + ar,{y_1} + br,{z_1} + cr} \right),\) and it will satisfy the equation of the plane.
\(\therefore a\left( {{x_1} + ar} \right) + b\left( {{y_1} + br} \right) + c\left( {{z_1} + cr} \right) + d = 0\)
\( \Rightarrow r = – \frac{{\left( {a{x_1} + b{y_1} + c{z_1} + d} \right)}}{{{a^2} + {b^2} + {c^2}}}….\left( {ii} \right)\)
Using the distance formula,
\(PM = \sqrt {{{\left( {{x_1} + ar – {x_1}} \right)}^2} + {{\left( {{y_1} + br – {y_1}} \right)}^2} + {{\left( {{z_1} + cr – {z_1}} \right)}^2}} \)
\( \Rightarrow PM = \sqrt {{a^2} + {b^2} + {c^2}} \times \left| r \right|\)
\( \Rightarrow PM = \sqrt {{a^2} + {b^2} + {c^2}} \left| {\frac{{ – \left( {a{x_1} + b{y_1} + c{z_1} + d} \right)}}{{{a^2} + {b^2} + {c^2}}}} \right|\) [From \(\left( {ii} \right)\)]
\(\therefore PM = \frac{{\left| {a{x_1} + b{y_1} + c{z_1} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Solved Examples on Distance of a Point from a Line \(3D:\)

Q.1. Find the distance of the point \(2\hat i + \hat j – \hat k\) from the plane \(\vec r \cdot (\hat i – 2\hat j + 4\hat k) = 9\).
Ans: Perpendicular distance, \(p = \frac{{|\vec a \cdot \vec n – d|}}{{|\vec n|}}\)
Here, \(\vec a = 2\hat i + \hat j – \hat k,\vec n = (\hat i – 2\hat j + 4\hat k)\) and \(d = 9\)
Thus, the required distance, \(p = \frac{{|(2\hat i + \hat j – \hat k) \cdot (\hat i – 2\hat j + 4\hat k) – 9|}}{{\sqrt {1 + 4 + 16} }}\)
\( = \frac{{|(2\hat i + \hat j – \hat k) \cdot (\hat i – 2\hat j + 4\hat k) – 9|}}{{\sqrt {1 + 4 + 16} }}\)
\(p = \frac{{13}}{{\sqrt {21} }}\) units.

Q.2. Find the equations of the planes parallel to the plane \(x – 2y + 2z – 3 = 0\) which is at a unit distance from the point \(\left( {1,2,3} \right).\)
Ans: Let the equation of a plane parallel to the plane \(x – 2y + 2z – 3 = 0\) be
\(x – 2y + 2z + k = 0…..\left( i \right)\)
Now, the distance of the plane \(x – 2y + 2z + k = 0\) from the point \(\left( {1,2,3} \right)\) is given by
\(\left| {\frac{{1 – 2 \times 2 + 2 \times 3 + k}}{{\sqrt {{1^2} + {{( – 2)}^2} + {2^2}} }}} \right| = \left| {\frac{{k + 3}}{3}} \right|\)
According to the question, we have
\(\left| {\frac{{k + 3}}{3}} \right| = 1\)
\( \Rightarrow k + 3 = \pm 3\)
\( \Rightarrow k = 0\) or \(k = – 6\)
Putting the values of \(k\) in (i), we obtain
\(x – 2y + 2z = 0\) and \(x – 2y + 2z – 6 = 0\) as the equations of the required planes.

Q.3. Find the distance between the point \(P\left( {6,5,9} \right)\) and the plane determined by the points \(A\left( {4, – 1,2} \right),B\left( {5,2,4} \right)\) and \(C\left( { – 1, – 1,6} \right).\)
Ans: We know that the equation of a plane passing through \(A\left( {3, – 1,2} \right)\) is given by
\(a\left( {x – 4} \right) + b\left( {y + 1} \right) + c\left( {z – 2} \right) = 0…\left( i \right)\)
Now, if the plane passes through the points \(B\left( {5,2,4} \right)\) and \(C\left( { – 1, – 1,6} \right),\) then the coordinates of these points must satisfy equation \((i)\)
Thus, we have \(a\left( {5 – 4} \right) + b\left( {2 + 1} \right) + c\left( {4 – 2} \right) = 0\)
\( \Rightarrow a + 3b + 2c = 0…\left( {ii} \right)\)
And,
\(a\left( { – 1 – 4} \right) + b\left( { – 1 + 1} \right) + c\left( {6 – 2} \right) = 0\)
\(a\left( { – 5} \right) + b\left( 0 \right) + c\left( 4 \right) = 0\)
\( \Rightarrow – 5a + 0\,b + 4c = 0…..\left( {iii} \right)\)
Now, solving equations \(\left( {ii} \right)\) and \(\left( {iii} \right),\)
\(\frac{a}{{12}} = \frac{b}{{ – 14}} = \frac{c}{{15}} = k\)
\( \Rightarrow a = 12k\)
\( \Rightarrow b = – 14k\)
\( \Rightarrow c = 15k\)
Substituting the values of \(a,b,c\) in \(\left( i \right),\) we obtain
\(12\left( {x – 4} \right) – 14\left( {y + 1} \right) + 15\left( {z – 2} \right) = 0\)
\( \Rightarrow 12x – 14y + 15z = 92\)
Thus, the equation of the plane passing by the points
\(A\left( {4, – 1,2} \right),B\left( {5,2,4} \right)\) and \(C\left( { – 1, – 1,6} \right)\) is \(12x – 14y + 15z = 92\)
Now, the distance of the point \(P\left( {6,5,9} \right)\) from plane \(12x – 14y + 15z = 92\) is
\( = \left| {\frac{{12\left( 6 \right) – 14\left( 5 \right) + 15\left( 9 \right)}}{{\sqrt {144 + 196 + 225} }}} \right|\)
\( = \frac{{137}}{{\sqrt {565} }}\)
\(\therefore \) Distance \( = 5.763\,{\text{units}}.\)

Q.4. If the coordinate axes in points \(A,B,\) and \(C\) are intersected by a variable plane at a constant distance \(p\) from the origin.Through these points, planes are drawn parallel to the coordinate planes. Show that the locus of the point of intersection is \(\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} + \frac{1}{{{z^2}}} = \frac{1}{{{p^2}}}.\)
Ans: Let the variable plane be \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)
It cuts the coordinate axes at \(A\left( {a,0,0} \right),B\left( {0,b,0} \right)\) and \(C\left( {0,0,c} \right)\) and it is at a distance \(p\) from the origin.
\(\therefore \frac{{\frac{0}{a} + \frac{0}{b} + \frac{0}{c} – 1}}{{\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }} = p\)
\( \Rightarrow \frac{1}{{\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }} = p\)
\( \Rightarrow \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{1}{{{p^2}}}….\left( i \right)\)
Let \(P\left( {\alpha ,\beta ,\gamma } \right)\) be the point of intersection of planes through \(A\left( {a,0,0} \right),B\left( {0,b,0} \right)\) and \(C\left( {0,0,c} \right),\) and parallel to \(yz,zx\) and \(xy\)-planes respectively.
The equations of planes passing through \(A\left( {a,0,0} \right),B\left( {0,b,0} \right)\) and \(C\left( {0,0,c} \right)\) and parallel to \(yz,zx\) and \(xy\)- planes are \(x = a,y = b\) and \(z = c\) respectively.
These three planes intersect at the point \(\left( {a,b,c} \right)\)
\(\therefore \alpha = a,\beta = b\) and \(\gamma = c…..\left( {ii} \right)\)
Replacing \(a,b,c\) from \(\left( i \right)\) and \(\left( {ii} \right),\) we have
\({\alpha ^{ – 2}} + {\beta ^{ – 2}} + {\gamma ^{ – 2}} = {p^{ – 2}}\)
Hence, the locus of \(P\left( {\alpha ,\beta ,\gamma } \right)\) is \({x^{ – 2}} + {y^{ – 2}} + {z^{ – 2}} = {p^{ – 2}}.\)

Summary:

This article lists and explains the formulas to calculate the distance of a point from a line in \(2D,\) and \(3D\) in both cartesian and vector forms. The length of the perpendicular from a point \(\left( {{x_1},{y_1}} \right)\) to a line \(ax + by + c = 0\) is given by \(\left| {\frac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|.\) And, the length of the perpendicular from a point having position vector \(\vec a\) to the plane \(\vec r \cdot \vec n = d\) is \(p = \frac{{|\vec a \cdot \vec n – d|}}{{|\vec n|}}\). The derivation of all these formulas have been provided along with the solved examples for better understanding of the topic.

FAQs on Distance of a Point from a Line:

Q.1. How do you calculate the distance of a point from a line?
Ans: In \(2\) dimensions, let the equation of the line be \(ax + by + c = 0\) and let \(\left( {p,q} \right)\) be a point.
Then, the distance between the given point and the given line \( = \frac{{\left| {ap + bq + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)
In \(3\) dimensions, let the point \( = \left( {p,q,r} \right)\) and a plane \(ax + b + cz + d = 0.\)
Then, the distance between the point and the plane \( = \frac{{\left| {ap + bq + cr + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Q.2. What is the distance from a point to a line?
Ans: According to Euclidean geometry, the shortest distance between the point and the nearest point that lies on the line is the length of the line segment connecting the point to the line. This is the perpendicular distance of the point to the line.

Q.3. What is the minimum distance from a point to the line segment using Vectors?
Ans: \(D = \frac{{\overrightarrow {AP} \times \vec d}}{{\vec d}}\)
where, \(D\) is the perpendicular distance
\(\vec d\) is the direction vector
\(P\) is the point \(\left( {{x_1},{y_1},{z_1}} \right)\)
\(A\) is any point on the line

Q.4. How do you find the distance between a point \(P\left( {3,4,5} \right)\) and the \(YZ\)-plane?
Ans: Let \(P\left( {x,y,z} \right)\) be a point in space. Then
Perpendicular distance of a point \(P\) from \(YZ\)-plane \( = \left| x \right|\,{\text{units}}\)
Perpendicular distance of a point \(P\) from \(XZ\)-plane \( = \left| y \right|\,{\text{units}}\)
Perpendicular distance of a point \(P\) from \(XY\)-plane \( = \left| z \right|\,{\text{units}}\)
Hence, the distance of the point \(P\left( {3,4,5} \right)\) from the \( = YZ\)-plane \( = 3\,{\text{units}}{\text{.}}\)

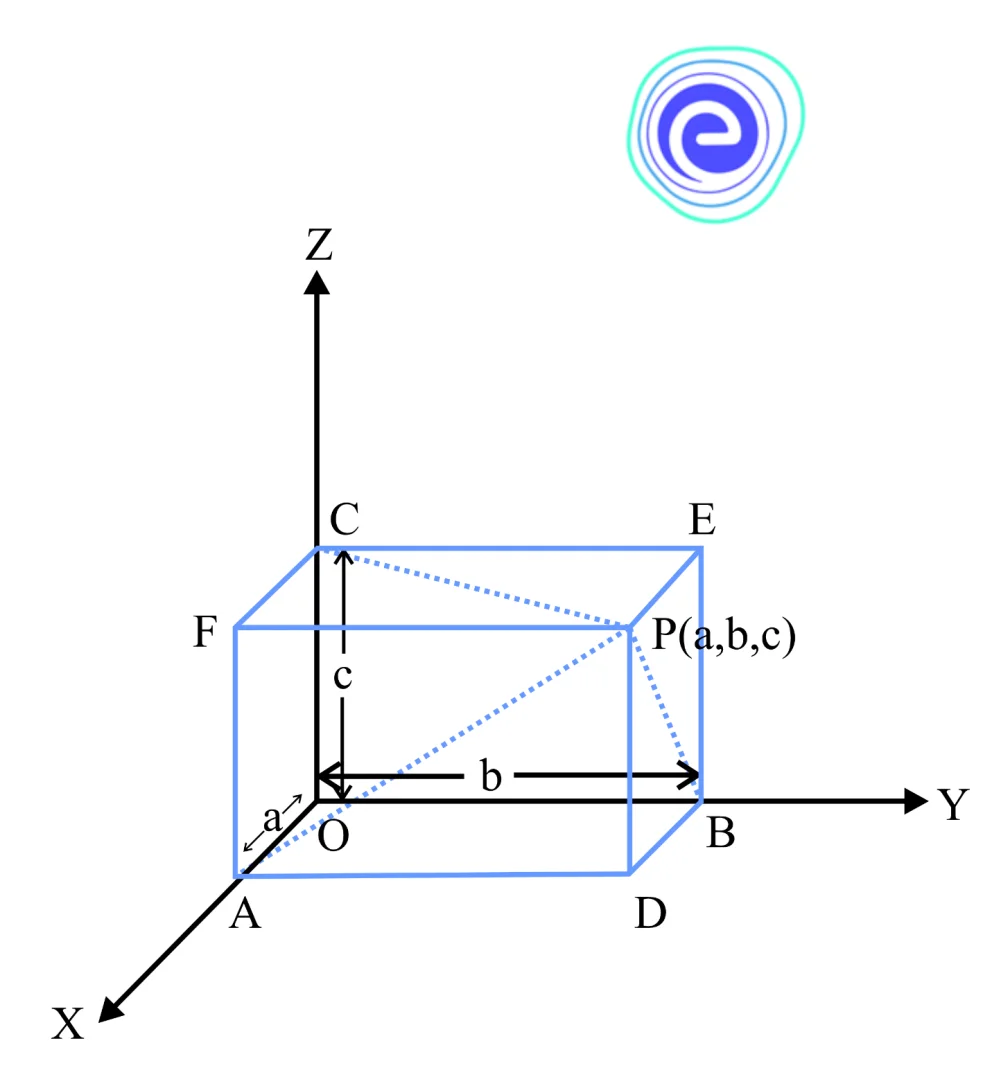
Q.5. In the \(XYZ\)-plane if the coordinates of a point \(P\) are \(\left( {a,b,c} \right)\) then find the perpendicular distance of \(P\) from the \(X\)-axis.
Ans: Consider the following figure

We observe that \(PA\) is the perpendicular distance of the point \(P\) from \(X\)-axis.
Using the Pythagoras theorem in \(\Delta APD,\) we have
\(A{P^2} = A{D^2} + P{D^2}\)
Since \(AD = OB = b,\) and \(PD = OC = c,\)
\(A{P^2} = {b^2} + {c^2}\)
Hence, \(AP = \sqrt {{b^2} + {c^2}} {\text{units}}\)

Hope this detailed article on Distance of a Point from a Line helps you in your preparation. In case of any query, reach out to us in the comment section and we will get back to you at the earliest.