Electrode Potential and Standard Electrode Potential

Electrode Potential and Standard Electrode Potential: Electrochemical cells are part and parcel of our everyday lives. Be it the lithium-ion batteries in our iPhones or the disposable AA batteries in our remote controls. These batteries are electrolytic cells that consist of two electrodes (a cathode and an anode). Both of these electrodes can be made of the same or different metals, immersed in an electrolyte in which the two electrodes are immersed. But how do these electrodes conduct electricity? This is because potential is developed across the electrodes that enable the flow of electrons. Let’s explore more about it in this article.

What is Electrode Potential? 

We know that there is a flow of current in an electrochemical cell. When a metal, such as copper, is placed in a solution of its ions, either of the three cases can happen-

a) The metal ions \({\rm{(C}}{{\rm{u}}^{{\rm{2 + }}}}{\rm{)}}\) may suffer a collision with the electrode and do not undergo any change. 

b) \({\rm{(C}}{{\rm{u}}^{{\rm{2 + }}}}{\rm{)}}\) ions may gain electrons from the electrode and get converted into metal atoms (i.e. the ions are reduced).

\({\rm{C}}{{\rm{u}}^{{\rm{2 + }}}} + 2{{\rm{e}}^ – } \to {\rm{Cu (Reduction)}}\)

c) The \({\rm{Cu}}\) atoms on the electrode may lose electrons to become \({\rm{(C}}{{\rm{u}}^{{\rm{2 + }}}}{\rm{)}}\) ions and go into the solution (i.e., oxidation occurs) 

\({\rm{C}}{{\rm{u}}^{{\rm{2 + }}}} + 2{{\rm{e}}^ – } \to {\rm{Cu (Oxidation)}}\)

If the metal atom has a relatively high tendency to get oxidised, it will go into the solution as ions and leave behind the electrons at the electrode. Due to the accumulation of electrons, the electrode acquires a slight negative charge with respect to the solution.

Similarly, there is a tendency of metal ions from the solution to take up electrons from the electrode and get deposited on the metal electrode as \({\rm{Cu}}\) atoms.

After some time, an equilibrium is established between \({\rm{Cu}}\) and \({\rm{(C}}{{\rm{u}}^{{\rm{2 + }}}}{\rm{)}}\) ions.

\({\text{Cu}} \rightleftharpoons {\text{C}}{{\text{u}}^{2 + }} + 2{{\text{e}}^ – }\)

At equilibrium, there is a separation of charges resulting in the electrode being positively or negatively charged with respect to the solution. As a result, a definite potential difference is developed between the metal and the electrode potential solution.

Similarly, when a zinc plate is immersed in a solution of \({\rm{Z}}{{\rm{n}}^{2 + }}\) ions, it becomes negatively charged with respect to the solution. Consequently, a potential difference is set up between the zinc plate and the solution which is known as the electrode potential of zinc.

The magnitude of the electrode potential of a metal is a measure of its relative tendency to undergo loss of electrons (oxidation) or gain of electrons (reduction).

Depending on the tendency of the metal electrode to lose or gain electrons, the electrode potential may be of two types:

1. Oxidation potential: Such an electrode tends to lose electrons or to get oxidised. Such an electrode is negatively charged with respect to solution and acts as the anode (oxidation).

\({\text{M}} \to {{\text{M}}^{{\text{n + }}}} + {\text{n}}{{\text{e}}^ – }\left( {{\text{Oxidation}}} \right)\)

2. Reduction potential: Such an electrode tends to gain electrons or to get reduced. Such an electrode is positively charged with respect to solution and acts as the cathode (reduction). 

\({{\rm{M}}^{{\rm{n}} + }} + {\rm{n}}{{\rm{e}}^ – } \to {\rm{M(Reduction)}}\)

The reduction potential is the reverse of oxidation potential. For example: If the reduction potential of \({\text{Zn}}\) is \(- 0.76\) volts, its oxidation potential \({\rm{ + 0}}.{\rm{76}}{\mkern 1mu} \,{\rm{volts}}.\)

The half cell reactions are always written as reduction half-reactions, and their potentials are represented as reduction potentials or electrode potentials. In an electrochemical cell, the electrons flow from the negative electrode to the positive electrode. The direction of current flow is opposite to that of electron flow. It is not possible to measure the potential of a single electrode directly.  It is, therefore, coupled with another electrode known as reference electrodes whose potential is known.

EMF of a Cell

Electrochemical cell comprises of two half cells that have different reduction potentials. This means they have a different tendency to lose or gain electrons. 

The electrode with a lower reduction potential will have a decreased tendency to gain electrons, whereas the electrode with a higher reduction potential will have an increased tendency to gain electrons. Consequently, a potential difference develops, and electrons flow from the electrode with a lower reduction potential (higher tendency to lose electrons) to the electrode with higher reduction potential (lower tendency to lose electrons).

Hence, the electromotive force or cell potential of a cell is the difference between the electrode potentials of the two electrodes constituting an electrochemical cell. The emf of a cell is expressed in volts.

The electrodes of an electrochemical cell are designated as the cathode (negative electrode) and the anode (positive electrode), where oxidation occurs at the anode and reduction occurs at the cathode.

\({\rm{e}}{\rm{.m}}{\rm{.f}}\,{\rm{ = }}\) Reduction potential of cathode \(-\) Reduction potential of anode \({{\rm{E}}_{{\rm{cell}}}} = {{\rm{E}}_{{\rm{right(cathode)}}}} – {{\rm{E}}_{{\rm{left(anode)}}}}\)

For example– let us consider a cell reaction as: \({\rm{Cu(s)}} + 2{\rm{A}}{{\rm{g}}^ + }({\rm{aq}}) \to {\rm{C}}{{\rm{u}}^{2 + }}({\rm{aq}}) + 2{\rm{Ag(s)}}\)

The half cell reactions:
Cathode (reduction): \({\rm{2A}}{{\rm{g}}^ + }({\rm{aq}}) + 2{{\rm{e}}^ – } \to 2{\rm{Ag(s)}}\)
Anode(oxidation): \({\rm{Cu(s)}} \to {\rm{C}}{{\rm{u}}^{2 + }}({\rm{aq}}) + 2{{\rm{e}}^ – }\)

The above equation shows that the silver electrode acts as a cathode and the copper electrode acts as an anode. The cell can be represented as-

\({\rm{Cu}}\left( {\rm{s}} \right){\mkern 1mu} /{\mkern 1mu} {\rm{C}}{{\rm{u}}^{{\rm{2  +  }}}}\left( {{\rm{aq}}} \right){\mkern 1mu} {\mkern 1mu} \left\| {{\rm{A}}{{\rm{g}}^ + }} \right.\left( {{\rm{aq}}} \right){\mkern 1mu} /{\mkern 1mu} {\rm{Ag}}\left( {\rm{s}} \right)\)

\({{\rm{E}}_{{\rm{cell}}}} = {{\rm{E}}_{{\rm{right}}({\rm{cathode}})}} – {{\rm{E}}_{{\rm{left}}({\rm{anode}})}} = {{\rm{E}}_{{\rm{A}}{{\rm{g}}^ + }/{\rm{Ag}}}} – {{\text{E}}_{{\text{C}}{{\text{u}}^{{\text{2 + }}}}{\text{/Cu}}}}\)

The e.m.f. of the cell depends upon:
1. The nature of the electrodes,
2. Temperature and
3. The concentrations of the solutions in the two half cells.

Standard Electrode Potential

The half cells in an electrochemical cell can not work independently; hence, it is impossible to determine the electrode’s reduction potential. The reduction potentials of the electrode can be determined by combining the electrodes with another electrode known as a reference electrode. The reduction potential of this electrode is arbitrarily set to zero. 

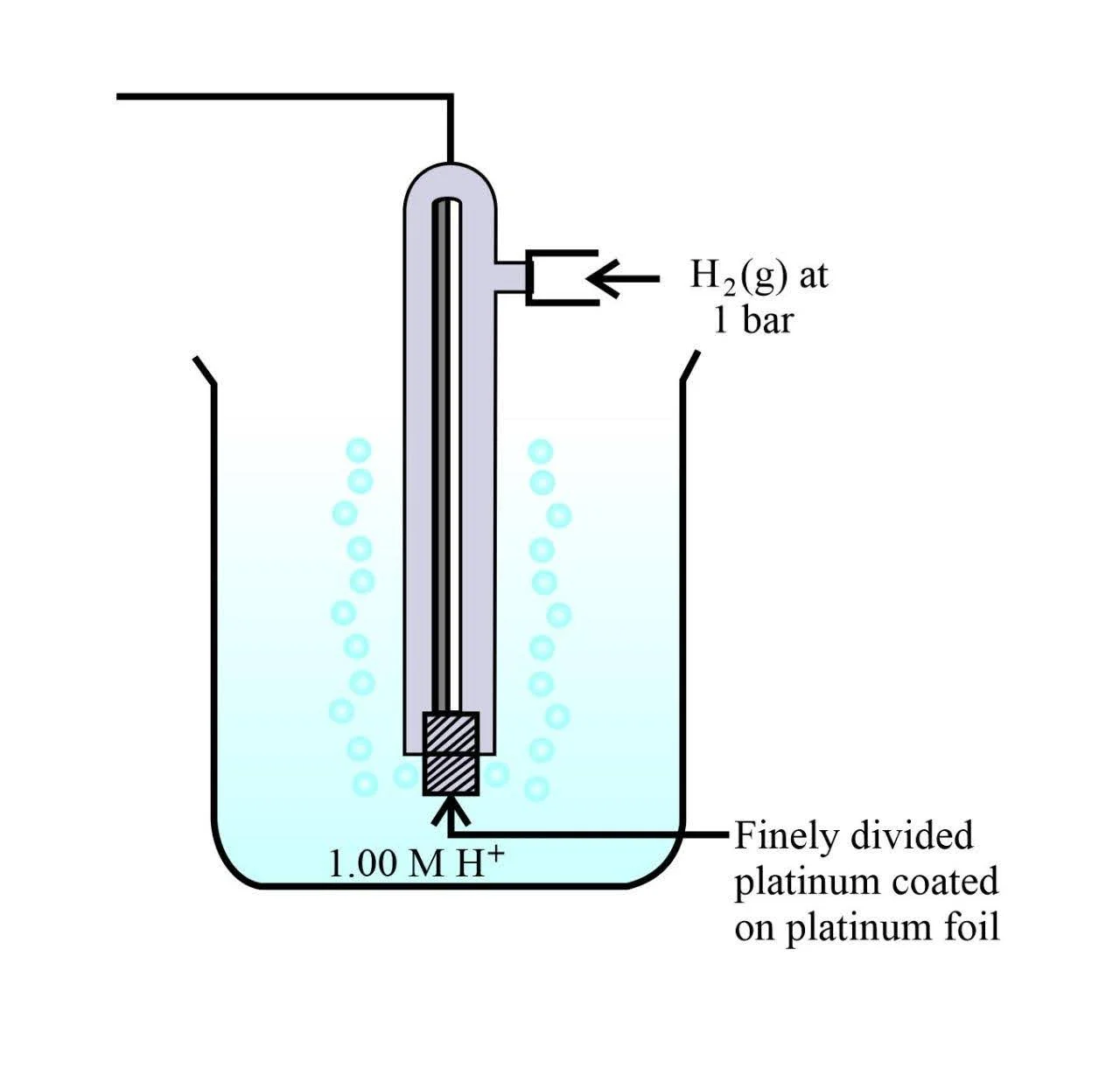
One of the universally accepted reference electrodes is the standard hydrogen electrode (SHE). It is also called a normal hydrogen electrode (NHE).

Standard Hydrogen Electrode

SHE consists of platinum wire sealed in a glass tube with a platinum foil attached to it. The platinum foil is coated with finely divided platinum that acts as the platinum electrode. The entire setup is dipped into an acidic solution containing \(1{\text{M}}\) hydrogen ion. At a constant temperature of \(298\,{\text{K}}\) and \(1\) bar (atmosphere) pressure, pure hydrogen gas is bubbled through it. The surface of the foil acts as a site for the reaction. 

According to the convention, the half-cell of standard hydrogen electrode is represented by:

\({\text{Pt}}\left( {\text{s}} \right)|{{\text{H}}_2}\left( {\text{g}} \right)/{{\text{H}}^ + }\left( {{\text{aq}}} \right)\)

If SHE acts as an anode-

\({{\rm{H}}_2}({\rm{g}}) \to 2{{\rm{H}}^ + }({\rm{aq}}) + 2{{\rm{e}}^ – }\)

If SHE acts as cathode-

\(2{{\rm{H}}^ + }({\rm{aq}}) + 2{{\rm{e}}^ – } \to {{\rm{H}}_2}({\rm{g}})\)

The reduction potential of any metal electrode can be determined by connecting the electrode with the standard hydrogen electrode.

Hence, the standard electrode potential is the reduction potential of a metal electrode which is determined with respect to a standard or normal hydrogen electrode. It can also be defined as the electrode potential of an electrochemical cell in which the concentrations of all the species involved in a half-cell is unity.

Measurement of the Standard Electrode Potential 

To measure the standard electrode potential of a metal electrode, the metal electrode is dipped in \(1.0\,{\rm{M}}\) solution of the electrolyte. This constitutes the metal-metal ion electrode or \({\rm{M/}}{{\rm{M}}^{{\rm{n}} + }}({\rm{aq}})\) electrode.

The \({\rm{M/}}{{\rm{M}}^{{\rm{n}} + }}({\rm{aq}})\) electrode is connected to the reference electrode (SHE) through a salt bridge. The electrodes are connected to a voltmeter to measure the e.m.f. of the cell. Hence, the standard electrode potential of the metal electrode is calculated.

Measurement of the Standard Electrode Potential of \({\rm{Z}}{{\rm{n}}^{2 + }}/{\rm{Zn}}\) Electrode

A zinc rod is immersed in a \({\rm{1M}}\) solution of \({\rm{ZnS}}{{\rm{O}}_4}\) and is combined with SHE. The SHE acts as a cathode, the zinc electrode acts as the anode, and the flow of electrons occurs from the zinc electrode to the hydrogen electrode. The cell may be represented as-

\({\rm{Zn}}\left( {\rm{s}} \right){\mkern 1mu} /{\mkern 1mu} {\rm{Z}}{{\rm{n}}^{{\rm{2  +  }}}}\left( {1{\mkern 1mu} {\rm{M}}} \right){\mkern 1mu} {\mkern 1mu} \left\| {{{\rm{H}}^ + }} \right.\left( {{\rm{1}}{\mkern 1mu} {\rm{M}}} \right){\mkern 1mu} /{\mkern 1mu} {{\rm{H}}_2}\left( {1{\mkern 1mu} {\rm{atm}}} \right),{\mkern 1mu} {\rm{Pt}}\)

The cell potential is measured to be \({\rm{0}}{\rm{.76 V}}\) Hence, the \({\rm{EMF}}\) of the cell is-

\({{\rm{E}}^0}_{{\rm{cell}}} = {{\rm{E}}^0}_{\rm{R}} – {{\rm{E}}^0}_{\rm{L}}\)

\({\text{E}}_{{\text{cell}}}^0 = {\text{E}}_{\left( {{{\text{H}}^ + }/{{\text{H}}_2}} \right)}^0 – {\text{E}}_{\left( {{\text{Z}}{{\text{n}}^{2 + }}/{\text{Zn}}} \right)}^0\)

\(0.76 = 0 – {\text{E}}_{\left( {{\text{Z}}{{\text{n}}^{{\text{2 + }}}}{\text{/Zn}}} \right)}^0\)

\({\text{E}}_{\left( {{\text{Z}}{{\text{n}}^{{\text{2 + }}}}{\text{/Zn}}} \right)}^0 = \, – 0.76\,{\text{V}}\)

Hence, the standard reduction potential of \({\left( {{\text{Z}}{{\text{n}}^{2 + }}/{\text{Zn}}} \right)}\) electrode is \( – 0.76\,{\rm{V}}\)

The negative value of the standard electrode potential indicates that hydrogen ions can oxidise zinc (or zinc can reduce hydrogen ions).

Measurement of the Standard Electrode Potential of \({\rm{C}}{{\rm{u}}^{2 + }}/{\rm{Cu}}\) Electrode

To measure electrode potential of \({\rm{C}}{{\rm{u}}^{2 + }}/{\rm{Cu}}\) electrode, a cell consisting of a copper electrode is immersed in \({\rm{1}}\,{\rm{M}}\,{\rm{CuS}}{{\rm{O}}_4}\) solution and is combined with SHE.

The SHE acts as the anode, the copper electrode acts as the cathode, and the flow of electrons takes place from SHE to the copper electrode.

Oxidation occurs at the hydrogen electrode, and reduction occurs at the copper electrode because hydrogen has a greater tendency to lose electrons than copper.

Thus, the cell may be represented as-

\({\text{Pt}},\,{{\text{H}}_2}\left( {1\,{\text{atm}}} \right)/{{\text{H}}^ + }\left( {1\,{\text{M}}} \right)\parallel {\text{C}}{{\text{u}}^{2 + }}\left( {1\,{\text{M}}} \right)/{\text{Cu}}\)

The cell potential is measured to be \({\rm{0}}{\rm{.34}}\,{\rm{V}}\) Hence, the EMF of the cell is-

\({{\rm{E}}^0}_{{\rm{cell}}} = {{\rm{E}}_{\rm{R}}}^0 – {{\rm{E}}^0}_{\rm{L}}\)

\({\rm{E}}_{{\rm{cell\;}}}^0 = {\rm{E}}_{\left( {{\rm{C}}{{\rm{u}}^{{\rm{2 + }}}}{\rm{/Cu}}} \right)}^0 – {\rm{E}}_{\left( {{{\rm{H}}^{\rm{ + }}}{{\rm{/H}}_{\rm{2}}}} \right)}^0\)

\({\text{E}}_{{\text{cell}}}^0{\text{ = E}}_{\left( {{\text{C}}{{\text{u}}^{{\text{2 + }}}}{\text{/Cu}}} \right)}^0 – {\text{E}}_{\left( {{{\text{H}}^{{\text{ + }}}}{\text{/}}{{\text{H}}_2}} \right)}^0\)

\({\text{E}}_{\left( {{\text{C}}{{\text{u}}^{{\text{2 + }}}}{\text{/Cu}}} \right)}^0 = 0.34\,{\text{V}}\)

Hence, the standard reduction potential of \(({\rm{C}}{{\rm{u}}^{2 + }}/{\rm{Cu}})\) electrode is \(0.34\,{\rm{V}}\).

The positive value of the standard electrode potential indicates that \({\rm{C}}{{\rm{u}}^{2 + }}\) ions get reduced more easily than \({{\rm{H}}^ + }\) ions. However, the \({{\rm{H}}^ + }\)  ions cannot oxidise \({\rm{Cu}}\)or hydrogen gas can reduce copper ions under standard conditions.

For Daniel Cell

\({\rm{Zn(s) + C}}{{\rm{u}}^{2 + }}({\rm{aq}}) \to {\rm{Z}}{{\rm{n}}^{2 + }}({\rm{aq}}) + {\rm{Cu(s)}}\)

Left electrode (anode) : \({\text{Zn}}\left( {\text{s}} \right) \to {\text{Z}}{{\text{n}}^{{\text{2 + }}}}\left( {{\text{aq}},\,1\,{\text{M}}} \right) + 2{{\text{e}}^ – }\)
Right electrode (cathode) : \({\rm{C}}{{\rm{u}}^{2 + }}({\rm{aq}},1{\rm{M) + 2}}{{\rm{e}}^ – } \to {\rm{Cu}}({\rm{s}})\)

\({{\rm{E}}^0}_{{\rm{cell}}} = {{\rm{E}}^0}_{\rm{R}} – {{\rm{E}}^0}_{\rm{L}} = 0.34\,{\rm{V – ( – 0}}{\rm{.76)V = 1}}{\rm{.10V}}\)

The standard hydrogen electrode is arbitrarily assigned zero; all other potentials are relative to the hydrogen half‐reaction. The table displays values of reduction potentials. For oxidation potentials, the sign is just reversed.

Inferences from the Standard Reduction Potential Table

1. If for an electrode, the standard electrode potential \( > \,0\) then its reduced form is more stable than the hydrogen gas.
2. If for an electrode, the standard electrode potential \( < \,0\), then its reduced form is more stable than hydrogen gas.
3. Fluorine ranks high in the table, which means fluorine gas is the strongest oxidising agent. The fluorine gas \(({{\rm{F}}_2})\) has the maximum tendency to get reduced to fluoride ions \(({{\rm{F}}^ – })\) Consequently, fluoride ion is the weakest reducing agent.
4. Lithium ranks lowest in the table, which means lithium-ion is the weakest oxidising agent. Consequently, lithium metal is the most powerful reducing agent in an aqueous solution.
5. As we move from top to bottom in the table, the standard electrode potential decreases. The oxidising power on the left-hand species decreases, and the reducing power of the species on the right-hand side of the reaction increases.

Summary

The story of electrochemistry begins with the invention of modern electrical batteries by Alessandro Volta. His invention led to major advances in understanding technology and addressed people’s industrial and daily life needs. All cells comprise an anode and cathode in which a spontaneous redox reaction takes place. The difference in potential energy between the anode and cathode governs the flow of electrons and is measured in units of volts. The flow of electrons occurs from the electrode having higher potential energy to the electrode having lower potential energy. Generally, the anode has higher potential energy; hence electrons move from anode to cathode. This page explains the concept of electrode potential and standard electrode potential. It also explains the measurement of standard electrode potential of \({\rm{C}}{{\rm{u}}^{2 + }}/{\rm{Cu}}\) and \({\rm{Z}}{{\rm{n}}^{2 + }}/{\rm{Zn}}\) electrode.

FAQs

Q.1. What is the difference between electrode potential and standard electrode potential?
Ans: The basic difference between single electrode potential and standard electrode potential is that the single electrode potential is the potential of a single electrode in an electrochemical cell, whereas standard electrode potential is the potential difference of the same electrode when combined with a reference electrode such as the standard hydrogen electrode. The reduction potential of SHE is arbitrarily assigned as zero.

Q.2. What is cell potential and electrode potential?
Ans: Electrode potential refers to the ability of an electrode in a cell to get reduced or oxidised. In contrast, cell potential represents the difference between the electrode potentials present in an electrochemical cell.

Q.3. Which electrode is used as a standard electrode?
Ans: A Standard Hydrogen Electrode (SHE) is used as a standard electrode or as a reference for all half-cell reactions. The value of the standard electrode potential is arbitrarily assigned as zero. The reduction potential of any metal electrode with reference to SHE is known as standard reduction potential.

Q.4. What is emf of cells?
Ans: The electromotive force or cell potential of a cell is the difference between the electrode potentials of the two electrodes constituting an electrochemical cell. The emf of a cell is expressed in volts.

Q.5. How do you calculate standard cell potential?
Ans:  From the reduction potential table, the potential of the oxidation half-reaction is obtained by the relation \({{\rm{E}}^0}_{{\rm{oxidation}}}\, =  \,- {{\rm{E}}^0}_{{\rm{reduction}}}\). The potentials of the half-cells are added to get the overall standard cell potential.

We hope this article on Electrode Potential and Standard Electrode Potential has helped you. If you have any queries, drop a comment below, and we will get back to you.