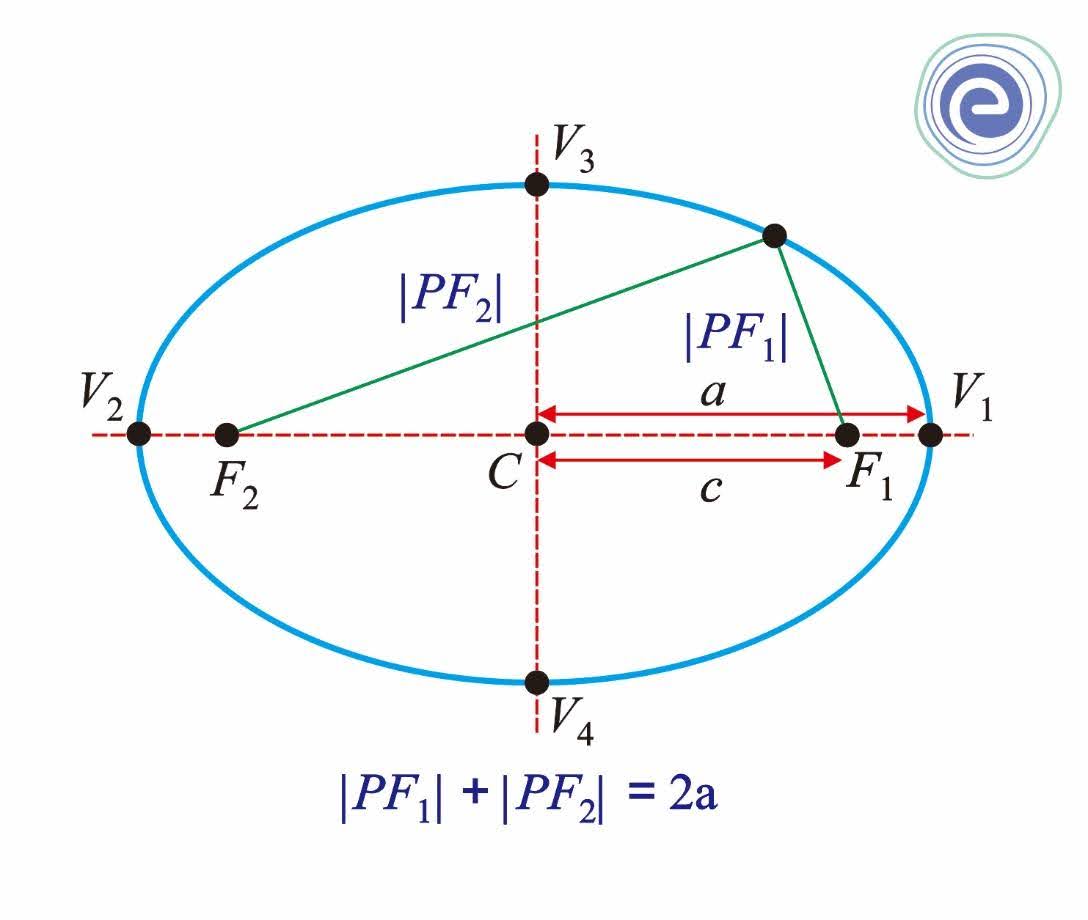
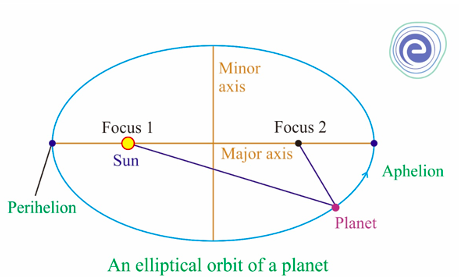
Ellipse: Do you know the orbit of planets, moon, comets, and other heavenly bodies are elliptical? Mathematics defines an ellipse as a plane curve surrounding two focal points in such a way that from any point on the curve, the sum of the distances to the two focal points is a constant. A circle is a special type of ellipse in which the two focal points are converged into one.

The elongation of an ellipse is measured by its eccentricity e {\displaystyle e} e, a number ranging from e=0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). This article discusses formulas and equations of an ellipse with solved ellipse examples. Read on to find out.

What is an Ellipse?

The locus of all points in a plane whose sum of distances from two fixed points in the plane is constant is called an Ellipse. The foci (singular focus) are the fixed points that are encircled by the curve. The constant is the eccentricity of an Ellipse, and the fixed line is the directrix. Eccentricity is a property of the Ellipse that indicates its lengthening and is symbolized by the letter \(e.\)

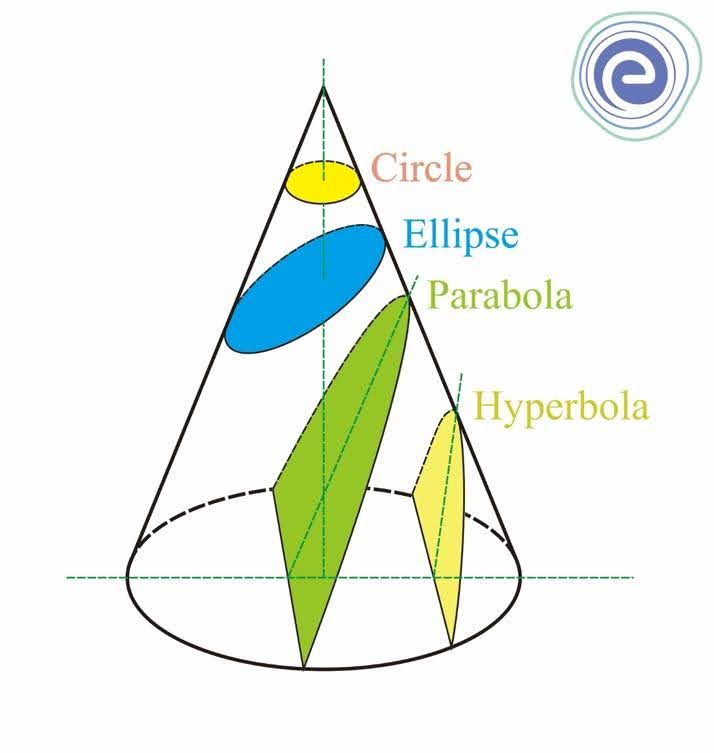
When a plane slices the cone at an angle with the base, the Ellipse is one of the conic sections that results. A circle is formed when the cone is intersected by a plane parallel to the base.

The various parts of an ellipse are described below:

(i) The Major axis is the line perpendicular to the directrix and passing through the focus.
(ii) The vertices are the point on the Ellipse where its major axis intersects.
(iii) The Centre is the midpoint of vertices of the Ellipse.
(iv) The Minor axis is the line perpendicular to the Major axis passing through the centre of the Ellipse.
(v) The chord that passes through any of the two foci and is perpendicular to the major axis is known as the Latus Rectum.

Ellipse Shape: Elliptical Meaning

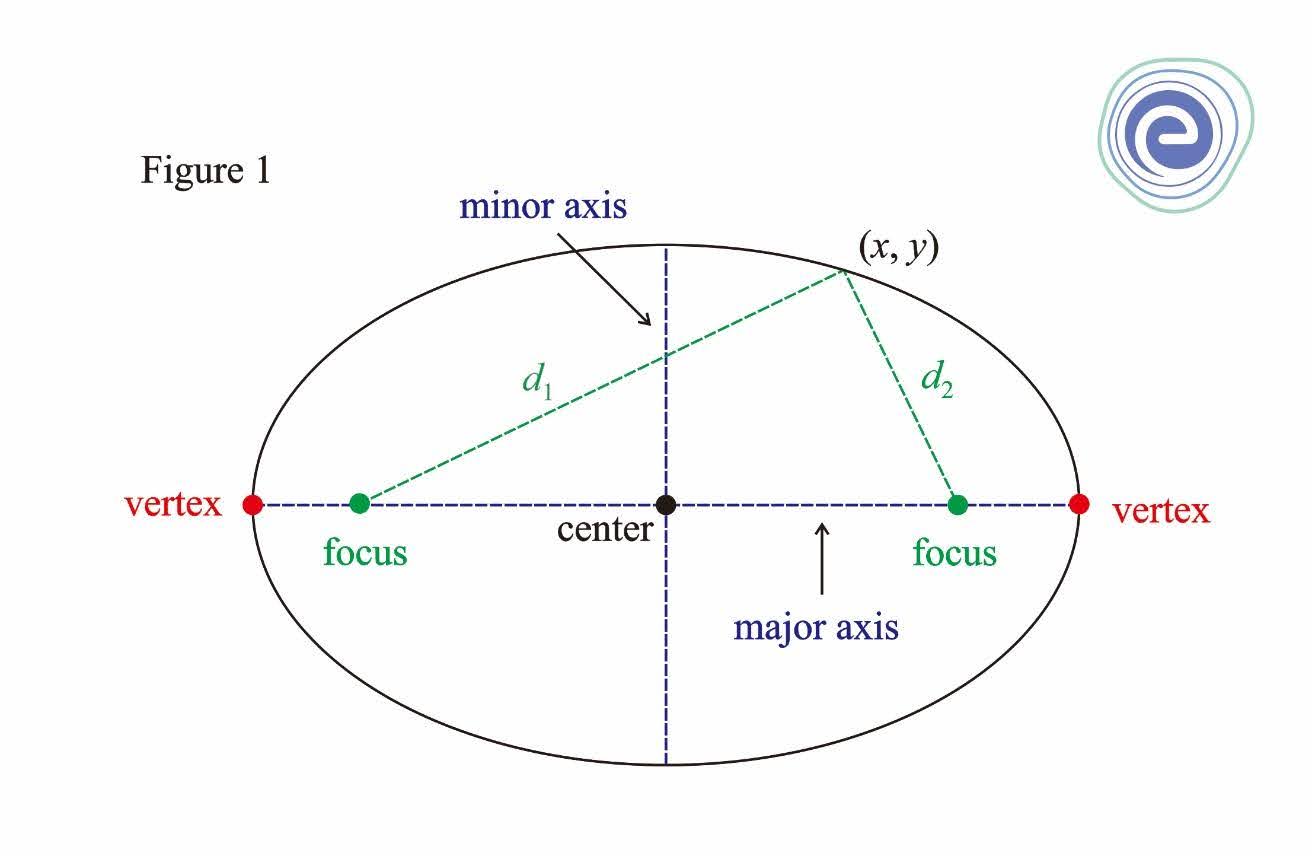
An ellipse is an oval or a squished circle approximately. An Ellipse is a geometrical figure that can be drawn in the sand. For that, first, push two sticks into the sand. Form a loop by taking a length of string large enough to fit around the two sticks and still have some slack. Take the third stick, hook it inside the string loop, pull the loop taut by pulling the third stick away from the first two sticks, then drag that third stick as far as the loop will allow into the sand. The shape resulted during this activity is an ellipse.

The word elliptical comes from the Ellipse, which is an oval shape. Many comets orbit the Sun in an elliptical orbit that brings them closer at times and farther away at others. The shape of an ellipse, which is an elongated circle stretched into an oval, is described by the term elliptical.

Ellipse Formulas

An Ellipse is a curve on a plane that contains two focal points such that the sum of distances for every point on the curve to the two focal points is constant. An Ellipse comprises two axes. They are the major axis and minor axis.

If the length of semi-major axis \( = a\) and length of semi-minor axis \( = b\), then

1. Area of the Ellipse \( = \pi ab\)
2. Perimeter of the Ellipse \( = 2\pi \sqrt {\frac{ { {a^2} + {b^2}}}{2}} \)
3. Equation of the Ellipse in standard form \( = \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

General Equation of Ellipse

The equation of Ellipse in the standard form is given by:

\( \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) for \(\left({a > b} \right),\)

Where,
\({b^2} = {a^2}\left({1 – {e^2}} \right)\)
\(e = \sqrt {1 – \frac{{{b^2}}}{{{a^2}}}} \)
Equation of Major axis \( = x\) axis
Equation of Minor axis \( = y\) axis
Centre \( = \left({0,\,0} \right)\)

Similarly, the equation of Ellipse, whose centre \((m,\,n)\) in the standard form is given by:

\(\frac{{{{\left({x – m} \right)}^2}}}{{{a^2}}} + \frac{{{{\left({y – n} \right)}^2}}}{{{b^2}}} = 1\)

On expanding the above equation, we get the general equation of an Ellipse, which looks like:

\(a {x^2} + 2hxy + b {y^2} + 2gx + 2fy + c = 0,\)

But the above expression will represent an Ellipse if \(\Delta \ne 0\) and \( {h^2} < ab\)
Where,
\(\Delta = \left| {\begin{array}{{c}} a & h & g \\ h & b & f \\ g & f & c \\ \end{array} } \right|\)

All the formulas and equations related to an ellipse are tabulated below:

Equation	\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\); \(a > b\)
Equation of Major axis	\(y = 0\)
Length of Major axis	\(2a\)
Equation of Minor axis	\(x = 0\)
Length of Minor axis	\(2b\)
Vertices	\(\left({ \pm a,\,0} \right)\)
Foci	\(\left({ \pm ae,\,0} \right)\)
Directrix	\(x = \pm \frac{a}{e}\)
Eccentricity	\(e = \sqrt {1 – \frac{{{b^2}}}{{{a^2}}}} \)
Length of a Latus-rectum	\(\frac{ {2 {b^2}}}{a}\)
Centre	\((0,\,0)\)
Focal distances of any point \(x,\,y\)	\(a \pm ex\)

What are the Properties of an Ellipse Conic Section?

Some of the important properties of an Ellipse are as follows:

1. Eccentricity is a conic section factor that indicates how round the conic section is. More eccentricity indicates less spherical behaviour, while less eccentricity indicates more spherical behaviour. It is symbolised by the letter “\(e.\)” The ratio of the distance between the focus and a point on the plane to the vertex and that point only is the eccentricity of the Ellipse. An Ellipse has an eccentricity, \(0 \leqslant e < 1.\)
2. There are two focal points, or foci, in every Ellipse. The total of the distances between the two foci at each point on the Ellipse is a constant.
3. The directrix is a line that runs parallel to Ellipse’s minor axis and connects both Ellipse’s foci.
4. The major axis is perpendicular to the directrix.
5. The focus and the vertex are connected via the major axis.
6. At the vertices, the tangent is parallel to the directrix.
7. The length of the latus rectum is \(\frac{ {2 {b^2}}}{a}\) when \(a > b\)

What are the Applications of Ellipses in Real-life?

Some real-life applications of an Ellipse are as follows:

1. The orbits of planets, satellites, moons, and comets, as well as the shapes of boat keels, rudders, and some aviation wings, can all be represented by Ellipses.
2. A lithotripter is a medical device that generates sound waves to break up kidney stones using elliptical reflectors.
3. Whispering chambers are structures with elliptical domes that allow a person whispering at one focus to be clearly heard by someone standing at the opposite focus. Because of an Ellipse’s acoustic properties, this happens. A sound wave will be reflected off the elliptical dome and back to the other focus when it originates at one focus of a whispering chamber. Two people standing \(43\) feet apart at the foci of the whisper chamber at the Museum of Science and Industry in Chicago can hear each other whisper.
4. When you spin an Ellipse about its major axis, you get a football.
5. The path of each planet is an Ellipse having the Sun at one focus, according to Kepler’s first law of planetary motion.
6. In an elliptical pool, the Ellipse’s reflection property is important because if you hit the ball through one focus, it will reflect off the Ellipse and go into the hole at the other focus.

Ellipse Examples – Solved

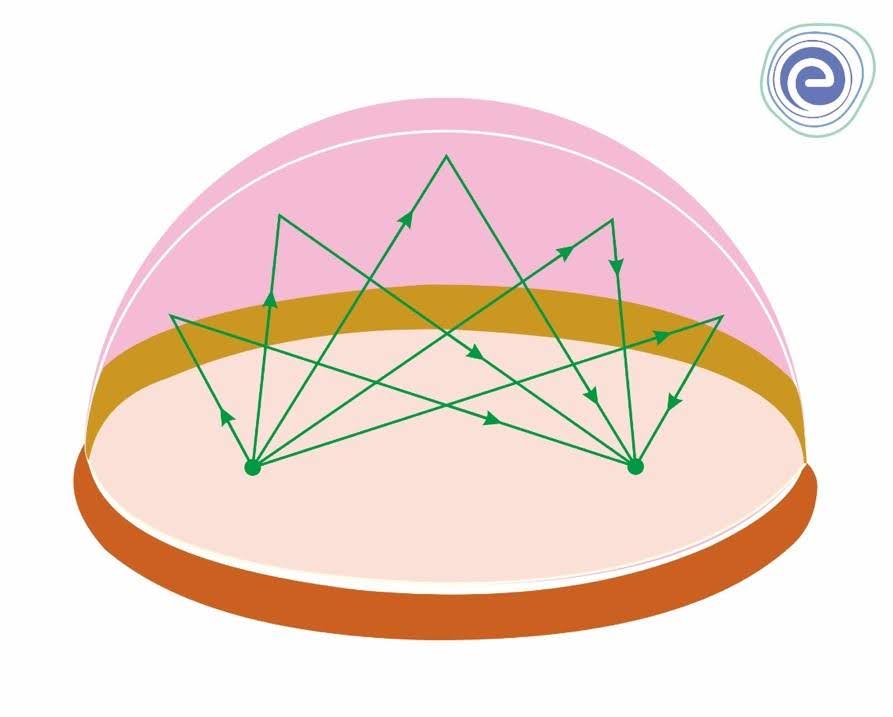
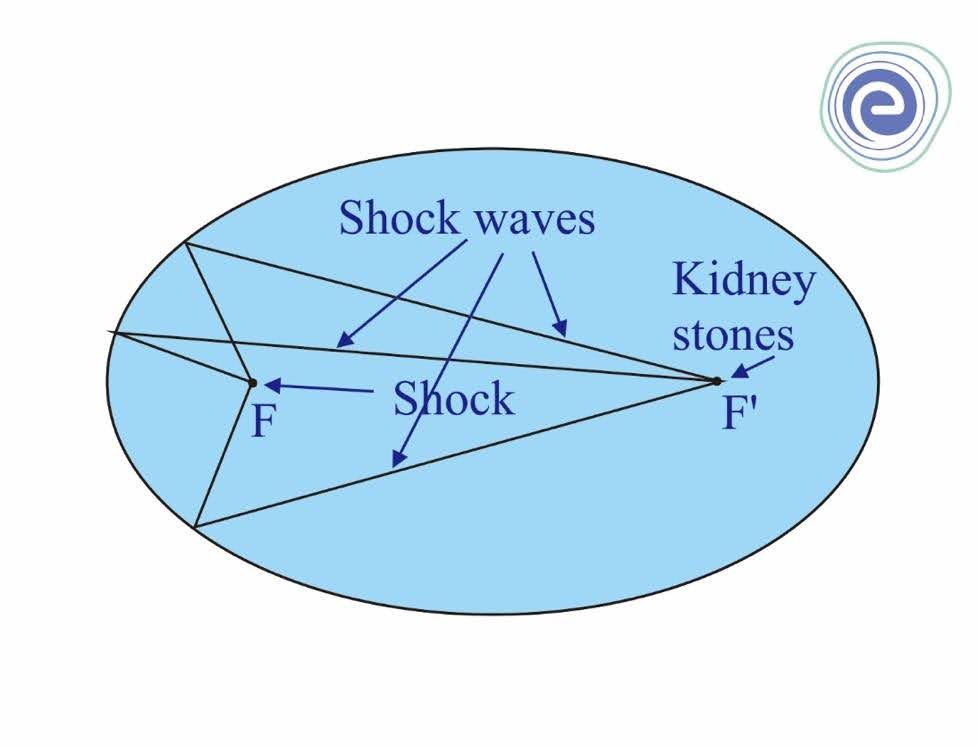
Q.1. What will be the sum of the focal distances of any point on the ellipse \(9 {x^2} + 16 {y^2} = 144\)?
Ans: Given \(9 {x^2} + 16 {y^2} = 144\)
\( \Rightarrow \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Here \(a=4\) and \(b=3\)
The sum of the distances of any point from their foci on an Ellipse is constant, which is the length of the major axis.
i.e. the sum of the focal distances of any point on an Ellipse \( = 2a = 8\)

Q.2. What will the eccentricity of Ellipse \(16 {x^2} + 25 {y^2} = 400\)?
Ans: Given \(16 {x^2} + 25 {y^2} = 400\)
\( \Rightarrow \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
Here \(a=5\) and \(b=4\)
So, \(e = \sqrt {1 – \frac{{{b^2}}}{{{a^2}}}} = \sqrt {1 – \frac{{16}}{{25}}} = \frac{3}{5}\)

Q.3. What will the coordinate of foci of Ellipse \(16 {x^2} + 25 {y^2} = 400\)?
Ans: Given \(16 {x^2} + 25 {y^2} = 400\)
\( \Rightarrow \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
Here \(a=5\) and \(b=4\)
So, \(e = \sqrt {1 – \frac{{{b^2}}}{{{a^2}}}} = \sqrt {1 – \frac{{16}}{{25}}} = \frac{3}{5}\)
So, coordinate of foci \( = \left({ \pm ae,\,0} \right) = \left({ \pm 3,\,0} \right)\)

Q.4. Find the length of the latus rectum of Ellipse \(9 {x^2} + 16 {y^2} = 144\)?
Ans: Given \(9 {x^2} + 16 {y^2} = 144\)
\( \Rightarrow \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Here \(a=4\) and \(b=3\)
So, The length of the latus rectum of Ellipse \( = \frac{{2{b^2}}}{a} = \frac{{2 \times 9}}{4} = \frac{9}{2}\)

Q.5. If the length of the major axis and minor axis of an Ellipse is \(10\) and \(8\) respectively, then find the eccentricity of that Ellipse?
Ans: Since the length of the major axis and minor axis of an Ellipse is \(10\) and \(8\), respectively.
So, \(2a = 10\), \(2b = 8\)
\(a = 5\), \(b = 4\)
So, \(e = \sqrt {1 – \frac{{{b^2}}}{{{a^2}}}} = \sqrt {1 – \frac{{16}}{{25}}} = \frac{3}{5}\)

Summary on Ellipse Conic Section

Ellipse is not simply about mathematics or how we plot an Ellipse. Ellipse has its own significance, which only a few understand, significance that can produce something extraordinary, and significance that can delight others with its beauty and uniqueness in buildings. We have seen its immense uses in the real world, which led to a significant role in the mathematical world.

Frequently Asked Questions on Ellipse

The most frequently asked questions about ellipses are answered here:

Q.1: What is an Ellipse in real life?
Ans: The orbits of planets, satellites, moons, and comets, as well as the shapes of boat keels, rudders, and some aviation wings, can all be represented by Ellipses. A lithotripter is a medical device that generates sound waves to break up kidney stones using elliptical reflectors.

Q.2: Is an Ellipse a circle?
Ans: Ellipses come in a variety of shapes, ranging from very broad and flat to virtually circular, depending on how far apart the foci are. The Ellipse becomes a circle when the two foci are in the same place.

Q.3: What is the best definition of an Ellipse?
Ans: The locus of all those locations in a plane whose sum of distances from two fixed points in the plane is constant is called an Ellipse. The foci (singular focus) are the fixed points that are encircled by the curve. The constant is the eccentricity of the Ellipse, and the fixed line is the directrix. Eccentricity is a property of the Ellipse that indicates its lengthening and is symbolised by the letter \(e\).

Q.4: What is Ellipse in English?
Ans: Ellipse in English has a different meaning. A punctuation mark consisting of three dots is known as an ellipsis (plural is Ellipses). When removing a word, phrase, line, paragraph, or more from a quoted passage, use an ellipsis. Ellipses help to save space by removing unimportant information.

Q.5: What is an elliptical shape?
Ans: The shape of an Ellipse, which is an elongated circle stretched into an oval, is described by the term elliptical. This term is also used to describe a method of speech that eliminates extraneous words. When writers utilise an elliptical style, the work might become obfuscated and difficult to understand.

We hope that our article on ellipses was useful for you. If you have any query or feedback to share with us, please feel to drop a comment below. We will get back to you at the earliest. In the end, we are winding up this article with best wishes for your exams on behalf of Embibe.