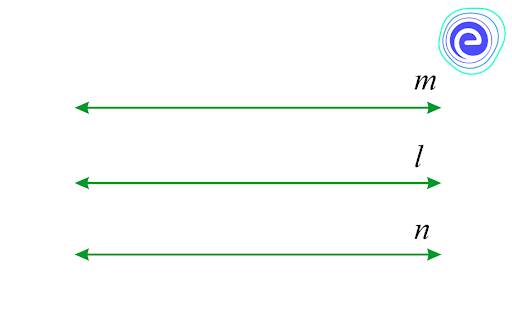Euclid’s Definitions, Axioms and Postulates With Diagram, Example

Euclid’s Definitions, Axioms and Postulates: Euclid was the first Greek mathematician who initiated a new way of thinking about the study of geometry. He introduced the method of proving the geometrical result by deductive reasoning based on previous results and some self-evident specific assumptions called axioms. Let’s learn about the definitions, axioms, and postulates proposed by Euclid in geometry.

Introduction to Euclid’s Geometry

The word ‘geometry’ is derived from the Greek words “geo”, meaning “earth”, and “metron”, meaning measuring. Thus, the word geometry means the measurement of the earth. Ancient Egyptians were the first people to study geometry. They were mainly concerned with finding the areas of plane figures such as triangles, rectangles etc., later. The Babylonians discovered formulae for finding the areas of various rectilinear figures.

The knowledge of geometry passed from the Egyptians to the Greeks, and many Greek mathematicians worked on geometry. Thale and his pupil Pythagoras were among them. Euclid was the first Greek mathematician who initiated a new way of thinking about the study of geometry. He introduced the method of proving the geometrical result by deductive reasoning based upon previously proved results and some self-evident specific assumptions known as axioms.

The geometry of plane figures is also based upon the approach of deductive logic. That is why it is popularly called Euclid’s geometry.

Define Axioms and Postulates

Axioms: Axioms are the basic facts that are taken for granted without proof. Sometimes axioms are intuitively evident, as is clear from the following examples:
Halves of equality are equal
\(a > b\) and \(b > c \Rightarrow a > c.\)
The whole part is equal to the sum of its parts and greater than any of its parts. In the development of plane geometry, we make some axioms and then deduce results by logical reasoning.

Theorems: The conclusion obtained through logical reasoning based on previously proved results and some axioms constitute a statement known as a theorem or a proposition.

Some undefined terms: There are three basic concepts in geometry: ‘ point’, ‘line’ and ‘plane’. It is not possible to define these three concepts precisely. We can, however, have a good idea of these concepts by considering examples as given below.

Point: The point is shown by a fine dot made by a sharp pencil on paper. In our subsequent discussion, we shall denote a point by a capital letter \(A,B,P,Q,R\) etc.
Thus, \(P\) is a point, as shown in the given diagram.

Plane: The surface of a smooth wall, a sheet of paper, or the surface of a smooth blackboard are comparative examples of a plane. The surface mentioned above is limited in extent, but the geometrical plane extends endlessly in all directions.

Line: If you fold the piece of paper, the crease in the paper represents a geometrically straight line. The edge of the ruler, the edge of the top of a table, the meeting place of two walls of a room are also examples of a geometrically straight line.

The straight line drawn on a sheet of paper with the help of a ruler and a sharp pencil is a comparative example of a geometrically straight line. A geometrical straight line is a collection of points and extends endlessly in both directions. To emphasize this point, we use two arrowheads at each end of a line drawn on a sheet of paper or a blackboard, as shown in the diagram.

Remark 1: In the above discussion, we have tried to explain the meanings of a point, line, and plane. But it is impossible to find exact examples of a point, a line or a plane. However, for practical purposes, we deal with close examples.

Remark 2: In theoretical terms, a plane and a line consist of sets of points and lines drawn in a plane are subsets of it.

Euclid’s Axioms and Postulates

We will see all the axioms and postulates given by Euclid in the following sections:

Seven Axioms of Euclid

The seven axioms of Euclid are given below:

1. Things that are equal to the same thing are equal to each other.
2. If equals are added to the equals, then the wholes are similar.
3. If equals are subtracted from the equals, then the remainders are similar.
4. The things that coincide with each other are equal.
5. The whole is larger than the part.
6. Things that are double of the same things are equal to each other.
7. Things that are halves of the same things are equal to each other.

Euclid’s Five Postulates

Below, you can see Euclid’s five postulates:

Postulate 1: The straight line can be drawn from any one point to any other point.

This postulate tells you that at least one straight line crosses two distinct points, but it does not say that there cannot be more than one line. However, in his work, Euclid has frequently assumed, without mentioning, that there is a unique line that is joining two distinct points. You can state this result in the form of an axiom as follows:

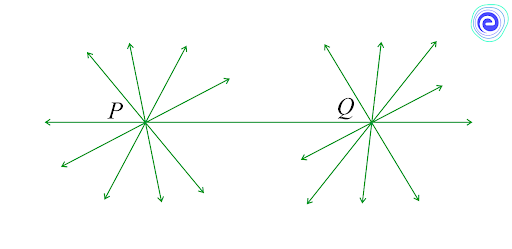
Axiom: Given two distinct points, there is a unique line that passes through them.

How many lines passing through \(P\) also pass through \(Q\) on the given diagram. Only one, that is, the line \(PQ.\) How many lines passing through \(Q\) also pass through \(P\)? Only one, that is, the line \(PQ.\) Hence, the statement that is given above is self-evident, and it is considered as an axiom.

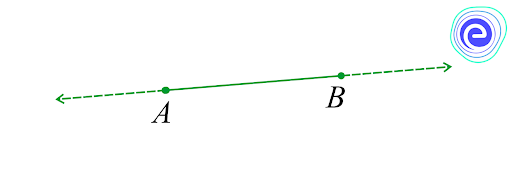
Postulate 2: A terminated line can be produced indefinitely.

Note that what you call the line segment nowadays is what Euclid called a terminated line. So, according to the present-day terms, the second postulate says that a line segment can be extended on either side to form a line in the given diagram.

Postulate 3: A circle can be drawn with any centre and radius.

Postulate 4: All the right angles are similar (equal) to one another.

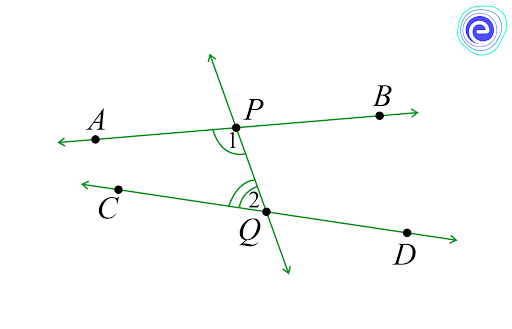
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it is taken together less than two right angles, then the two straight lines, if it is produced indefinitely, they meet on that side on which the sum of angles is less than the two right angles.

Example: The line \(PQ\) in the given diagram falls on lines \(AB\) and \(CD\) such that the sum of the interior angles \(1\) and \(2\) is less than \({180^ \circ }\) on the left side of \(PQ.\) Therefore, the lines \(AB\) and \(CD\) will eventually intersect on the left side of \(PQ.\)

Solved Examples: Euclid’s Definitions, Axiom and Postulates

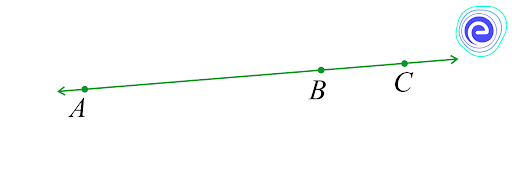
Q.1. If \(A,B\) and \(C\) are three points on a line, and \(B\) lies between \(A\) and \(C\) in the given diagram, then prove that \(AB + BC = AC.\)

Ans: In the given diagram above, \(AC\) coincides with \(AB + BC\)
Also, Euclid’s Axiom \(\left( 4 \right)\) says that things that coincide with one another are equal.
So, it can be deduced that
\(AB + BC = AC\)
Note that in the given solution, it has been considered that there is a unique line that is passing through two points.

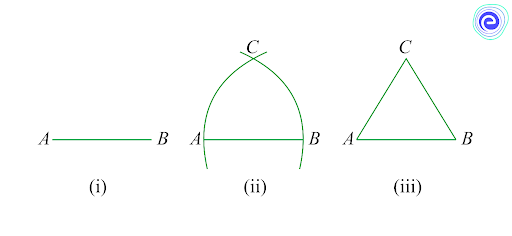
Q.2. Prove that an equilateral triangle may be constructed on any of the given line segments.
Ans: In the segment above, a line segment of any length is given, say \(AB,\) in the given diagram.

Here, you have to do some construction. Using Euclid’s postulate \(3,\) you can draw a circle with point \(A\) as the centre and \(AB\) as the radius in the given diagram. Similarly, you draw another circle with point \(B\) as the centre and \(BA\) as the radius. The two circles that meet at a point say \(C.\)

Now, draw the line segments \(AC\) and \(BC\) to form \(\Delta ABC\) in the given diagram.
So, you have to show that this triangle is the equilateral triangle, i.e., \(AB = AC = BC.\)
Now, \(AB = AC,\) since they are the radii of the same circle \(\left( 1\right)\)
Similarly, \(AB = BC\) (Radii of the same circle) \(\left( 2\right)\)
From the given two facts, and Euclid’s axiom that things that are equal to the same thing are equal, you can conclude that \(AB = BC = AC\)
So, \(\Delta ABC\) is an equilateral triangle.

Q.3. Prove that two lines that are both parallel to the same line are parallel to each other.
Ans: Three lines, \(l,m\) and \(n\) in a plane such that \(m||l\) and \(n||l.\)
Prove: \(m||n\)
If possible, let \(m\) be not parallel to \(n.\) Then, \(m\) and \(n\) intersect in a unique point, say \(p.\)

Thus, through a point \(p\) outside \(l,\) two lines \(m\) and \(n,\) both parallel to \(l.\) This is a contradiction to the parallel axiom. So, the supposition is wrong.
Hence, \(m||n\)

Q.4. Prove that two distinct lines cannot have more than one point in common.
Ans: Here, we are given two lines \(l\) and \(m.\) You need to prove that they have only a single point in common. Let us assume that the two lines intersect in two distinct points, say \(P\) and \(Q.\) So, you have two lines that are passing through two distinct points \(P\) and \(Q.\)
But this assumption clashes with the axiom that only one line can pass through two distinct points. So, the assumption that we started with that two lines can pass through two distinct points is wrong.
From this, we understand that we are forced to conclude that two distinct lines cannot have more than one point in common.

Q.5. If lines \(AB,AC,AD\) and \(AE\) are parallel to line \(l,\) then prove that points \(A,B,C,D\) and \(E\) are collinear.
Ans: Lines \(AB,AC,AD\) and \(AE\) are parallel to a line \(l.\)
Prove: \(A,B,C,D,\) and \(E\) are collinear.
Since lines \(AB,AC,AD\) and \(AE\) are parallel to a line \(l.\)
Therefore, point \(A\) lies outside \(l;\) and through \(A,\) lines \(AB,AC,AD\) and \(AE\) are drawn, each parallel to \(l.\) But, by parallel axiom, only one line can be drawn parallel to \(l,\) through a point outside it.
Therefore, the points \(A,B,C,D,E\) lie on the same line.
Hence, points \(A,B,C,D\) and \(E\) are collinear points.

Summary

In the given article, you can see the introduction of Euclid’s geometry, axioms, postulates, and example. We have covered Euclid’s seven axioms and five postulates, along with examples. We have also provided the solved examples along with a few FAQs.

FAQs

Q.1. What are the seven axioms of Euclid?
Ans: The seven axioms of Euclid are given below:
1. The things that are similar to the same thing are equal to each other.
2. If equals are added to the equals, then the wholes are similar.
3.If equals are subtracted from the equals, then the remainders are similar.
4. The things that coincide with each other are equal.
5. The whole is larger than the part.
6. The things that are double of the same things are similar (equal) to each other.
7. Things that are halves of the same things are equal to each other.

Q.2. What is the difference between axioms and postulates?
Ans: Axioms and postulates are essentially the same things. In math, the truths are accepted without proof. Axioms are general statements about real numbers. Sometimes they are called algebraic postulates. However, only a little difference between them is that the postulates are used for universal truths in geometry, and axioms are used everywhere. Though, both mean the same thing.

Q.3. What are the five postulates of Euclid?
Ans: Euclid’s five postulates are given below:
Postulate 1: A straight line can be drawn from any point to any other point.
Postulate 2: A terminated line can be produced indefinitely.
Postulate 3: The circle can be drawn with any centre and radius.
Postulate 4: All the right angles are similar to one another.
Postulate 5: If the straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Q.4. What is an axiom example?
Ans: A statement that is taken to be accurate so that further reasoning can be done is called an axiom. It is not something we want to prove.
Example: One of Euclid’s axioms is: “If \(A\) and \(B\) are two numbers that are similar, and \(C\) and \(D\) are also similar, \(A + C\) is the same as \(B + D\)”

Q.5. What are axioms, postulates and theorems?
Ans: Axioms or postulates are the assumptions that are apparent universal truths. They are not proven. Theorems are statements that are proved using definitions, axioms, previously proved statements and deductive reasoning.

Q.6. What is an axiom in math?
Ans: In math or logic, an axiom is an unprovable rule or the first principle accepted as true because it is self-evident or beneficial.
“Nothing can both be and cannot be at the same time and in the same respect” is an example of an axiom.

Learn All About Euclid’s Division Lemma

Now you are provided with all the necessary information on Euclid’s definitions, axioms and postulates and we hope this detailed article is helpful to you. If you have any queries regarding this article, please ping us through the comment section below and we will get back to you as soon as possible.