Family of Lines: Definition, Types, Characteristics, Equations, Examples

Family of lines: We know or meet different types of families in our lives. As a matter of fact, each family has some unique feature, and this feature is common to all the members in that family. For example, a family may have similar facial features, while another family may have all athletes or foodies. What would you think would be the feature of a family of lines in Mathematics?

In this article, let us learn about what constitutes a family of lines and their similar features.

What is a Family of Lines?

A set of lines that have at least one common feature is called a family of lines.

The equation of a straight line is given by,

\(y = mx + c\)

Here, the two important characteristics of a straight line are:

\(m ? \) slope of the line

\(c ?\,y-\)intercept

While the slope describes how much the line rises or falls, the \(y-\)intercept gives the point of intersection of the line and \(y-\)axis.

Hence, there are two types of families.

Types of Family of Lines

There are two types of family of lines based on their similar properties.

1. Family of lines that have the same slope
2. Family of lines that have the same \(y-\)intercept.

Before learning to write the general equation of a family of lines, let us learn to write the joint equation of lines.

What is the Joint Equation of a Pair of Lines?

Let the two lines be \({a_1}x + {b_1}y + {c_1} = 0\) and \({a_2}x + {b_2}y + {c_2} = 0.\)

Therefore, the joint equation is given by, 

\(\left( {{a_1}x + {b_1}y + {c_1}} \right)\left( {{a_2}x + {b_2}y + {c_2}} \right) = 0\)

Or \(a{x^2} + 2hxy + b{y^2} + 2gx + 2fy + c = 0\)

Here, 

\(a = {a_1}{a_2}\)

\(b = {b_1}{b_2}\)

\(2h = {a_1}{b_2} + {a_2}{b_1}\)

\(2g = {a_1}{c_2} + {a_2}{c_1}\)

\(2f = {b_1}{c_2} + {b_2}{c_1}\)

\(c = {c_1}{c_2}\)

Thus, we can say that the joint equation of a pair of straight lines is also the general equation in the second degree.

A homogenous equation of the second degree represents a pair of straight lines passing through the origin as, 

\(a{x^2} + 2hxy + b{y^2} = 0\)

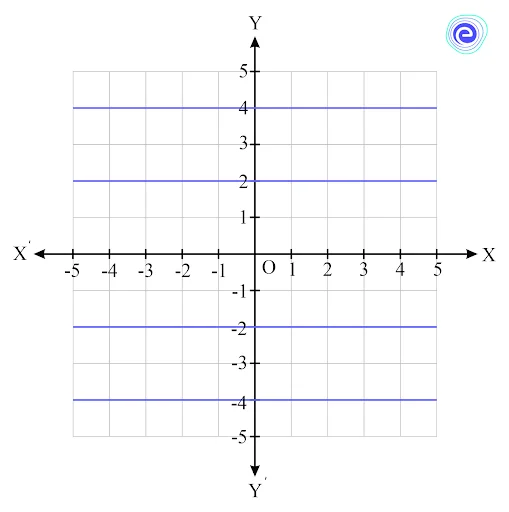
Family of Lines with the Same Slope

This family can be represented as shown below.

Observe that all these lines have the same slope. That is, they are parallel to each other. Although the lines look the same, they have different \(y-\)intercepts. Notice that the \(y-\)intercepts of these lines are shifting along the \(y-\)axis.

For smaller values of \(y-\)intercepts, the lines have smaller values of \(b.\) As the line rises on the vertical axis, the value of \(b\) increases too. This phenomenon is called the vertical shift.

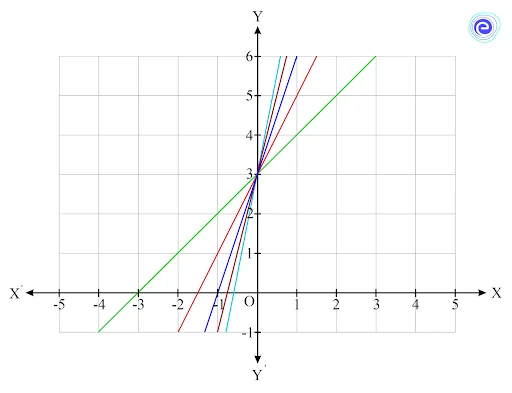
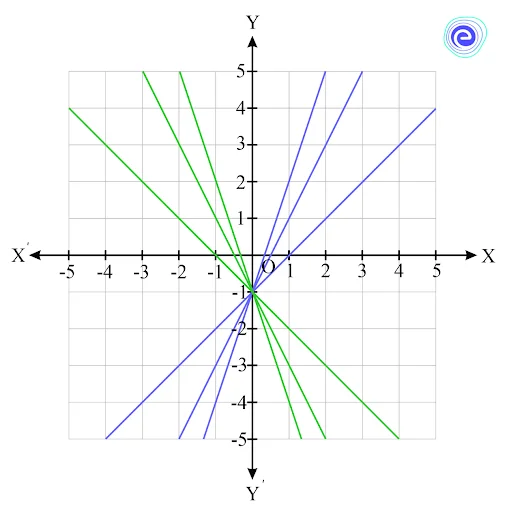
Family of Lines with the Same y-intercept

This family can be as shown below.

Observe that all these lines intersect at \((0,3).\) These and infinitely many more lines that can be drawn through a particular point is called family of lines. When three or more lines intersect at a point, they are also called concurrent lines. Hence, this is also a family of concurrent lines.

Equation of Family of Lines

Let \({a_1}x + {b_1}y + {c_1} = 0\) and \({a_2}x + {b_2}y + {c_2} = 0\) be two straight lines.

Then, \({a_1}x + {b_1}y + {c_1} + \lambda \left( {{a_2}x + {b_2}y + {c_2}} \right) = 0\) for \(k \ne 0\) 

Here, let’s say \(\left( {{x_1},{y_1}} \right)\) is the point of intersection of these lines. Then,

\({a_1}{x_1} + {b_1}{y_1} + {c_1} = 0\)

\({a_2}{x_1} + {b_2}{y_1} + {c_2} = 0\)

\( \Rightarrow {a_1}{x_1} + {b_1}{y_1} + {c_1} + \lambda \left( {{a_2}{x_1} + {b_2}{y_1} + {c_2}} \right) = 0\)

\(\therefore \lambda = 0\)

Thus, \(\left( {{x_1},{y_1}} \right)\) lies on \({a_1}x + {b_1}y + {c_1} + \lambda \left( {{a_2}x + {b_2}y + {c_2}} \right) = 0,\) for all values of \(\lambda\).

This can also be written as \({L_1} + \lambda {L_2} = 0,\) where \({L_1} = 0\) and \({L_2} = 0\) are the equations of two straight lines.

This means that the lines represented by various values of pass through the point of intersection.

Using Parallel and Perpendicular Lines

Follow these steps to find the equation of the family of lines when a parallel or perpendicular line and a passing through point are given.

Step 1: Write the given equation in the form \(y = mx + c.\)

Step 2: Find the slope of the given parallel or perpendicular line, say \({m_1}\)

Step 3: Using the slope from step 2, use one of the following conditions to find the slope of the required line, say \({m_2}\)

• For parallel lines: \({m_1} = {m_2}\)
• For perpendicular lines: \({m_1}{m_2} = – 1\)

Step 4: Use this value of \({m_2}\) and a given point, and write the equation of the required line in slope-intercept or point-slope form.

Solved Examples – Family of Lines

Q.1. Write the equations of the family of lines that satisfy the following conditions.
a. Parallel to \(x-\)axis
b. Perpendicular to the line \(2x+7y-9=0\)
c. Parallel to the line \(x+4y-12=0\)
d. Through \(\left( {0, – 1} \right)\)
Ans:
a. Parallel to \(x-\)axis
Equation of \(x-\)axis: \(y=0\)
This means that the slope of the \(x-\)axis is \(0.\)
Hence, the slope of all the lines parallel to the \(x-\)axis is also zero, but the \(y-\)intercept can be any number.

Therefore, the equation of the family of lines parallel to \(x-\)axis is given by,
\(y=c\)

b. Perpendicular to the line \(2x+7y-9=0\)
Rearrange of the form \(y=mx+c,\)
\(7y=9-2x\)
\(y = – \frac{{2x}}{7} + \frac{9}{7}\)
Here, \(m = – \frac{2}{7}\)
For perpendicular lines, \({m_1}{m_2} = – 1\)
Here, \({m_1} = – \frac{2}{7}\)
Therefore, slope of the family of lines perpendicular, \({m_2} = – \frac{2}{7}\)

Required equation of family of lines is \(y = \frac{7}{2}x + c.\)

c. Parallel to the line \(x+4y-12=0\)
Writing in slope-intercept form, \(y = – \frac{x}{4} + 3\)
Here, \(m = – \frac{1}{4}.\)

Since the slope of parallel lines are equal, the required equation of the family of lines is
\(y = – \frac{1}{4} + c\)

d. Through \(\left( {0, – 1} \right)\)
When a family of lines pass through \((0,-1),\) the \(y-\)intercept is \(-1.\)

Equation of lines passing through \((0,-1)\) is given by,
\(y=mx-1\)

Q.2. Find the equation of the family of lines parallel to \(x+y=0\) and passes through the point of intersection of the lines:
\(3x+y-1=0\)
\(x-y+5=0\)
Ans:
Given: Parallel line: \(x+y=0\)
Intersecting lines:
\(3x+y-1=0\)
\(x-y+5=0\)
Solving these intersecting lines, we get,
\(x=-1\)
\(y=4\)
\(∴\) The point of intersection is \(\left( { – 1,4} \right)\)
Any line parallel to \(x+y=0,\) is given by,
\(x+y=c\)
Since the line passes through \(\left( { – 1,4} \right),\)
\(-1+4=c\)
\(⇒c=3\)
Equation of the required family of lines is \(x+y=3\) or \(x+y-3=0\)

Q.3. A line through the point of intersection of the lines \(\frac{x}{a} + \frac{y}{b} = 1\) and \(\frac{x}{b} + \frac{y}{a} = 1\) meets the coordinate axes in \(A\) and \(B.\) Show that the locus of the midpoint of \(AB\) is the curve \(2xy(a + b) = ab(x + y).\)
Ans:
Let \((h,k)\) be the midpoint of the variable \(AB.\)
Equation of the line \(AB\) is
\((bx + ay – ab) + \lambda (ax + by – ab) = 0\)
Coordinates of \(A:(ab(1 + \lambda )b + \lambda a)\)
Coordinates of \(B:(0,{\rm{ab}}(1 + \lambda ){\rm{b}} + \lambda {\rm{a}})\)
\(∴\) Mid-point of \(AB = ({\rm{ab}}(1 + \lambda )2(\;{\rm{b}} + \lambda {\rm{a}})\)
\( \Rightarrow h = {\rm{ab}}(1 + \lambda )2(\;{\rm{b}} + \lambda {\rm{a}})\)
\(k = {\rm{ab}}(1 + \lambda )2({\rm{a}} + \lambda {\rm{b}})\)
\( \Rightarrow \frac{1}{{2\;h}} = b + \frac{{\lambda {\rm{a}}}}{{{\rm{ab}}(1 + \lambda )}}\)
\(\frac{1}{2}k = a + \frac{{\lambda b}}{{ab(1 + \lambda )}}\)
\( \Rightarrow \frac{1}{2}\;h + \frac{1}{2}k = a + \frac{b}{{ab}}\)
\(\therefore (h + k)ab = 2hk(a + b)\)
Therefore, the locus of the midpoint of \(AB\) is given by
\((x + y)ab = 2xy(a + b)\)
If \(a\) is the angle which this line makes with the given line and \(m\) is the slope of the required line, then 
\(\tan a = \frac{{{m_1} – m}}{{1 + {m_1}m}}\)

Note: 

• The above expression for tan⁡, gives two values of \(m,\) say \({m_A}\) and \({m_B}.\)
• The required equations of the lines through the point \(\left( {x_1,\,y_1} \right)\) and making equal angles with the given line are \(y – {y_1} = {m_A}\left( {x – {x_1}} \right);y – {y_1} = {m_B}\left( {x – {x_1}} \right).\)

Q.4. Write the equation of the family of lines perpendicular to \(6x+2y=24.\)
Ans:
To find \({m_1}:\)
Given: \(6x+2y=24\)
\(⇒2y=24-6x\)
\(∴y=12-3x\)
Here, \({m_1} = – 3\) and \(c=12\)
To find \({m_2}:\)
Condition for perpendicular lines: \({m_1}{m_2} = – 1\)
\( \Rightarrow {m_2} = – \frac{1}{{{m_1}}}\)
\({m_2} = – \frac{1}{{ – 3}}\)
\(\therefore {m_2} = \frac{1}{3}\)
Equation of the required family of lines is \(y = \frac{1}{3}m + c\)

Q.5. Find the line equation that passes through the point of intersection of the lines \(2x-3y+5=0\) and \(3x-2y+5=0,\) passing through the origin.
Ans:
Equation of line passing through the point of intersection of two lines \({L_1} = 0\) and \({L_2} = 0\) is given by
\({L_1} + \lambda {L_2} = 0\)
Given: Intersecting lines: \(2x-3y+5=0\) and \(3x-2y+5=0\)
\(∴\) Required line will be of the form:
\((2x – 3y + 5) + \lambda (3x – 2y + 5) = 0………\left( i \right)\)
Given: Line also passes through the origin \(O(0,0)\)
\( \Rightarrow (2(0) – 3(0) + 5) + \lambda (3(0) – 2(0) + 5) = 0\)
\(5 + \lambda 5 = 0\)
\(5\lambda = – 5\)
\(\therefore \lambda = – 1\)
Substituting in \((i),\) we get,
\((2x – 3y + 5) + ( – 1)(3x – 2y + 5) = 0\)
\(2x – 3y + 5 – 3x + 2y – 5 = 0\)
\( – x – y = 0\)
Hence, the required equation is,
\(x + y = 0\)

Summary

The general equation of a line is \(y=mx+c,\) where \(m\) is the slope and \(c\) is the \(y-\)intercept. Two or more lines that have at least one common feature are called a family of lines. They either have a common slope or \(y-\)intercept. While two or more parallel lines have the same slope, the product of the slopes of two perpendicular lines is \(-1.\) The lines represented by various values of \(\lambda \) pass through the point of intersection of lines \({L_1} = 0\) and \({L_2} = 0\) is given by \({L_1} + \lambda {L_2} = 0.\) This means that the lines represented by various values of \(\lambda \) pass through the point of intersection.

Frequently Asked Questions (FAQs)

Q.1. How do you find a family of lines?
Ans: The equation of a line passing through the point of intersection of two lines, say \({L_1} = 0\) and \({L_2} = 0\) is given by,
\({L_1} + \lambda {L_2} = 0\)
Here, \(\lambda\) is the parameter.

Q.2. How you solve a family of lines?
Ans: Here is one of the ways to find the family of lines.
Step 1: Find the point of intersection of the given lines.
Step 2: Find the required equation using the two-point form

Q.3. How do you separate the family lines?
Ans: Follow the steps to separate the equations of lines from the given family.
Step 1: Check the existence of the lines.
Step 2: Divide both sides of the equation by \({x^2}.\)
Step 3: Simplify the equation.
Step 4: Substitute \(m = \frac{y}{x}.\)
Step 5: Find the roots of the resulting quadratic equation in \(m,\) say, \({m_1}\) and \({m_2}.\)
Step 6: The separate equations are given by \(y = {m_1}x\) and \(y = {m_2}x.\)

Q.4. What is a family of straight lines?
Ans: A set of two or more lines that have at least one common feature, such as the slope, or \(y-\)intercept is called the family of lines. For example, a family of intersecting lines is the set of an infinite number of lines that have a common point of intersection \(P(x,y).\) This family of lines are also said to be concurrent.

Q.5. What is the equation of the family of lines through the point \((0,-1)\)?
Ans: All lines that pass through \((0,-1)\) have a common \(y-\)intercept, \(c=-1.\) The family of lines is given by: \(y=mx-1.\)

Learn about Lines in Geometry

We hope this detailed article on the Family of Lines will make you familiar with the topic. If you have any inquiries, feel to post them in the comment box. Stay tuned to embibe.com for more information.