First Principle of Differentiation: Derivative as a Rate Measurer, Geometrical Interpretation of Derivative at a Point

First Principle of Differentiation: A derivative is the first of the two main tools of calculus (the second being the integral). It is the instantaneous rate of change of a function at a point in its domain. This is the same thing as the slope of the tangent line to the graph of the function at that point. It’s a crucial idea with a wide range of applications: in everyday life, the derivative can inform us how fast we are driving or assist us in predicting the stock market changes. In this article, we will learn to find the rate of change of one variable with respect to another variable using the First Principle of Differentiation.

First Principle of Differentiation

Suppose $f$ is a real valued function, the function defined by
$\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$

wherever the limit exists is defined to be the derivative of $f$ at $x$ and is denoted by $f^{\prime }(x)$.
This definition of derivative is called the first principle of differentiation.
$\therefore f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$

There are different notations for derivative of a function. Sometimes $f^{\prime }(x)$ is denoted by $\frac{d}{dx}(f(x))$ or if $y=f(x)$, it is denoted by $\frac{dy}{dx}$.

Further, derivative of $f$ at $x=a$ is denoted by,
${\frac{df}{dx}|}_{x=a}or{\left(\frac{df}{dx}\right)}_{x=a}$

Derivative as a Rate Measurer

Let $f(x)$ be a function of $x$ and let $y=f(x)$. Here, $x$ is the independent variable, and $y$ is the dependent variable on $x$.

Let $\mathrm{\Delta }x$ be a small change (positive or negative) in $x$ and let $\mathrm{\Delta }y$ be the corresponding change in $y=f(x)$. Then, as the value of $x$ changes from $x$ to $x+\mathrm{\Delta }x$ and the value of $f(x)$ changes from $f(x)$ to $f(x+\mathrm{\Delta }x)$. So, change in the value of $f$ is given by,
$f(x+\mathrm{\Delta }x)–f(x)$ or $\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)–f(x)\dots \dots (i)$

Thus, we observe that due to change $\mathrm{\Delta }x$ in $x$, there is a change $\mathrm{\Delta }y$ in $y$. Therefore, due to one unit change in $x$, the corresponding change in $y$ is $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$.

This is known as the average rate of change of $y$ with respect to $x$.
As $\mathrm{\Delta }x\to 0$, we observe that $\mathrm{\Delta }y\to 0$.

$\therefore$ Rate of change in $y$ with respect to $x=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$.
$=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x+\mathrm{\Delta }x)–f(x)}{\mathrm{\Delta }x}$     [Using $(i)$]
$=\frac{d}{dx}(f(x))$     [Using definition of first principleof differentiation]
$=\frac{dy}{dx}$

Thus, $\frac{dy}{dx}$ measures the rate of change of $y=f(x)$ with respect to $x$.
i.e., $\frac{dy}{dx}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x+\mathrm{\Delta }x)–f(x)}{\mathrm{\Delta }x}$

Conclusion:
We can say that the derivative of a function $y=f(x)$ is same as the rate of change of $f(x)$ with respect to $x$

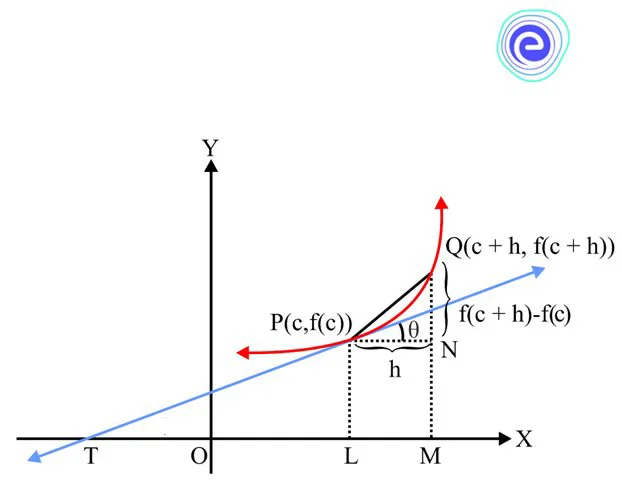
Geometrical Interpretation of Derivative at a Point

Let $f(x)$ be a differentiable function. Consider the curve $y=f(x)$.
Let $P(c,f(c))$ be a point on the curve $y=f(x)$ and let $Q(c+h,f(c+h))$ be a neighbouring point on the same curve. Then,
Slope of chord, $PQ=\tan \mathrm{\angle }QPN$
$=\frac{QN}{PN}$
$\therefore PQ=\frac{f(c+h)–f(c)}{h}$

Taking limit as $Q\to P$ i.e. $h\to 0$, we get,
$\underset{Q\to P}{lim}$( Slope of chord $PQ$) $=\underset{h\to 0}{lim}\frac{f(c+h)–f(c)}{h}\dots .(ii)$
As $Q\to P$, chord $PQ$ tends to the tangent to $y=f(x)$ at point $P$.
Therefore, from $(ii)$, we have
Slope of the tangent at $P=\underset{h\to 0}{lim}\frac{f(c+h)–f(c)}{h}$
$\Rightarrow$Slope of the tangent at $P=f^{\prime }(c)$ i.e., $\tan \theta =f^{\prime }(c)$, where $\theta$ is the inclination of the tangent to the curve $y=f(x)$ at point $(c,f(c))$ with the $x$−axis. 

Thus, the derivative of a function $f(x)$ at a point $x=c$ is the slope of the tangent to the curve $y=f(x)$ at the point $(c,f(c))$.

Derivative of Some Standard Functions From First Principles

1. Derivative of linear functions
   The derivative of a linear function is a constant, and is equal to the slope of the linear function.
   For Example: Let $f(x)=mx+b$
   This is an equation of the straight line with slope $m$ and $y$−intercept $b$.
   We can show using the first principle of derivative that $f^{\prime }(x)=m$
   Consider
   $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
   $\Rightarrow f^{\prime }(x)=\underset{h\to 0}{lim}\frac{m(x+h)+b–mx–b}{h}$
   $=\underset{h\to 0}{lim}\frac{mh}{h}$
   $=\underset{h\to 0}{lim}m$
   $=m$ [$\underset{h\to 0}{lim}c=c$, where $c$ is a constant].
   Hence, If $f(x)=mx+b$, then $f^{\prime }(x)=m$
   
2. Derivative of $f(x)=x^n$ is $n{x}^{n–1}$ for any positive integer $n$
   By definition of the derivative function, we have
   $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
   $=\underset{h\to 0}{lim}\frac{{(x+h)}^n–x^n}{h}$
   Using Binomial theorem,
   $(x+h{)}^n{=}^n{\mathrm{C}}_0{x}^n{+}^n{\mathrm{C}}_1{x}^{n–1}h+\dots {+}^n{\mathrm{C}}_n{h}^n$
   $(x+h{)}^n=x^n+n{x}^{n–1}h+\dots ..+h^n$
   Thus, $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{x^n+n{x}^{n–1}h+\dots +h–x^n}{h}$
   $\Rightarrow f^{\prime }(x)=\underset{h\to 0}{lim}\frac{n{x}^{n–1}h+\dots +h}{h}$
   $=\underset{h\to 0}{lim}\frac{h\left(n{x}^{n–1}+\dots +h^{n–1}\right)}{h}$
   $=\underset{h\to 0}{lim}\left(n{x}^{n–1}+\dots +h^{n–1}\right)$
   $=n{x}^{n–1}$ [On applying the limit]
   Hence, $\frac{d}{dx}\left(x^n\right)=n{x}^{n–1}$, for any positive integer $n$.
   
3. Derivative of $\sin x$ is $\cos x$.
   Let $f(x)=\sin x$
   $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
   $=\underset{h\to 0}{lim}\frac{\sin (x+h)–\sin (x)}{h}$
   $=\underset{h\to 0}{lim}\frac{2\cos \left(\frac{2x+h}{2}\right)\sin \left(\frac{h}{2}\right)}{h}\left[\sin A–\sin B=2\cos \left(\frac{A+B}{2}\right)\sin \left(\frac{A–B}{2}\right)\right]$
   $=\underset{h\to 0}{lim}\cos \left(x+\frac{h}{2}\right)\cdot \underset{h\to 0}{lim}\frac{\sin \frac{h}{2}}{\frac{h}{2}}$
   $=\cos x\cdot 1$
   $\therefore \frac{d}{dx}\sin x=\cos x$
   
4. Derivative of $\tan x$ is ${\sec }^{2}x$.
   Let $f(x)=\tan x$
   $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
   $=\underset{h\to 0}{lim}\frac{\tan (x+h)–\tan (x)}{h}$
   $=\underset{h\to 0}{lim}\frac{1}{h}\left[\frac{\sin (x+h)}{\cos (x+h)}–\frac{\sin x}{\cos x}\right]$
   $=\underset{h\to 0}{lim}\left[\frac{\sin (x+h)\cos x–\cos (x+h)\sin x}{h\cos (x+h)\cos x}\right]$
   $=\underset{h\to 0}{lim}\frac{\sin (x+h–x)}{h\cos (x+h)\cos x}$ [Using the formula for $\sin (A+B)$ ]
   $=\underset{h\to 0}{lim}\frac{\sin h}{h}\cdot \underset{h\to 0}{lim}\frac{1}{\cos (x+h)\cos x}$
   $=1\cdot \frac{1}{{\cos }^{2}x}$
   $\therefore \frac{d}{dx}(\tan x)={\sec }^{2}x$

Solved Examples

Q.1. Differentiate $\sqrt{2x+3}$ with respect to $x$ from the first principle.
Ans: Given: $f(x)=\sqrt{2x+3}$
$\Rightarrow f(x+h)=\sqrt{2(x+h)+3}$
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{\sqrt{2(x+h)+3}–\sqrt{2x+3}}{h}$
$=\underset{h\to 0}{lim}\frac{\left[\sqrt{2(x+h)+3}–\sqrt{2x+3}\right]\left[\sqrt{2(x+h)+3}+\sqrt{2x+3}\right]}{h\left[\sqrt{2(x+h)+3}+\sqrt{2x+3}\right]}$
$=\underset{h\to 0}{lim}\frac{(2x+2h+3–2x–3)}{h}\times \frac{1}{\left[\sqrt{2x+2h+3}+\sqrt{2x+3}\right]}$
$=\underset{h\to 0}{lim}\frac{2h}{h}\times \underset{h\to 0}{lim}\frac{1}{\left[\sqrt{2x+2h+3}+\sqrt{2x+3}\right]}$
$=2\times \frac{1}{\sqrt{2x+3}+\sqrt{2x+3}}$
$=\frac{2}{2(\sqrt{2x+3})}$
$\therefore \frac{d}{dx}(\sqrt{2x+3})=\frac{1}{\sqrt{2x+3}}$

Q.2. Differentiate $\sqrt{4–x}$ with respect to $x$ from first principle.
Ans: Given: $f(x)=\sqrt{4–x}$
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{\sqrt{4–(x+h)}–\sqrt{4–x}}{h}$
$=\underset{h\to 0}{lim}\frac{\left[\sqrt{4–(x+h)}–\sqrt{4–x}\right]\left[\sqrt{4–(x+h)}+\sqrt{4–x}\right]}{h\left[\sqrt{4–(x+h)}+\sqrt{4–x}\right]}$
$=\underset{h\to 0}{lim}\frac{4–(x+h)–(4–x)}{h\left[\sqrt{4–(x+h)}+\sqrt{4–x}\right]}$
$=\underset{h\to 0}{lim}\frac{–h}{h\left[\sqrt{4–x–h}+\sqrt{4–x}\right]}$
$\therefore \frac{d}{dx}(\sqrt{4–x})=\frac{–1}{2\sqrt{4–x}}$

Q.3. Differentiate ${\sin }^{2}x$ with respect to $x$ from first principle.
Ans: Given: $f(x)={\sin }^{2}x$
$\Rightarrow f(x+h)={\sin }^2(x+h)$
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{{\sin }^2(x+h)–{\sin }^{2}x}{h}$
$=\underset{h\to 0}{lim}\frac{\sin (x+h+x)\sin (x+h–x)}{h}\left[{\sin }^{2}A–{\sin }^{2}B=\sin (A+B)\sin (A–B)\right]$
$=\underset{h\to 0}{lim}\frac{\sinh }{h}\times \underset{h\to 0}{lim}[\sin (2x+h)]$
$=1(\sin 2x)$
$\therefore \frac{d}{dx}(x)=\sin 2x$

Q.4. Differentiate $x{e}^x$ from first principles.
Ans: Given: $f(x)=x{e}^x$
$\Rightarrow f(x+h)=(x+h)e^{(x+h)}$
From the definition of first principles, we have,
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{(x+h)e^{x+h}–x{e}^x}{h}$
$=\underset{h\to 0}{lim}\frac{\left(x{e}^{x+h}–x{e}^x\right)+h{e}^{x+h}}{h}$
$=\underset{h\to 0}{lim}\left\{x{e}^x\left(\frac{e^h–1}{h}\right)+e^{x+h}\right\}$
$=x{e}^x\underset{h\to 0}{lim}\left(\frac{e^h–1}{h}\right)+\underset{h\to 0}{lim}{e}^{x+h}$
$=x{e}^x+e^x\left[\underset{h\to 0}{lim}\left(\frac{e^h–1}{h}\right)=1\right]$
$\therefore \frac{d}{dx}\left(x{e}^x\right)=x{e}^x+e^x$
$\Rightarrow \frac{d}{dx}\left(x{e}^x\right)=e^x(x+1)$

Q.5. Differentiate $\cot \sqrt{x}$ from first principle.
Ans: Given: $f(x)=\cot \sqrt{x}$
$\Rightarrow f(x+h)=\cot \sqrt{x+h}$
From the definition of first principles, we have,
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{\cot \sqrt{x+h}–\cot \sqrt{x}}{h}$
$=\underset{h\to 0}{lim}\frac{\frac{\cos (\sqrt{x+h})}{\sin (\sqrt{x+h})}–\frac{\cos (\sqrt{x})}{\sin (\sqrt{x})}}{h}$
$=\underset{h\to 0}{lim}\frac{\sin (\sqrt{x})\cos (\sqrt{x+h})–\cos (\sqrt{x})\sin (\sqrt{x+h})}{h\sin (\sqrt{x+h})\sin (\sqrt{x})}$
$=\underset{h\to 0}{lim}\frac{–\sin (\sqrt{x+h}–\sqrt{x})}{h\sin \sqrt{x+h}\sin \sqrt{x}}$
$=\underset{h\to 0}{lim}\frac{–\sin (\sqrt{x+h}–\sqrt{x})}{\left[(x+h)–x\right]\sin \sqrt{x+h}\sin \sqrt{x}}$
$=–\underset{h\to 0}{lim}\frac{\sin (\sqrt{x+h}–\sqrt{x})}{(\sqrt{x+h}–\sqrt{x})(\sqrt{x+h}+\sqrt{x})\sin \sqrt{x+h}\sin \sqrt{x}}$
$=–\underset{h\to 0}{lim}\frac{\sin (\sqrt{x+h}–\sqrt{x})}{\sqrt{x+h}–\sqrt{x}}\times \underset{h\to 0}{lim}\frac{1}{(\sqrt{x+h}+\sqrt{x})\sin \sqrt{x+h}\sin \sqrt{x}}$
$=–\frac{1}{2\sqrt{x}\sin \sqrt{x}\sin \sqrt{x}}=\frac{–{\mathrm{cosec}}^2\sqrt{x}}{2\sqrt{x}}$
$\therefore \frac{d}{dx}(\cot \sqrt{x})=\frac{–{\mathrm{cosec}}^2\sqrt{x}}{2\sqrt{x}}$

Q.6. Differentiate $e^{\sqrt{\tan x}}$ from first principle.
Ans: Let $f(x)=e^{\sqrt{\tan x}}$
$f(x+h)=e^{\sqrt{\tan (x+h)}}$
From the first principle
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{e^{\sqrt{\tan \left(x+h\right)}}–e^{\sqrt{{}^{\tan x}}}}{h}$
$=\underset{h\to 0}{lim}{e}^{\sqrt{\tan x}}\left\{\frac{e^{\sqrt{\tan (x+h)}–\sqrt{\tan x}}–1}{h}\right\}$
$=e^{\sqrt{\tan x}}\underset{h\to 0}{lim}\left\{\frac{e^{\sqrt{\tan (x+h)}–\sqrt{\tan x}}–1}{\sqrt{\tan (x+h)}–\sqrt{\tan x}}\times \frac{\sqrt{\tan (x+h)}–\sqrt{\tan x}}{h}\right\}$
$=e^{\sqrt{\tan x}}\times 1\times \underset{h\to 0}{lim}\left(\frac{\sqrt{\tan (x+h)}–\sqrt{\tan x}}{h}\times \frac{\sqrt{\tan (x+h)}+\sqrt{\tan x}}{\sqrt{\tan (x+h)}+\sqrt{\tan x}}\right)\left[\underset{x\to 0}{\because lim}\frac{e^x–1}{x}=1\right]$
$=e^{\sqrt{\tan x}}\underset{h\to 0}{lim}\frac{\tan (x+h)–\tan x}{h}\times \frac{1}{\sqrt{\tan (x+h)}+\sqrt{\tan x}}$
$=e^{\sqrt{\tan x}}\underset{h\to 0}{lim}\left(\frac{\frac{\sin (x+h)}{\cos (x+h)}–\frac{\sin x}{\cos x}}{h}\times \frac{1}{\sqrt{\tan (x+h)}+\sqrt{\tan x}}\right)$
$=e^{\sqrt{\tan x}}\underset{h\to 0}{lim}\left(\frac{\sin (x+h)\cos x–\sin x\cos (x+h)}{h\cos (x+h)\cos x}\times \frac{1}{\sqrt{\tan (x+h)}+\sqrt{\tan x}}\right)$
$=e^{\sqrt{\tan x}}\underset{h\to 0}{lim}\left(\frac{\sin (x+h–x)}{h\cos (x+h)\cos x}\times \frac{1}{\sqrt{\tan (x+h)}+\sqrt{\tan x}}\right)$
$=e^{\sqrt{\tan x}}\underset{h\to 0}{lim}\left(\frac{\sin h}{h\cos (x+h)\cos x}\times \frac{1}{\sqrt{\tan (x+h)}+\sqrt{\tan x}}\right)$
$=e^{\sqrt{\tan x}}\left(1\times x\times \frac{1}{2\sqrt{\tan x}}\right)$
$=\frac{e^{\sqrt{\tan x}}}{2\sqrt{\tan x}}{\sec }^{2}x$
Hence, $\frac{d}{dx}\left(e^{\sqrt{\tan x}}\right)=\frac{e^{\sqrt{\tan x}}}{2\sqrt{\tan x}}{\sec }^{2}x$

Q.7. Differentiate $x{\tan }^{–1}x$ from first principle 
Ans: $f(x)=x{\tan }^{–1}x$, then $f(x+h)=(x+h){\tan }^{–1}(x+h)$
Using the first principle of differentiation,
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$
$=\underset{h\to 0}{lim}\frac{(x+h){\tan }^{–1}(x+h)–x{\tan }^{–1}x}{h}$
$=\underset{h\to 0}{lim}\left\{x\left\{\frac{{\tan }^{–1}(x+h)–{\tan }^{–1}x}{h}\right\}+\frac{h{\tan }^{–1}(x+h)}{h}\right\}$
$=\underset{h\to 0}{lim}\left\{\frac{x{\tan }^{–1}\left(\frac{x+h–x}{1+x(x+h)}\right)}{h}\right\}+\underset{h\to 0}{lim}{\tan }^{–1}(x+h)$
$\left[\because {\tan }^{–1}x–{\tan }^{–1}y={\tan }^{–1}\left(\frac{x–y}{1+xy}\right);xy>–1\right]$
$=x\underset{h\to 0}{lim}\left\{\frac{{\tan }^{–1}\left(\frac{h}{1+x(x+h)}\right)}{\frac{h}{1+x(x+h)}}\times \frac{1}{1+x(x+h)}\right\}+{\tan }^{–1}x$
$=\frac{x}{1+x^2}+{\tan }^{–1}x$
Hence, $\frac{d}{dx}\left(x{\tan }^{–1}x\right)=\frac{x}{1+x^2}+{\tan }^{–1}x$

Summary of First Principle of Differentiation

This article explains the first principle of differentiation which states that the derivative of a function $f(x)$ with respect to $x$ and it is given by $f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$. The derivative of a function $y=f(x)$ is same as the rate of change of $f(x)$ with respect to $x$. We also learnt that the derivative of a function $y=f(x)$ at a point is the slope of the tangent to the curve at that point. Further, some standard formulas of differentiation (or derivatives) of trigonometric and polynomial functions were derived using the first principle.

Frequently Asked Questions (FAQs)

Q.1. What is the first principle of differentiation?
Ans: The first principle rule of differentiation helps us evaluate the derivative of a function using limits. According to this rule, the derivative of the function $y=f(x)$ with respect to $x$ is given by:
$f^{\prime }(x)=\underset{h\to 0}{lim}\frac{f(x+h)–f(x)}{h}$

Q.2. What is $\frac{dy}{dx}$?
Ans: $\frac{dy}{dx}$ is an operation which indicates the differentiation of $y$ with respect to $x$.

Q.3. What are the three rules of differentiation?
Ans: The three rules of differentiation are
Constant rule: The constant rule states that the derivative of a constant is zero i.e. $\frac{d}{dx}(k)=0$, where $k$ is a constant.
Power rule: $\frac{d}{dx}\left(x^n\right)=n{x}^{n–1}$, where $n$ is any real number.
Sum and Difference Rule: If $f(x)=g(x)+h(x)$ then $f^{\prime }(x)=g^{\prime }(x)+h^{\prime }(x)$

Q.4. Does differentiation give gradient? 
Ans: The formula to find the differentiation of the function, $y=f(x)$ at any point $c$ on its curve is given by ${\frac{dy}{dx}|}_{x=c}$, which is also the formula to find the gradient of the curve the point $(c,f(c))$.
For Example: The slope of the curve $y=x^2–2x–3$ at the point $P(2,–3)$ is evaluated as follows:
$\frac{dy}{dx}=2x–2$
And, at $x=2$, we have
${\frac{dy}{dx}|}_{x=2}=2(2)–2=2$
Hence, the slope of the given curve at the given point is $2$.
Thus, the slope of a curve at a point is found using the first derivative.

Q.5. What is the derivative of $2x$?
Ans: Let $y=2x$
Then, $\frac{d}{dx}\left(2x\right)=2\frac{d}{dx}\left(x\right)=2,\left[\frac{d}{dx}\left(x^n\right)=n{x}^{n–1},n\in R\right]$
Hence, the derivative of $2x$ is $2$.

We hope that this detailed article on the First Principle of Differentiation was helpful. If you have any doubts, then do let us know about it in the comment section below. Our team will get try to solve your queries at the earliest.