Speed, Distance & Time Formula: Definition, Formulas, Examples

Speed, distance and time are closely interrelated to each other. It is important to understand the relationship shared between these three phenomenons to understand how to implement the formulas appropriately in different sums. There are different formulas that can be used to calculate any of them when the other two factors are defined. This article will discuss and cover all the formulas related to speed, distance, and time and learn how they are interdependent.

What is Speed?

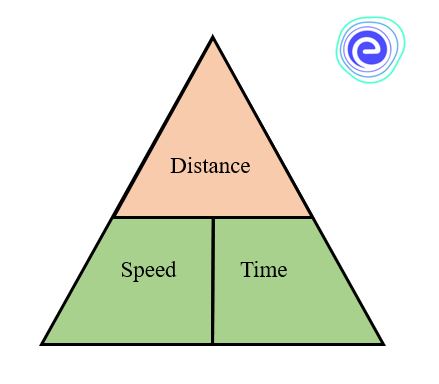
Speed is a measure of how quickly a body moves from one place to another place. The speed of a body is the distance covered by the body in unit time. Distance is the movement of an object in any particular direction. Time can be defined as the duration in which an object covers a given distance. It is possible to find the value of speed with the help of the other two terms. Let us look at the image below.

This image depicts the relationship between distance, speed and time.

\({\rm{Distance}} = {\rm{Speed}} \times {\rm{Time}}\)

\({\rm{Speed}} = \frac{{{\rm{Distance}}}}{{{\rm{Time}}}}\)

\({\rm{Time}} = \frac{{{\rm{Distance}}}}{{{\rm{Speed}}}}\)

To find speed, if:
1. Distance is in metre \(\left( {\rm{m}} \right)\) and time in seconds \(\left( {\rm{s}} \right)\), then the speed is in metre per second (\({\rm{m}}{{\rm{s}}^{ – 1}}\) or \({\rm{m}}/{\rm{s}}\)).
2. Distance is in kilometre \(\left( {{\rm{km}}} \right)\) and time in hours \(\left( {\rm{h}} \right)\) then the speed is in kilometre per hour (\({\rm{km}}{{\rm{h}}^{ – 1}}\) or \({\rm{km}}/{\rm{h}}\))

To find the distance, if:

1. Speed is in \(\left( {{\rm{m}}{{\rm{s}}^{ – 1}}} \right)\), time must be in second.
2. Speed is in \(\left( {{\rm{km}}{{\rm{h}}^{ – 1}}} \right)\), time must be in hour.

To find time, if:

1. Speed is in \(\left( {{\rm{m}}{{\rm{s}}^{ – 1}}} \right)\), the distance must be in metre \(\left( {\rm{m}} \right)\).
2. Speed is in \(\left( {{\rm{km}}{{\rm{h}}^{ – 1}}} \right)\) the distance must be in kilometre \(\left( {\rm{km}} \right)\).

Let us solve a couple of examples to understand the concept better.

Example 1: Priya covers a distance of \(1.2\,{\rm{km}}\) in \(40\) minutes. Find her speed in a) \(\left( {{\rm{km}}{{\rm{h}}^{{\rm{ – 1}}}}} \right)\)    b) \(\left( {{\rm{m}}{{\rm{s}}^{{\rm{ – 1}}}}} \right)\).

Solution: a) To get speed in kilometres per hour, the distance covered must be in kilometres, and the time taken must be in hours.
The given distance is \({\rm{1}}{\rm{.2}}\,{\rm{km}}\) and time \({\rm{ = }}\,{\rm{40}}\,{\rm{minutes}}\,{\rm{ = }}\frac{{40}}{{60}}{\rm{hour}} = \frac{2}{3}{\rm{hour}}\)
Therefore, \({\rm{speed}} = \frac{{{\rm{Distance}}}}{{{\rm{Time}}}} = \frac{{1.2}}{{\frac{2}{3}}} = 1.2 \times \frac{3}{2}{\rm{km}}{{\rm{h}}^{ – 1}} = 1.8\,{\rm{km}}{{\rm{h}}^{ – 1}}\)
b) To get speed in meters per second, the distance covered must be in metres, and the time taken must be in seconds.
The given distance is \(1.2\,{\rm{km}} = 1.2 \times 1000\,{\rm{m}} = 1200\,{\rm{m}}\), and \({\rm{time}} = 40\,{\rm{minutes}} = 40 \times 60 = 2400\,{\rm{seconds}}\)
Therefore, \({\rm{speed}} = \frac{{{\rm{Distance}}}}{{{\rm{Time}}}} = \frac{{1200}}{{2400}} = \frac{1}{2}{\rm{m}}{{\rm{s}}^{ – 1}}\)

Uniform Speed, Variable Speed and Average Speed

If an object covers equal distances in equal intervals of time, its speed is said to be uniform; otherwise, its speed is known as variable speed. For example,

1. If the car covers \(80\,{\rm{km}}\) in the first hour, \(80\,{\rm{km}}\) in the second hour, \(80\,{\rm{km}}\) in the third hour, and so on, its speed is uniform.
2. If a car covers \(55\,{\rm{km}}\) in the first hour, \(65\,{\rm{km}}\) in the second hour, \(45\,{\rm{km}}\) in the third hour, and so on, its speed is variable.
3. And, if a car covers the first \(70\,{\rm{km}}\) in the first hour, \(60\,{\rm{km}}\) in \(1\) hour \(30\) minutes, \(55\,{\rm{km}}\) in \(55\) hour \(10\) minutes, and so on, its speed is also variable.
4. The average speed can be defined as the total distance covered by a body in a particular time interval. The average speed can be calculated by dividing the total distance travelled by the total time taken.
   Therefore, the average speed of an object \( = \frac{{{\rm{Total}}\,{\rm{distance}}\,{\rm{covered}}\,{\rm{by}}\,{\rm{it}}}}{{{\rm{Total}}\,{\rm{time}}\,{\rm{taken}}}}\)

Let us have a quick look at a couple of examples to understand the concept better.

Example 1: Manu runs \(200\) metres in \(25\) seconds. Find
a) His speed
b) The distance run by him in \(5\) seconds

Solution: a) \({\rm{Speed}} = \frac{{{\rm{Distance}}}}{{{\rm{Time}}}} = \frac{{200}}{{25}} = 8\,{\rm{m}}{{\rm{s}}^{ – 1}}\)
b) Distance run by him in \(5\) seconds \( = {\rm{Speed}} \times {\rm{Time}}\)
\( = 8\,{\rm{m}}{{\rm{s}}^{ – 1}} \times 5\)
\( = 40\,{\rm{metres}}\)

Example 2: A car covers \(120\,{\rm{km}}\) in \(2\) hours, next \(160\,{\rm{km}}\) in \(3\) hours and last \(140\,{\rm{km}}\) again in \(2\) hours. Find the average speed of the train.

Solution: Average speed of the car \( = \frac{{{\rm{Total}}\,{\rm{distance}}\,{\rm{covered}}\,{\rm{by}}\,{\rm{it}}}}{{{\rm{Total}}\,{\rm{time}}\,{\rm{taken}}}}\)
Since, total distance covered \( = 120\,{\rm{km}} + 160\,{\rm{km}} + 140\,{\rm{km}}\,{\rm{ = 420}}\,{\rm{km}}\)
Total total time \(2\,{\rm{hours}} + 3\,{\rm{hours}}\, + 2\,{\rm{hours}} = 7\,{\rm{hours}}\)
Thus, the average speed \( = \frac{{420}}{7} = 60\,{\rm{km}}{{\rm{h}}^{ – 1}}\).
Therefore, the average speed is \(60\,{\rm{km}}{{\rm{h}}^{ – 1}}\).

Converting Speed From One Unit to Another

To convert kilometre per hour \(\left( {{\rm{km}}{{\rm{h}}^{ – 1}}} \right)\) to meter per second \(\left( {{\rm{m}}{{\rm{s}}^{ – 1}}} \right)\) multiply the speed by \(\frac{5}{{18}}\). And, to convert meter per second \(\left( {{\rm{m}}{{\rm{s}}^{ – 1}}} \right)\) to kilometre per hour \(\left( {{\rm{km}}{{\rm{h}}^{ – 1}}} \right)\), multiply by \(\frac{{18}}{5}\).
Wondering how we landed in \(\frac{{5}}{18}\) and \(\frac{{18}}{5}\)????
Come, let us solve how we got \(\frac{5}{{18}}\)

\(1{\rm{km}}{{\rm{h}}^{ – 1}} = \frac{{1\,{\rm{kilometre}}}}{{1\,{\rm{hour}}}}\)
\( = \frac{{1000\,{\rm{metre}}}}{{60 \times 60\,{\rm{seconds}}}} = \frac{{1000}}{{3600}}{\rm{m}}{{\rm{s}}^{ – 1}}\)
\( = \frac{{10}}{{36}} = \frac{5}{{18}}{\rm{m}}{{\rm{s}}^{ – 1}}\)
And, similarly, we can deduce the other conversion as well.
Let us solve some examples based on the conversion from \({\rm{m}}{{\rm{s}}^{ – 1}}\) to \({\rm{km}}{{\rm{h}}^{ – 1}}\) and vice versa.

Example 1: Convert \({\rm{90}}\,{\rm{km}}{{\rm{h}}^{ – 1}}\) into \({\rm{m}}{{\rm{s}}^{ – 1}}\).

Solution: \({\rm{90}}\,{\rm{km}}{{\rm{h}}^{ – 1}}\)
\({\rm{90}}\,{\rm{km}}{{\rm{h}}^{ – 1}} = 90 \times \frac{5}{{18}}{\rm{m}}{{\rm{s}}^{ – 1}}\)
\( = 25\,{\rm{m}}{{\rm{s}}^{ – 1}}\)
Hence, \(90\,{\rm{km}}{{\rm{h}}^{ – 1}} = 25\,{\rm{m}}{{\rm{s}}^{ – 1}}\)

Example 2: Convert \(15\,{\rm{m}}{{\rm{s}}^{ – 1}}\) into \({\rm{km}}{{\rm{h}}^{ – 1}}\).

Solution: \(15\,{\rm{m}}{{\rm{s}}^{ – 1}}\)
\(15\,{\rm{m}}{{\rm{s}}^{ – 1}} = 15 \times \frac{{18}}{5}{\rm{km}}{{\rm{h}}^{ – 1}}\)
\( = 54\,{\rm{km}}{{\rm{h}}^{ – 1}}\)
Hence, \(15\,{\rm{m}}{{\rm{s}}^{ – 1}} = 54\,{\rm{km}}{{\rm{h}}^{ – 1}}\)

Solved Examples: Formulas Relating Speed, Time and Distance

Q.1. A boy covers first \(60\,{\rm{km}}\) of his journey at \(30\,{\rm{km}}{{\rm{h}}^{ – 1}}\) and remaining \(50\,{\rm{km}}\) at \(20\,{\rm{km}}{{\rm{h}}^{ – 1}}\).
a) Find Total time taken
b) His average speed during the whole journey
Ans: a) Time taken to cover first \(60\,{\rm{km}} = \frac{{60}}{{30}} = 2\,{\rm{hours}}\).
Time taken to cover the remaining \(50\,{\rm{km}} = \frac{{50}}{{20}} = \frac{5}{2}\,{\rm{hours}}\).
Therefore, the total time taken \( = 2 + \frac{5}{2}{\rm{hours}}\)
\( = \frac{9}{2}{\rm{hours}}\).
b) The total distance covered \( = 60\,{\rm{km}} + 50\,{\rm{km}} = 110\,{\rm{km}}\).
and the total time taken \( = \frac{9}{2}{\rm{hours}}\).
Therefore, the average speed of the boy \( = \frac{{{\rm{Total}}\,{\rm{distance}}\,{\rm{covered}}\,{\rm{by}}\,{\rm{the}}\,{\rm{boy}}}}{{{\rm{Total}}\,{\rm{time}}\,{\rm{taken}}}}\)
\( = \frac{{110}}{{\frac{9}{2}}}{\rm{km}}{{\rm{h}}^{ – 1}}\).
\( = \frac{{110 \times 2}}{9}{\rm{km}}{{\rm{h}}^{ – 1}} = \frac{{220}}{9}{\rm{km}}{{\rm{h}}^{ – 1}}\).
Hence, the average speed of the boy is \(\frac{{220}}{9}{\rm{km}}{{\rm{h}}^{ – 1}}\).

Q.2. A \(160\,{\rm{m}}\) long train is travelling at a speed of \(72\,{\rm{km}}{{\rm{h}}^{ – 1}}\), find the time taken by the train to pass,
a) the post               
b) a \(200\,{\rm{m}}\) long platform
Ans: a) Distance to be covered by the train \( = \) length of the train \( = 160\,{\rm{m}}\).
\({\rm{Speed}} = 72\,{\rm{km}}{{\rm{h}}^{ – 1}} = 72 \times \frac{5}{{18}}{\rm{m}}{{\rm{s}}^{ – 1}} = 20\,{\rm{m}}{{\rm{s}}^{ – 1}}\)
Thus, the time taken \( = \frac{{{\rm{Distance}}}}{{{\rm{Speed}}}} = \frac{{160}}{{20}} = 8\,{\rm{seconds}}\) seconds.
Hence, the train will take \(8\) seconds to cover the post.
b) Distance to be covered by the train \( = \) Length of the train \( + \) Length of the platform
\( = 160\,{\rm{m}} + 200\,{\rm{m}} = 360\,{\rm{m}}\)
Therefore, time taken to pass a \(200\,{\rm{m}}\) long post \( = \frac{{{\rm{Distance}}}}{{{\rm{Speed}}}} = \frac{{360}}{{20}}{\rm{seconds}}\)
\( = 18\,{\rm{seconds}}\).

Q.3. Priya and Preethu run with a speed of \(8\,{\rm{km}}{{\rm{h}}^{ – 1}}\) and \(11\,{\rm{km}}{{\rm{h}}^{ – 1}}\). They both start running from the same point, find the distance between them after \(2\) hours if they run in the
a) same direction
b) opposite directions
Ans: Distance run by Priya in \(2\,{\rm{hours}} = {\rm{Speed}} \times {\rm{Time}}\)
\(= 8\,{\rm{km}}{{\rm{h}}^{ – 1}} \times 2\,{\rm{hours}} = 16\,{\rm{km}}\)
Distance run by Preethu in \(2\,{\rm{hours}} = {\rm{Speed}} \times {\rm{Time}}\)
\(= 11\,{\rm{km}}{{\rm{h}}^{ – 1}} \times 2\,{\rm{hours}} = 22\,{\rm{km}}\)
a) Required distance when they are running in the same direction \( = \) Difference between the distances covered by Priya and Preethu
Thus, the required distance \(= 22\,{\rm{km}} – 16\,{\rm{km}} = 6\,{\rm{km}}\)
b) Required distance when they both are running in different directions \( = \) Sum of the distances covered by Priya and Preethu
Thus, the required distance \( = 22\,{\rm{km}} + 16\,{\rm{km}} = 38\,{\rm{km}}\)

Q.4. Convert \({\rm{75}}\,{\rm{cm}}{{\rm{s}}^{ – 1}}\) into \({\rm{km}}{{\rm{h}}^{{\rm{ – 1}}}}\)
Ans: \(75\,{\rm{cm}}{{\rm{s}}^{ – 1}} = 0.75\,{\rm{m}}{{\rm{s}}^{ – 1}}\).
\( = 0.75 \times \frac{{18}}{5}{\rm{km}}{{\rm{h}}^{ – 1}} = 2.7\,{\rm{km}}{{\rm{h}}^{ – 1}}\).

Q.5. Convert \(45\,{\rm{km}}{{\rm{h}}^{{\rm{ – 1}}}}\) into \({\rm{mmi}}{{\rm{n}}^{{\rm{ – 1}}}}\)
Ans: \(45\,{\rm{km}}{{\rm{h}}^{{\rm{ – 1}}}}\)
\(45\,{\rm{km}}{{\rm{h}}^{ – 1}} = \frac{{45\,{\rm{km}}}}{{1\,{\rm{hour}}}}\)
\( = \frac{{45 \times 1000}}{{60}}{\rm{mmi}}{{\rm{n}}^{{\rm{ – 1}}}}\)
\( = 750\,{\rm{mmi}}{{\rm{n}}^{{\rm{ – 1}}}}\).

Summary

In this article, we learnt about the correlation between distance, speed and time, and then we learnt that to find the value of any one quantity, we need the help of the other two quantities. Later on, we learnt the formulas to find the distance or speed or time. In addition to this, we learnt about the average speed, and we solved a couple of examples to learn it better. We also learnt about the conversion of metres per second to kilometres per hour and vice versa.

Learn All the Concepts on Distance

Frequently Asked Questions (FAQs)

Frequently asked questions related to speed, distance and time is listed as follows:

Q.1. What is the relationship between speed, distance and time formula?
Ans: Speed is a measure of how quickly a body moves from one place to another place, or the speed of a body is the distance covered by the body in unit time. Distance is the amount of movement of an object in any particular direction. Time can be defined as the duration in which an object covers a given distance.
Therefore, we can say that distance is directly proportional to speed and time. Speed is inversely proportional to time.

Q.2. How do you find distance with speed and time questions?
Ans: Apply the formula, \({\rm{distance}} = {\rm{speed}} \times {\rm{time}}\), to calculate the distance.

Q.3. How do you calculate speed distance and time quickly?
Ans: With the help of the below-given formulas, we can quickly calculate the speed, distance, and time.
\({\rm{Speed}} = \frac{{{\rm{Distance}}}}{{{\rm{Time}}}}\)
\({\rm{Distance}} = {\rm{Speed}} \times {\rm{Time}}\),
\({\rm{Time}} = \frac{{{\rm{Distance}}}}{{{\rm{Speed}}}}\)

Q.4. What is the relation between distance and time?
Ans: Distance and time are inversely proportional to each other. If one quantity increases, the other decreases and vice versa.

Q.5. How does distance affect speed?
Ans: The speed is directly proportional to the distance travelled as,
\({\rm{Distance}} = {\rm{Speed}} \times {\rm{Time}}\)

We hope this detailed article on formulas relating to speed, time, and distance helped you in your studies. If you have any doubts, queries or suggestions regarding this article, feel to ask us in the comment section and we will be more than happy to assist you. Happy learning!