Frustum of a Pyramid: Definition, Properties, Volume

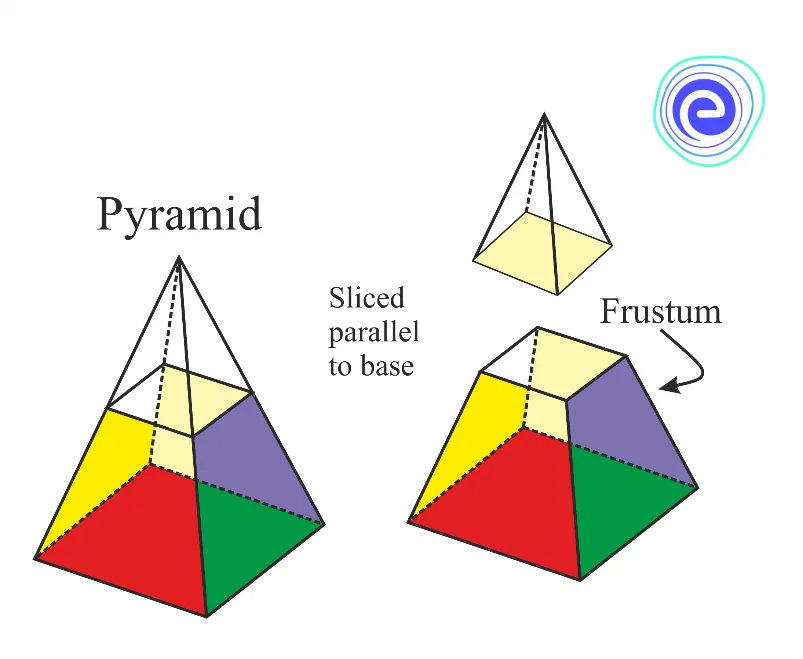
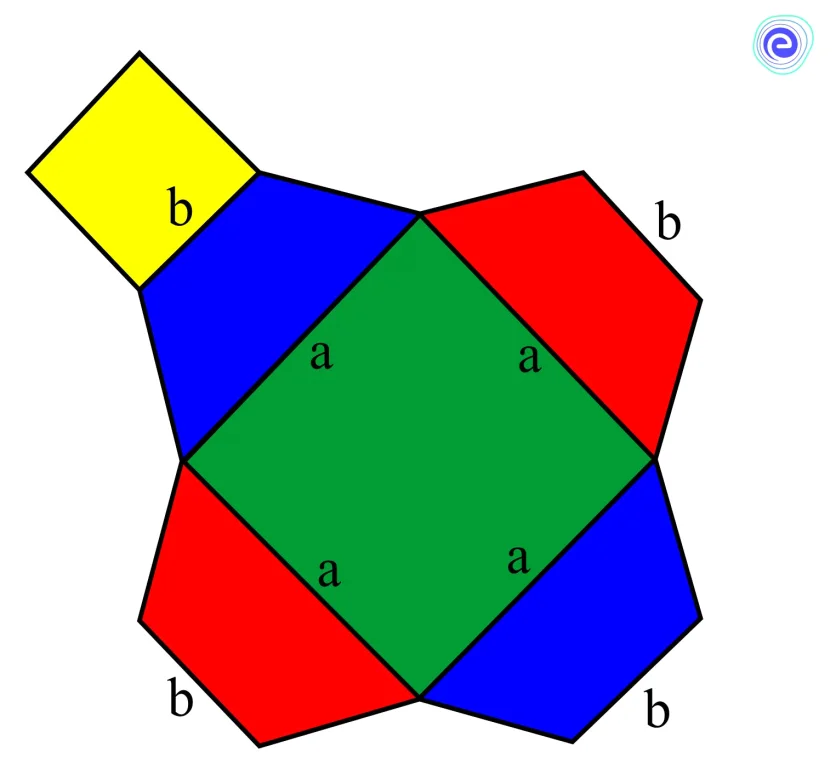
Frustum of a Pyramid: The frustum is a Latin word that means “cut off a piece”. A frustum is a 3-dimensional object created by cutting the pyramid’s apex. It has many properties that set it apart from other solid shapes. A frustum’s top and bottom bases are parallel. Each face of a pyramid is an isosceles trapezoid.

The area of each side face can be calculated using the area of the trapezoid formula given by the half of the product of the height and the sum of parallel sides. The frustum of a pyramid is used to view the lenses in computer graphics. In the engineering study, in aerospace, a frustum of a pyramid is also used.

Frustum of a Pyramid Definition

The frustum is a pyramid formed by slicing the top off of a conventional pyramid. That is why it is referred to as a truncated pyramid. The section of a pyramid between the vertex and the base that is cut through by a plane parallel to its base is known as the frustum of the pyramid.

The various elements of a frustum of a pyramid are listed below:

• Upper Base – The base that is formed by removing the pyramid. It is the base of a frustum of a pyramid on the top side.
• Lower Base – The bottom base of the frustum of a pyramid or the original base of the pyramid.
• Altitude – Perpendicular distance between the bases of the frustum of a pyramid.
• Slant Height – Distance between the bases measured along the frustum’s lateral side.

Properties of Frustum of a Pyramid

The following are the properties of a frustum of a pyramid:

• A frustum of a pyramid has the two polygonal bases such as square, triangle etc.
• The lateral surfaces of a frustum of a pyramid are in trapezium shape.
• The axis of a frustum is almost always the pyramid’s axis (the original shape).
• A frustum is a right frustum if the axis is perpendicular to the base; otherwise, it is an oblique frustum. 

Types of Frustums

There are two common types of frustums of pyramids:

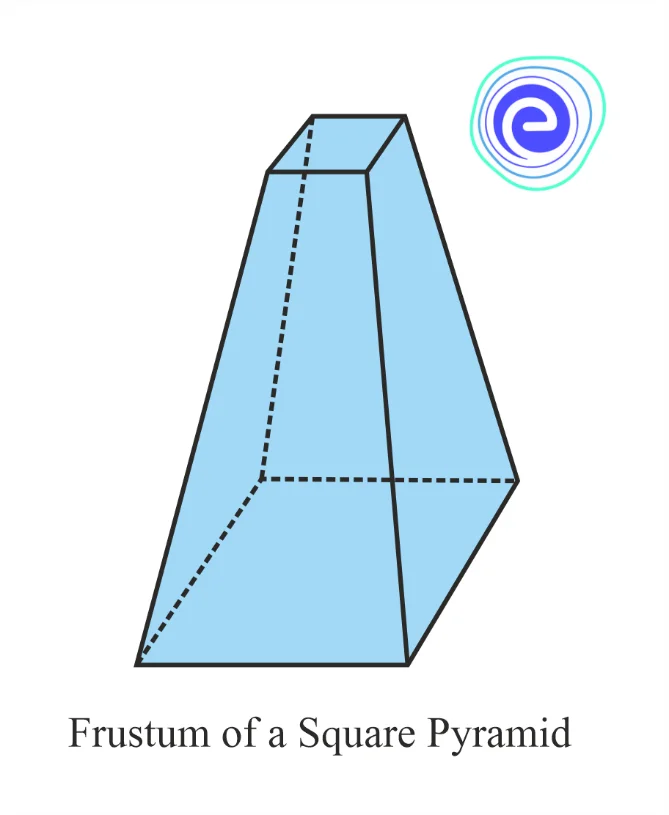
• Frustum of a Square Pyramid

This is a frustum of a pyramid whose bases are in the shape of a square.

• Frustum of a Triangular Pyramid

This is a frustum of a pyramid whose bases are shaped like a triangle.

Lateral Surface Area of Frustum of a Pyramid

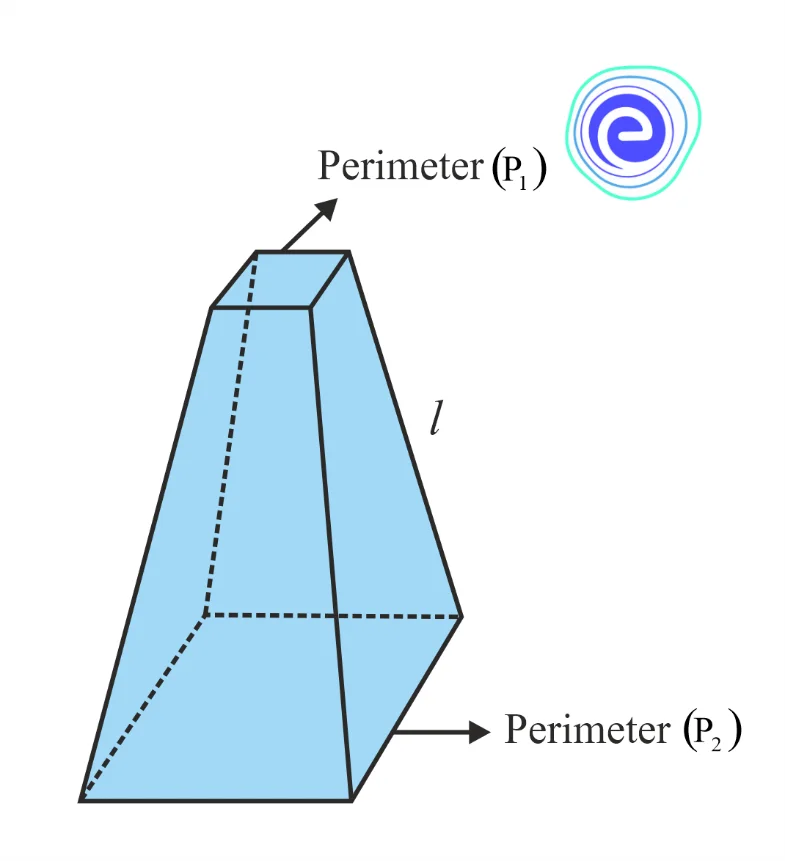
The perimeters of the bases and the slant height can be used to calculate the lateral surface area of any frustum. The formula for calculating the lateral (or curved) surface area of the frustum of a pyramid is given by

The lateral surface area, \(\mathrm{LSA}=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times l\)

• \(P_{1}\) – Perimeter of one base of the frustum of a pyramid
• \(P_{2}\) – Perimeter of another base of the frustum of a pyramid
• \(l\) – Slant height of the frustum of a pyramid

Derivation of LSA Formula

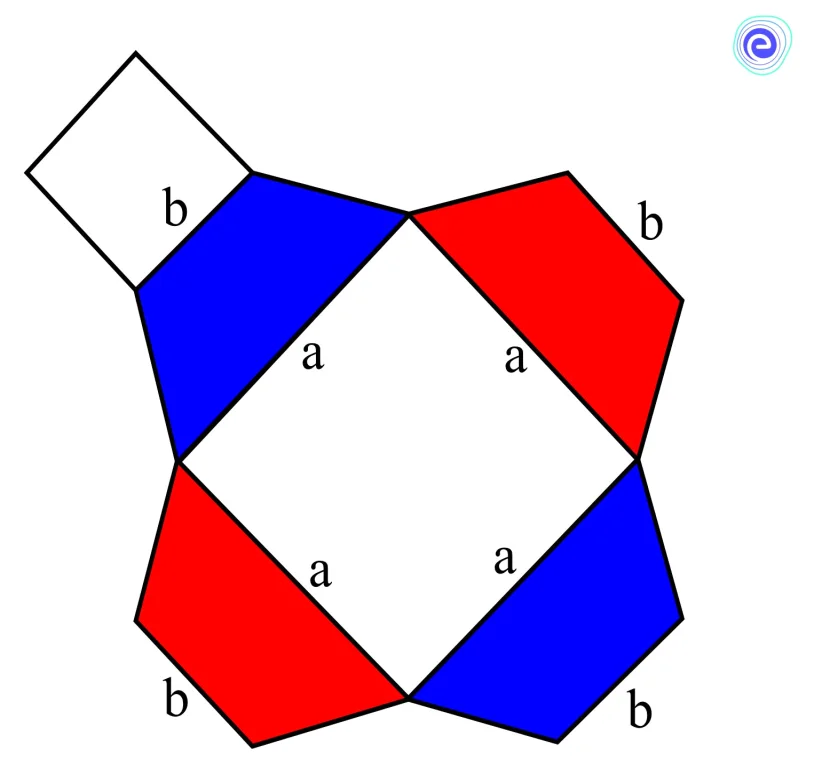
Let us consider the base length of the bigger square is \(a\) units and the length of the smaller square is \(b\) units.

We know that the lateral surface area of the frustum of a pyramid is the sum of areas of four surfaces (trapeziums).

\(\mathrm{LSA}=\) sum of areas of four sides

\(\mathrm{LSA}=4 \times\) Area of trapezium

We know that area of the trapezium \(=\frac{1}{2} \times(\) sum of the parallel sides \() \times(\) height \()\)

So, \(\mathrm{LSA}=4 \times \frac{1}{2}(a+b) \times l\)

\(\mathrm{LSA}=\frac{1}{2}(4 a+4 b) \times l\)

We know that the perimeter of a square is \(4 \times\) side.

So, L.S.A \(=\frac{1}{2} \times(\) Perimeter of base \(1\) (bigger square) \(+\) perimeter of base \(2(\) smaller square) \(\times l\)

\(L . S . A=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times L\)

Total Surface Area of Frustum of a Pyramid

The total surface area of the frustum of a pyramid is equal to the sum of the lateral surface area and the area of bases of the frustum.

Total Surface Area \((TSA)=\) Lateral surface area of a frustum of a pyramid \(+\) area of the bases of a frustum of a pyramid.

Derivation of TSA Formula

Let us consider the base length of a bigger square is \(a\) units and the length of a smaller square is \(b\) units.

We know that the total surface area of the frustum of a pyramid is the sum of areas of four surfaces (trapeziums) and the areas of bases.

\(\mathrm{TSA}=\) Sum of areas of six sides

\(\mathrm{TSA}=4 \times\) Area of trapezium \(+\) area of base \(1+\) area of base \(2\)

\(\mathrm{TSA}=4 \times \frac{1}{2}(a+b) \times l+S_{1}+S_{2}\)

\(\mathrm{TSA}=\frac{1}{2}(4 a+4 b) \times l+S_{1}+S_{2}\)

\(\mathrm{TSA}=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times l+S_{1}+S_{2}\)

\(\therefore\) Total surface area, \(\mathrm{TSA}={L S A}+S_{1}+S_{2}\)

Where,

• \(P_{1}-\) The perimeter of one base of the frustum of a pyramid
• \(P_{2}-\) The perimeter of another base of the frustum of a pyramid
• \(L-\) Slant height of the frustum of a pyramid
• \(S_{1}-\) Area of the base \(1\)
• \(S_{2}-\) Area of the base \(2\)

Note: As each side face of a pyramid is an isosceles trapezoid, the area of each side face can be calculated using the area of the trapezoid formula:

\(\frac{1}{2} \times(\) sum of the parallel sides \() \times(\) height \()\)

Frustum of a Pyramid Volume

Like every other \(3\)-dimensional shape, the volume of the frustum of a pyramid can be calculated using its height and base area.

\(V=\frac{1}{3} \times H \times\left(S_{1}+S_{2}+\sqrt{S_{1} S_{2}}\right)\)

Derivation of Volume Formula

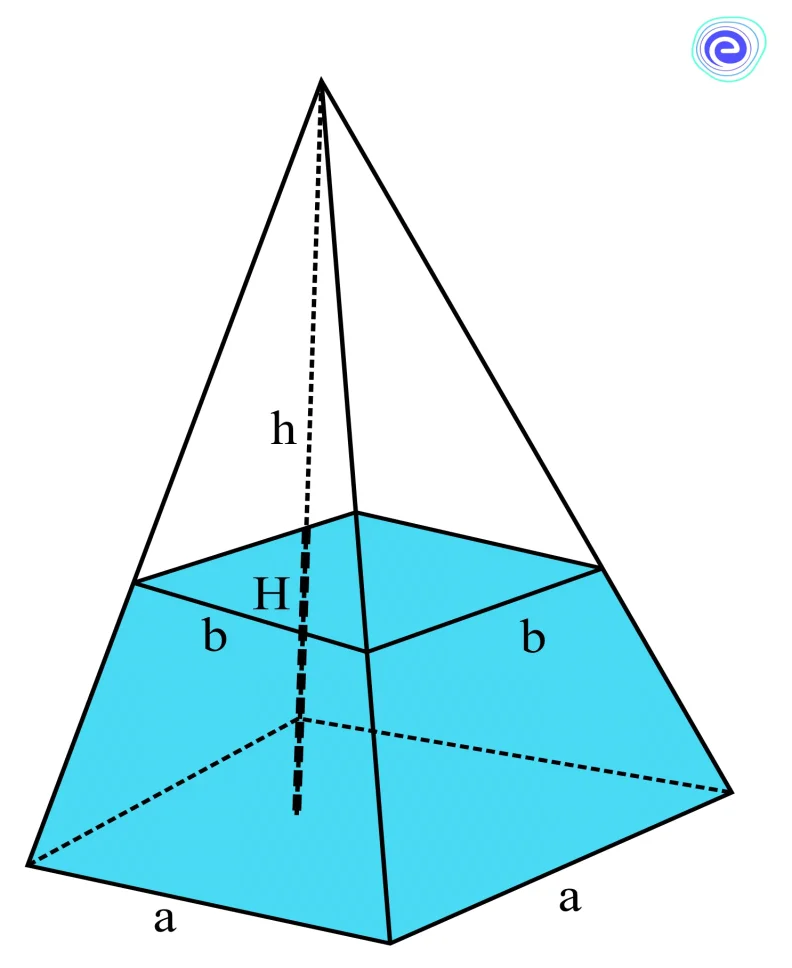
Consider a pyramid of base length \(a\) and height \(h\). The frustum of a pyramid of height \(H\) is formed by cutting the base (whose length is \(b\)).

We know that volume of the pyramid \(=\frac{1}{2} \times\) area of base \(\times\) height \(=\frac{1}{2} \times S_{1} \times h\)——–\((i)\)

Volume of the small pyramid formed after cutting is given \(=\frac{1}{3} \times S_{2} \times(h-H)\)——–\((ii)\)

Volume of the frustum of a pyramid \(=\) Volume of the whole pyramid \(-\) Volume of the small pyramid

\(=\frac{1}{3} \times S_{1} \times h-\frac{1}{2} \times S_{2} \times(h-H)\)

\(=\frac{1}{3} \times S_{1} \times h-\frac{1}{2} \times S_{2} \times h+\frac{1}{2} \times S_{2} \times H\)

\(=\frac{1}{3} \times h \times\left(S_{1}-S_{2}\right)+\frac{1}{2} \times S_{2} \times H……..(1)\)

For similar solids,

\(\frac{S_2}{S_1}=\frac{h-H}{H}\)

\(\sqrt{\frac{S_2}{S_1}}=1-\frac{H}{h}\)

\(\frac{H}{h}=1-\sqrt{\frac{S_{2}}{S_1}}\)

\(\frac{H}{h}=1-\frac{\sqrt{S_{2}}}{\sqrt{S_{1}}}\)

\(\frac{H}{h}=\frac{\sqrt{S_{1}}-\sqrt{S_{2}}}{\sqrt{S_{1}}}\)

\(\frac{h}{H}=\frac{\sqrt{S_{1}}}{\sqrt{S_{1}}-\sqrt{S_{2}}}\)

\(h=H \times \frac{\sqrt{S_{1}}}{\sqrt{S_{1}}-\sqrt{S_{2}}}\)

\(h=H \times \frac{\sqrt{S_{1}}}{\sqrt{S_{1}}-\sqrt{S_{2}}} \times \frac{\sqrt{S_{1}}+\sqrt{S_{2}}}{\sqrt{S_{1}}+\sqrt{S_{2}}}\)

\(h=H \times \frac{S_{1}+\sqrt{S_{2}} S_{1}}{S_{1}-S_{2}}\)

Substituting this value in equation \((1)\),

\(=\frac{1}{3} \times H \times \frac{S_{1}+\sqrt{S_{2}} S_{1}}{S_{1}-S_{2}} \times\left(S_{1}-S_{2}\right)+\frac{1}{2} \times S_{2} \times H\)

\(=\frac{1}{3} \times H \times\left(S_{1}+S_{2}+\sqrt{S_{1} S_{2}}\right)\)

\(V=\frac{1}{3} \times H \times\left(S_{1}+S_{2}+\sqrt{S_{1} S_{2}}\right)\)

Here,

• \(S_{1}\) – Area of one base of a frustum of a pyramid
• \(S_{2}\) – Area of another base of a frustum of a pyramid
• \(H\) – Height of the frustum of a pyramid (The distance between the centres of two bases of a frustum of a pyramid)

Solved Examples – Frustum of a Pyramid

Below are a few solved examples that can help in getting a better idea.

Q.1. The bases of a square pyramid’s frustum are \(10\) and \(7\) units long. It has a height of \(12\) units. Determine the volume.

Ans: Given: Height, \(H=12\) units

Bases, \(a_{1}=10\) units, \(a_{2}=7\) units.

\(\therefore\) Area of the base \(1\) is \(10^{2}=100\) square units

Area of the base \(2\) is \(7^{2}=49\) square units.

Volume of the frustum of a pyramid is \(V=\frac{1}{3} \times H \times\left(S_{1}+S_{2}+\sqrt{S_{1} S_{2}}\right)\)

\(V=\frac{1}{3} \times 12 \times(100+49+\sqrt{100 \times 49)}\)

\(V=4 \times(149+70)\)

\(\therefore V=876\) cubic units

Q.2. The bases of a square pyramid’s frustum are \(10\) and \(7\) units long. It has a slant height of \(12\) units. Determine the total surface area of the pyramid’s frustum.

Ans: Given: Slant height, \(L=12\) units

Bases, \(a_{1}=10, a_{2}=7\) units.

Perimeter of base \(1, P_{1}=4(10)=40\) units

Area of base \(1\) is \(10^{2}=100\) square units

Perimeter of base \(2, P_{2}=4(7)=28\) units

Area of base \(2\) is \(7^{2}=49\) square units

Total surface area of the frustum of a pyramid, \(T S A=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times L+\) area of bases

\(T S A=\frac{1}{2} \times(40+28) \times 12+100+49\)

\(\therefore T S A=557\) square units

Q.3. Determine its volume, whose bases of a square pyramid’s frustum are \(12\) and \(8\) units long. It has a height of \(14\) units.

Ans: Given: Height, \(H=14\) units

Bases, \(a_{1}=12, a_{2}=8\) units.

Area of the base \(1\) is \(12^{2}=144\) square units

Area of the base \(2\) is \(8^{2}=64\) square units.

Volume of the frustum of a pyramid, \(V=\frac{1}{3} \times H\times\left(S_{1}+S_{2}+\sqrt{S_{1}S_{2}}\right)\)

\(V=\frac{1}{3} \times 14 \times(144+64+\sqrt{144 \times 64)}\)

\(V=\frac{14}{3} \times(208+96)\)

\(\therefore V=1418.6\) cubic units

Q.4. A monument is in the shape of a frustum of a pyramid, whose upper and lower plane faces are squares with sides of \(16\) and \(9\) metres, respectively. Determine the volume of the monument if its height is \(21\) metres.

Ans: Given: A monument is in the shape of frustum of a pyramid.

Height, \(H=21\) units

Bases are \(a_{1}=16, a_{2}=9\) units.

Area of the base \(1\) is \(16^{2}=256\) square units

Area of the base \(2\) is \(9^{2}=81\) square units.

Volume of the frustum of a pyramid is \(V=\frac{1}{3} \times H \times\left(S_{1}+S_{2}+\sqrt{S_{1} S_{2}}\right)\)

\(V=\frac{1}{3} \times 21 \times(256+81+\sqrt{256 \times 81)}\)

\(V=7 \times(337+144)\)

\(\therefore V=3367\) cubic units

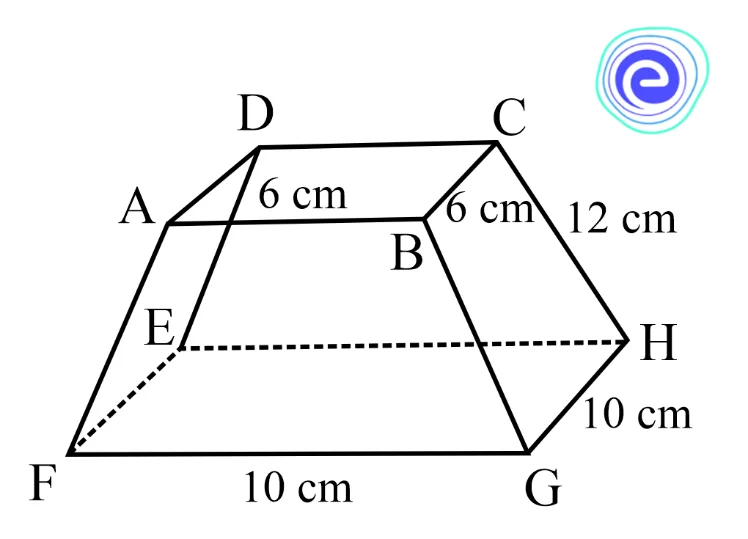
Q.5. The diagram below depicts a solid frustum of a pyramid with a \(6 \mathrm{~cm}\) square top and a \(10 \mathrm{~cm}\) square base. The frustum’s slant edge measures \(12 \mathrm{~cm}\). Find its lateral surface area.

Ans: Given: Slant edge of figure is \(12 \mathrm{~cm}\)

Bases are of length \(a_{1}=10 \mathrm{~cm}\) and \(a_{2}=6 \mathrm{~cm}\)

Perimeter of base \(1, P_{1}=4(10)=40 \mathrm{~cm}\)

Perimeter of base \(2, P_{2}=4(6)=24 \mathrm{~cm}\)

Lateral surface area of the frustum of a pyramid, \(L S A=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times L\)

\(=\frac{1}{2} \times 12 \times(40+24)\)

\(=6 \times 64\)

\(\therefore L S A=384 \mathrm{~cm}^{2}\)

Summary

The frustum of a pyramid is a solid figure formed by cutting plane parallel to base by removing the apex or vertex The top and bottom bases of the frustum of the pyramid are parallel to each other. The bases may be triangle or square.

The volume of the frustum of a pyramid is the amount of space in it and it is measured in cubic units. The lateral surface area of the frustum of a pyramid is the sum of areas of faces (trapezium). The total surface area of the frustum of a pyramid is the sum of lateral area and the areas of bases.

FAQs on Frustum of a Pyramid

Students might be having many questions with respect to the Frustum of a Pyramid. Here are a few commonly asked questions and answers:

Q.1. What is the formula for the lateral surface area of the frustum of a pyramid?
Ans: The lateral surface area of the frustum of a pyramid is given by
\(L S A=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times L\)
where \(P_{1}, P_{2}\) are the perimeter of bases, and \(L\) is the slant height.

Q.2. What is the total surface area of the frustum of a pyramid?
Ans: The total surface area of the frustum of a pyramid is the sum of lateral surface area and the area of bases of a frustum of a pyramid.

Q.3. How do you find the total surface area of a frustum of a square based pyramid?
Ans: The total surface area of the frustum of a square pyramid is
\(T S A=\frac{1}{2} \times\left(P_{1}+P_{2}\right) \times L+S_{1}+S_{2}\)
Where,
\(P_{1}-\) The perimeter of one base of the frustum of a pyramid
\(P_{2}-\) The perimeter of another base of the frustum of a pyramid
\(L-\) Slant height of the frustum of a pyramid
\(S_{1}-\) Area of the base \(1\)
\(S_{2}-\) Area of the base \(2\)

Q.4. What is the volume of a frustum of a pyramid?
Ans: The volume of a frustum of a pyramid is calculated by using the formula \(\frac{1}{3} \times H \times\left(S_{1}+S_{2}+\sqrt{S_{1} S_{2}}\right)\)
Where,
\(S_{1}-\) Area of one base of a frustum of a pyramid
\(S_{2}-\) Area of another base of a frustum of a pyramid
\(h\) height of the frustum of a pyramid

Q.5. What is a frustum of a pyramid?
Ans: If a right pyramid is cut by a plane parallel to the base, the portion of the pyramid between the plane and the base is known as the frustum of a pyramid.

Attempt 10th CBSE Exam Mock Tests

We hope this information about the Frustum of a Pyramid has been helpful. If you have any doubts, comment in the section below, and we will get back to you.

Stay tuned to embibe for the latest update on CBSE Exams.