Gay-Lussac’s Law: Introduction, Formula and Derivation

Gay-Lussac’s Law: Propane tanks are widely used for cooking purposes. However, it’s not fun to find out halfway through cooking that you’ve run out of gas. Gauges used to measure the pressure inside gas tanks register a higher pressure on a hot day than on a cold day. So, the air temperature needs to be considered when you decide whether or not to refill the tank before your next cook-out. In this article, we will learn about Gay Lussac’s Law, its formula and derivation in detail.

What is Gay-Lussac’s Law?

It was observed that on increasing the temperature of a gas sample in a closed container, the pressure of the gas sample increases as well. This is because an increase in temperature causes an increase in kinetic energy of the gas sample, which results in the gas molecules striking the walls of the container with greater force, hence greater pressure. 

The French chemist Joseph Gay-Lussac \((1778-1850)\) established the relationship between the pressure of a gas and its absolute temperature. 

Gay-Lussac’s Law states that at constant volume, the pressure of a given mass of gas varies directly with the gas’s absolute temperature. Gay-Lussac’s Law is very similar to Charles’s Law; the only difference is that in a Charles’s Law experiment, the container is flexible, whereas, in a Gay-Lussac’s Law experiment, the container is rigid.

The mathematical expressions for Gay-Lussac’s Law is:

\({\rm{P}} \propto {\rm{T}}\)

\(\frac{{\rm{P}}}{{\rm{T}}} = {\rm{k}}\)

Where:

1. \({\rm{P}}\) is the pressure exerted by the gas
2. \({\rm{T}}\) is the absolute temperature of the gas
3. \({\rm{k}}\) is a constant.

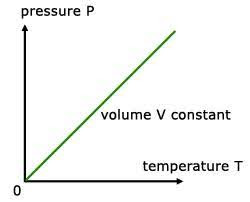
A graph of pressure vs. temperature also illustrates a direct relationship. Conversely, if a gas is cooled at a constant volume, its pressure continually decreases until the gas condenses to a liquid.

A graph of pressure versus temperature is a straight line extending up and away from the origin. The straight line indicates a directly proportional relationship.

Formula and Derivation

From Gay Lussac’s Law, we know that the pressure of a given mass of gas varies directly with the gas’s absolute temperature.

Mathematically,

\({\rm{P}} \propto {\rm{T}}\)

Hence, the initial temperature and pressure of a gas varies as:

\({{\rm{P}}_{\rm{1}}} \propto {{\rm{T}}_{\rm{1}}}\)

\(\frac{{{{\rm{P}}_{\rm{1}}}}}{{{{\rm{T}}_{\rm{1}}}}} = {\rm{k}}……..\)Eqn (1)

The final temperature and pressure of a gas varies as-

\({{\rm{P}}_{\rm{2}}} \propto {{\rm{T}}_{\rm{2}}}\)

\(\frac{{{{\rm{P}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}} = {\rm{k}}……..\)Eqn (2)

Combining Equation \((1)\) and Equation \((2),\) we get-

\(\frac{{{{\rm{P}}_{\rm{1}}}}}{{{{\rm{T}}_{\rm{1}}}}} = \frac{{{{\rm{P}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}}\)

\({{\rm{P}}_{\rm{1}}}{{\rm{T}}_{\rm{2}}} = {{\rm{P}}_{\rm{2}}}{{\rm{T}}_{\rm{1}}}\)

Where:

\({{\rm{P}}_{\rm{1}}}\) is the initial pressure
\({{\rm{T}}_{\rm{1}}}\) is the initial temperature
\({{\rm{P}}_{\rm{2}}}\) is the final pressure
\({{\rm{T}}_{\rm{2}}}\) is the final temperature

Hence, Gay-Lussac’s Law implies that for a gas of a fixed mass kept at a constant volume, the initial pressure and temperature ratio is equal to the ratio of the final pressure and temperature. Be sure to convert Fahrenheit and Celsius temperature to Kelvin when solving Gay-Lussac’s law problems.

Application of Gay-Lussac’s Law

1. Pressurized containers have warning labels stating that the container must be kept away from fire and stored in a cool environment. This is because when a pressurized aerosol can (such as a deodorant) is heated, the pressure exerted by the gases on the walls of the container increases(owing to Gay-Lussac’s Law) and can result in an explosion. 
2. The science behind pressure cookers is solely based on the relationship between temperature and pressure (Gay Lussac’s Law). When heat is applied externally to the pressure cooker, water inside it vaporizes to form steam. The steam contains enough heat energy for the food to be cooked.
3. A tyre blowout is a direct consequence of Gay Lussac’s Law. On a hot sunny day, as the temperature of the surrounding air rises, the pressure of the gas inside the tyre increases and exerts pressure on the walls of the tyre. Hence, after a certain threshold, the tyre bursts.
4. The physics of a bullet is principally based on Gay Lussac law. On pulling the trigger, a spring mechanism ignites the primer, which in turn ignites the propellant. The ignition of the propellant generates a lot of super-heated gas, which increases the pressure inside a bullet cartridge. As a result, a bullet is fired from a gun, leaving behind its cartridge.

Solved Example on Gay-Lussac’s Law

Q.1. An aerosol deodorant can have a pressure of \(3.00\;{\text{atm}}\) at \({25^ \circ }{\text{C}}.\) What is the pressure inside the can at a temperature of \({845^ \circ }{\text{C}}\)? This example illustrates why you shouldn’t incinerate aerosol cans.
Ans: \({{\rm{T}}_{\rm{1}}}{\rm{ = 25^\circ C = 298\,K}}\)
\({{\rm{T}}_{\rm{2}}}{\rm{ = 845^\circ C = 1118\,K}}\)
Next, plug the numbers into Gay-Lussac’s Law and solve for \({{\rm{P}}_{\rm{1}}}{{\rm{T}}_{\rm{2}}}{\rm{ = }}{{\rm{P}}_{\rm{2}}}{{\rm{T}}_{\rm{1}}}\)
\(\left( {{\rm{3}}{\rm{.00}}\,{\rm{atm}}} \right)\left( {{\rm{1118\,K}}} \right){\rm{ = }}\left( {{{\rm{P}}_{\rm{2}}}} \right)\left( {{\rm{298\,K}}} \right)\)
\({{\rm{P}}_{\rm{2}}}{\rm{ = }}\left( {{\rm{3}}{\rm{.00\,atm}}} \right)\left( {{\rm{1118\,K}}} \right){\rm{/}}\left( {{\rm{298\,K}}} \right)\)
\({P_2} = 11.3\,{\rm{atm}}\)

Q.2. Heating a gas cylinder to \({\text{250}}\,{\text{K}}\) raises its pressure to \({\text{2}}{\text{.0 atm}}{\text{.}}\) What was its initial temperature, assuming the gas started at ambient pressure \((1.0\;{\text{atm}})\)?
Ans: \({{\rm{P}}_{\rm{1}}}{{\rm{T}}_{\rm{2}}}{\rm{ = }}{{\rm{P}}_{\rm{2}}}{{\rm{T}}_{\rm{1}}}\)
\((1.0\;{\text{atm}})(250\;{\text{K}}) = (2.0\;{\text{atm}})({T_1})\)
\(\left( {{\rm{1}}{\rm{.0}}\,{\rm{atm}}} \right)\left( {{\rm{250}}\,{\rm{K}}} \right){\rm{ = }}\left( {{\rm{2}}{\rm{.0}}\,{\rm{atm}}} \right)\left( {{{\rm{T}}_{\rm{1}}}} \right)\)
\({{\rm{T}}_1} = 125\,{\rm{K}}\)
Note that doubling the absolute temperature of gas doubles its pressure. Similarly, halving the absolute temperature halves the pressure.

Q.3. Consider an ideal gas with an absolute temperature of \({{\rm{T}}_{\rm{1}}}\) To what absolute temperature would the gas need to be heated to double its pressure? Express the answer in terms of \({{\rm{T}}_{\rm{1}}}\)
Ans: \(\frac{{{{\rm{P}}_{\rm{1}}}}}{{{{\rm{T}}_{\rm{1}}}}} = \frac{{{{\rm{P}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}}\)
We want the pressure to double, so set \({{\rm{P}}_{\rm{1}}}{\rm{ = 1}}\) and \({{\rm{P}}_{\rm{2}}}{\rm{ = 2}}\) and temperature \({{\rm{T}}_{\rm{1}}}{\rm{ = 1}}\,{\rm{K}}\) and \({{\rm{T}}_{\rm{2}}}{\rm{ =  x}}\)
Therefore:
\(\frac{1}{1} = \frac{2}{{\rm{x}}}\)
\({\rm{x}} = {\rm{2K}}\)
Hence, \({{\rm{T}}_{\rm{2}}}\) would be double the value of \({{\rm{T}}_{\rm{1}}}\)

Q.4. A \({\text{30}}{\text{.0}}\,{\text{L}}\) sample of nitrogen inside a rigid, metal container at \({20.0^ \circ }{\text{C}}\) is placed inside an oven whose temperature is \({50.0^ \circ }{\text{C}}\) The pressure inside the container at \({20.0^ \circ }{\text{C}}\) was at \({\text{3}}{\text{.00}}\,{\text{atm}}{\text{.}}\) What is the pressure of the nitrogen after its temperature is increased to \({50.0^ \circ }{\text{C}}\)?
Ans: \(\frac{{{{\rm{P}}_{\rm{1}}}}}{{{{\rm{P}}_{\rm{2}}}}} = \frac{{{{\rm{P}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}}\)
\(\frac{{3.00}}{{293}} = \frac{{\rm{x}}}{{323}}\)
\({\rm{x}} = 3.31\,{\rm{atm}}\)

Summary

According to Gay Lussac’s Law, Pressure and temperature at constant volume are directly proportional to each other. On plotting the variables on a graph, a straight line is observed that moves away from the origin. Gay Lussac’s Law can be directly applied to our daily lives, such as using pressure cookers for cooking food, water heaters, etc. In this article, we learned the statement, formula, and derivation of Gay Lussac’s Law. We also learned how this Law is applicable in our day-to-day lives.

Frequently Asked Questions (FAQs) on Gay-Lussac’s Law

Q.1. What is Gay Lussac’s law formula?
Ans: Gay-Lussac’s Law states that the volume held constant, the pressure of a gas is directly proportional to its absolute temperature. Thus,
\(\frac{{\rm{P}}}{{\rm{T}}}{\rm{ = K}}\left( {{\rm{constant}}} \right)\)
Or,
\(\frac{{{{\rm{P}}_{\rm{1}}}}}{{{{\rm{T}}_{\rm{1}}}}} = \frac{{{{\rm{P}}_{\rm{2}}}}}{{{{\rm{T}}_{\rm{2}}}}}\)
\({{\rm{P}}_{\rm{1}}}{{\rm{T}}_{\rm{2}}} = {{\rm{P}}_{\rm{2}}}{{\rm{T}}_{\rm{1}}}\)
The above equations are the standard calculations for Gay-Lussac’s Law.

Q.2. What is the importance of Gay Lussac’s Law?
Ans: The importance of this gas law is that it illustrates the relationship between pressure and temperature of a gas sample when the volume is held constant. According to this Law, a rising gas’s temperature induces a relative increase in its pressure (assuming that the volume does not change). Similarly, reducing the temperature decreases the pressure exerted on the walls of the container.

Q.3. Explain the graph obtained in Gay Lussac’s formula.
A graph of pressure vs temperature illustrates Gay Lussac’s Law.

A graph of either pressure versus temperature is a straight line, extending up and away from the origin. The straight line indicates a directly proportional relationship.

Q.4. Explain any two applications of Gay Lussac’s Law.
Ans: 1. Cooking of food inside pressure cookers is solely based on Gay Lussac’s Law (the relationship between temperature and pressure). When we apply heat, water inside the pressure cooker vaporizes to form steam. The steam contains enough heat energy for the food to be cooked.
2. A tyre blowout is a direct consequence of Gay Lussac’s Law. On a hot sunny day, as the temperature of the surrounding air rises, the pressure of the gas inside the tyre increases and exerts pressure on the walls of the tyre. Hence, after a certain threshold, the tyre bursts.

Q.5. Why is it dangerous to dispose of an aerosol can by incineration?
It is dangerous to dispose of an aerosol can by incineration because heating a pressurized aerosol can (such as a deodorant) increases the pressure exerted by the gases on the walls of the container (owing to Gay-Lussac’s Law) and can result in an explosion.

Learn About Boyle’s Law Here

We hope this detailed article on Gay-Lussac’s Law will be helpful to you in your preparation. If you have any doubts please reach out to us through the comments section, and we will get back to you as soon as possible.