Inequalities Involving Absolute Values: Definition, Open-Closed Interval

Inequalities Involving Absolute Values: We are familiar with the equations in one variable and two variables. We also know how to solve statement problems by translating them into equations. It may not always be possible that we will be able to translate the word problems into equations.

We may get some statements involving signs of inequality, i.e. \(<\) (less than), \(>\) (greater than), \(\leq\) (less than or equal to), and \(\geq\) (grater than or equal to). Statements involving such signs are called inequations or inequalities. In linear programming problems, we use inequality to find the optimal solution.

What are Inequalities?

Suppose any statement expression, having some variable or variables, contains the sign less than \((<)\), greater than \((>)\), less than or equal to \((\leq)\), or greater than or equal \((\geq)\). In that case, such a statement is called an inequation or inequality.

Learn Everything About Absolute Values Here

Linear Inequation in One Variable

In this case, inequality must involve only one variable. For example, \(3 x-15 \geq 22\) involves one variable \(x\), while \(3 y<11\) involves one variable \(y\).

Replacement Set and Solution Set

The set from which the value of the variable \(x\) is chosen is called the replacement set, and its subset whose elements satisfy the given inequation is called its solution set.

Open and Closed Interval

In an open interval, endpoints are not included in the solution set. In a closed interval, endpoints are included in the solution set.

Open interval is denoted by () while closed interval by [ ]

• If \(a \leq x \leq b\), then it is denoted by \(x\) in \([a, b]\)
• If \(a<x<b\), then it is denoted by \(x\) in \((a, b)\)
• If \(a<x \leq b\), then it is denoted by \(x\) in \((a, b]\)
• If \(a \leq x<b\), then it is denoted by \(x\) in \([a, b)\)

If \(a\) and \(b\) are two real numbers such that \(a<b\), then the sets \((a, b]\) and \([a, b)\) are known as semi-open or semi-closed intervals.

Rules for Solving Linear Inequations

1. The sign of an inequation remains the same on adding or subtracting the same number or expression to each side.
2. The sign of inequality does not change when both sides of the inequality are multiplied or divided by the same positive quantity.
3. The sign of inequality is reversed when both sides of the inequality are multiplied or divided by the same negative quantity.

Steps to Solve Linear Inequations

In the case of a system of linear inequations in one variable:

• Step 1: Solve each inequation individually.
• Step 2: Write the solution sets of all the given linear inequations.
• Step 3: Find those values of \(x\) by taking the intersection or union of the solution sets, which satisfy all the linear Inequations simultaneously.

Absolute Value or Modulus of a Number

The absolute value or modulus of a real number \(x\) represents the quantity of \(x\). It is also known as the magnitude or absolute value of \(x\). Geometrically, it is represented as the distance of the number from zero on a real number line. Since the distance is always positive, the modulus or absolute value of a real number is represented as

\(\left| x \right| = \left\{ {\begin{array}{*{20}{c}} {x,}&{{\text{if}}}&{x > 0} \\ {0,}&{{\text{if}}}&{x = 0} \\ { – x,}&{{\text{if}}}&{x < 0} \end{array}} \right.\)

Examples: \(|4|=4\) and \(|-5|=-(-5)=5\)

We can say that if \(|x|=a\) means \(x=\pm a\).

Geometric Interpretation of Modulus

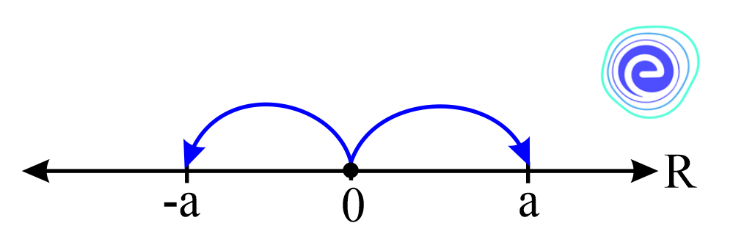
Absolute value is defined as the distance of a point from the origin. So, if \(|x|=a\) is given, that means the distance of a point on the number line from the origin is \(a\) units, and we know that there are two such points \(+a\) and \(-a\).

The difference between two real numbers \(x\) and \(a\) is denoted as \(|x-a|\) and represents the distance between \(x\) and \(a\) on the real number line.

\(\Rightarrow|x-a|=\) distance of \(x\) from \(a\).

If we consider \(a=0\), then \(|x|=\) distance of \(x\) from zero.

Inequalities Involving Absolute Values

An absolute value inequality is that which carries an absolute value symbol. It is a simple linear expression in one variable and has symbols like \(>,<, \geq\), and \(\leq\).

Properties of Modulus Involving Inequality

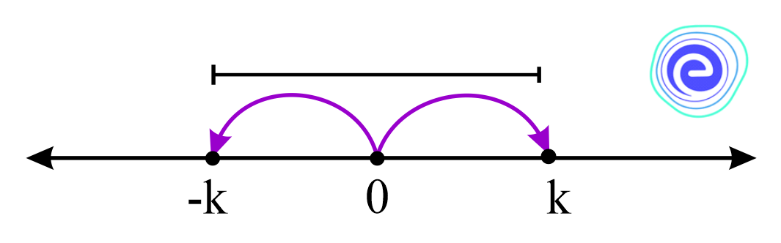
1. \(|x| \leq k\) where \(k\) is positive, since the absolute value of a number is always non-negative.

\(\Rightarrow\) Distance of \(x\) from zero is less than or equal to \(k\) unit.

\(\Rightarrow x \in[-k, k]\)

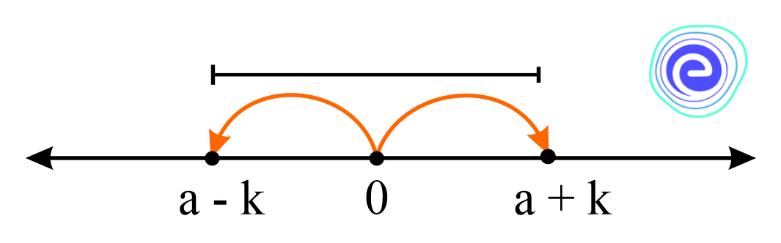
2. \(|x-a| \leq k\) where \(k\) is positive, since the absolute value of a number is always non-negative.

\(\Rightarrow\) Distance of \(x\) from \(a\) is less than or equal to \(k\) units.

\(\Rightarrow x \in[a-k, a+k]\)

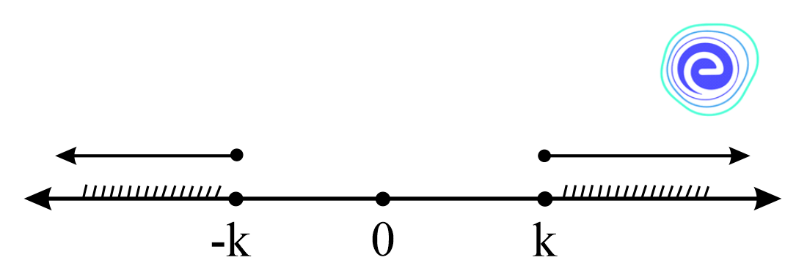
3. \(|x| \geq k\) where \(k\) is positive, since the absolute value of a number is always non-negative.

\(\Rightarrow\) Distance of \(x\) from zero is greater than or equal to \(k\) unit.

\(\Rightarrow x \leq-k\) or \(x \geq k\)

\(\Rightarrow x \in(-\infty,-k\rceil \cup[k, \infty)\)

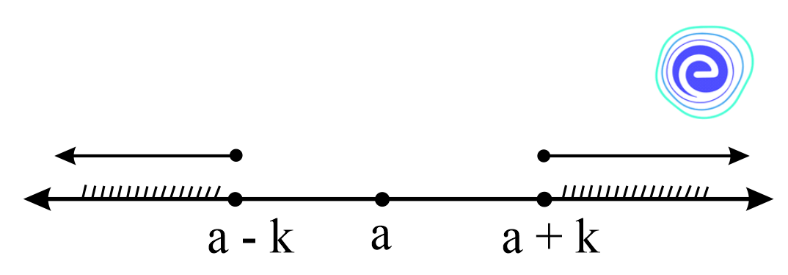
4. \(|x-a| \geq k\) where \(k\) is positive, since the absolute value of a number is always non-negative.

\(\Rightarrow\) Distance of \(x\) from \(a\) is greater than or equal to \(k\) unit.

\(\Rightarrow x \leq a-k\) or \(x \geq a+k\)

\(\Rightarrow x \in(-\infty, a-k] \cup[a+k, \infty)\)

5. \(|x|<k \Rightarrow x \in(-k, k)\)

6. \(|x-a|<k \Rightarrow x \in(a-k, a+k)\)

7. \(|x|>k \Rightarrow x<-k\) or \(x>k\)

\(\Rightarrow x \in(-\infty,-k) \cup(k, \infty)\)

8. \(|x-a|>k \Rightarrow x<a+k\) or \(x>a+k\)

\(\Rightarrow x \in(-\infty, a-k) \cup(a+k, \infty)\)

Exhaustive Method

To solve an absolute value inequality, equate quantities inside absolute value to zero and locate their roots on the real number line. These points help divide the real number line into intervals. Now, consider each interval as a separate case and solve the inequality in every case. Take the intersection of a solution set with case conditions.

For example, \(|x-2|+|x-3|<6\)

Here, \(x=2\) and \(3\) are critical points, so we will analyse the equation in following three cases.

Case I: If \(-\infty<x<2\), both \(x-2\) and \(x-3\) are negative numbers therefore \(|x-2|=2-x ;|x-3|=3-x\).

Substituting this in the original inequation, we get

\(2-x+3-x<6\)

\(\Rightarrow-2 x<1 \Rightarrow 2 x>-1 \Rightarrow x>-\frac{1}{2}\)

Now, by taking the intersection of the case condition and solution set, we get

\(x \in\left(-\frac{1}{2}, 2\right) \ldots\)…..(i)

Case II: If \(2 \leq x<3\), then \(x-2\) is non-negative, but \(x-3\) is a negative number. Therefore,

\(|x-2|=x-2 ;|x-3|=3-x\)

Substituting this in the original inequation, we get \(x-2+3-x<6 \Rightarrow 1<6\) which is true for all \(x\).

Now, by taking the intersection of the case condition and solution set, we get

\(x \in[2,3) \ldots\) …..(ii)

Case III: If \(x \geq 3\), both \(x-2\) and \(x-3\) are non-negative.

Therefore, \(|x-2|=x-2 ;|x-3|=x-3\)

Substituting this in the original inequation, we get \(x-2+x-3<6\)

\(\Rightarrow 2 x<11 \Rightarrow x<\frac{11}{2}\)

Now, by taking the intersection of the case condition and solution set, we get

\(x \in\left[3, \frac{11}{2}\right) \ldots\)…..(iii)

Lastly, taking the union of the solutions of the three cases, the final solution is obtained as

\(x \in\left(-\frac{1}{2}, \frac{11}{2}\right)\)

Solved Examples

Q.1. Solve the inequality \(|x|<7\), which involves the absolute value.
Sol:
The given equation is \(|x|<7\)
Case I: When \(x \geq 0\)
In this case \(|x|=x\), the given inequation becomes \(x<7\).
Thus, the solution is \(x \geq 0\) and \(x<7\) i.e., \(0 \leq x<7\) …..(i)
Case II: When \(x<0\)
In this case \(|x|=-x\), the given inequation becomes
\(-x<7\)
\(\Rightarrow x>-7\)
Thus, the solution is \(x<0\) and \(x>-7\)
\(\Rightarrow-7<x<0\) …..(ii)
Combining \((i)\) and \((ii)\), the required solutions of the given inequation are \(-7<x<7\). i.e., for all real numbers \(x\) is lying between \(-7\) and \(7\) .

Q.2. Solve \(|5 x-2| \leq \frac{3}{2}\).
Sol:
Let \(5 x-2=y\)
\(\therefore|5 x-2| \leq \frac{3}{2} \Rightarrow|y| \leq \frac{3}{2}\)
\(\Rightarrow-\frac{3}{2} \leq y \leq \frac{3}{2}\) \([\because|x| \leq a \Rightarrow-a \leq x \leq a]\)
\(\Rightarrow-\frac{3}{2} \leq 5 x-2 \leq \frac{3}{2}\)
\(\Rightarrow-\frac{3}{2}+2 \leq 5 x \leq \frac{3}{2}+2\)
\(\Rightarrow \frac{1}{2} \leq 5 x \leq \frac{7}{2}\)
\(\Rightarrow \frac{1}{10} \leq x \leq \frac{7}{10}\)
\(\therefore x \in\left[\frac{1}{10}, \frac{7}{10}\right]\)

Q3. Solve the following system of inequalities: \(|x-2| \leq 5,|x| \geq 2\).
Sol:
Given: \(|x-2| \leq 5\)
\(|x| \geq 2\)
Now,
\(|x-2| \leq 5 \Rightarrow\) Distance of \(x\) from \(2\) is less than or equal to \(5\) units.
\(\Rightarrow x \in[2-5,2+5]\) \([\because|x-a| \leq k \Rightarrow x \in[a-k, a+k]]\)
\(\Rightarrow x \in[-3,7]\) ……(i)
And \(\quad|x| \geq 2 \Rightarrow\) Distance of \(x\) from zero is greater than or equal to \(2\) units.
\(\Rightarrow x \leq-2\) or \(x \geq 2\)
\(\Rightarrow x \in(-\infty,-2] \cup[2, \infty)\)…….(ii)
Combining \((i)\) and \((ii)\), the required solutions to the given inequations are
\(x \in[-3,-2] \cup[2,7]\)

Q4. Solve the inequation \(|4 x-1|+2 \leq 10\) which involves the absolute value.
Sol:
Given: \(|4 x-1|+2 \leq 10\)
\(\Rightarrow|4 x-1|+2-2 \leq 10-2\)
\(\Rightarrow|4 x-1| \leq 8 \Rightarrow\) Distance of \(4x\) from \(1\) is less than or equal to \(8\) units.
\(\Rightarrow 4 x \in[1-8,1+8]\) \([\because|x-a| \leq k \Rightarrow x \in[a-k, a+k]]\)
\(\Rightarrow 4 x \in[-7,9]\)
\(\Rightarrow x \in\left[-\frac{7}{4}, \frac{9}{4}\right]\)

Q5. Solve \(\frac{|x|-2}{|x|-3} \geq 0, x \in R, x \neq \pm 3\)
Sol:
Given: \(\frac{|x|-2}{|x|-3} \geq 0, x \in R, x \neq \pm 3\)
For \(|x|\) there will be two case
Case I: For, \(x \geq 0,|x|=x\)
Then, \(\frac{x-2}{x-3} \geq 0\)
\(\therefore x \in[0,2] \cup(3, \infty) \quad \ldots(i)\)
\([As, x \neq \pm 3]\)
Case II: For, \(x<0,|x|=-x\)
Then, \(\frac{-x-2}{-x-3} \geq 0\)
\(\Rightarrow \frac{x+2}{x+3} \geq 0\)
\(\therefore x \in(-\infty,-3) \cup[-2,0)\ldots(ii)\)
\([As, x \neq \pm 3]\)
From \((i)\) and \((ii)\) we get
\(x \in(-\infty,-3) \cup[-2,2] \cup(3, \infty)\)

Summary

A statement with a sign of inequalities such as less than \((<)\), greater than \((>)\), less than or equal to \((\leq)\), or greater than or equal \((\geq)\), then such statement is called inequation or inequality. The endpoints are not included in the solution set in an open interval, but in a closed interval, the endpoints are included. Sign of inequality remains the same if both sides of the inequation are operated with the same number and magnitude. Geometrically, \(|x|=a\) is the distance of point \(x\) on a real number line from the origin is \(a\) units and \(|x-a|\) represents the distance between \(x\) and \(a\) on a real number line.

Frequently Asked Questions (FAQs)

Q.1. How do you solve inequalities with absolute value?
Ans: There are several steps to solve inequalities with absolute value. They are as follows:
(i) Step 1: Consider it as equality and solve it for the given variable.
(ii) Step 2: Plot the values of the variable on the number line and identify the interval on it.
(iii) Step 3: From each interval, take a random number and substitute it in the given inequality.
(iv) Step 4: The value satisfies the inequality, and the related interval of the value is the solution to the absolute value inequalities.

Q.2. What are the two parts of absolute value inequality?
Ans: Every absolute value inequality has two parts, which are separated by signs of inequality such as \(\leq, \geq,<\), or \(>\).

Q.3. What are the symbols used in absolute value inequality?
Ans: The symbols used in absolute value inequalities are greater than or equal to \((\geq)\), greater than \((>)\), less than or equal to \((\leq)\), and less than \((<)\).

Q.4. Where do we use absolute value inequalities?
Ans: The absolute value inequalities are used in many real-life situations and Mathematics. Sometimes it is not possible to translate every word problem into an equation. There are many questions in which we use absolute value inequalities.
Uses of absolute value inequality:
(i) To convert a word problem into an equation
(ii) To find the optimal solution to linear programming problems

Q.5. Can absolute values be fractions?
Ans: Yes, absolute values can be a fraction. If a fraction is positive, then it is its absolute value. If the fraction is negative, remove the negative sign to get the absolute value.
Example: The absolute value of \(\frac{2}{9}\) is \(\frac{2}{9}\), and the absolute value of \(-\frac{2}{9}\) is also \(\frac{2}{9}\).

We hope this detailed article on the Inequalities Involving Absolute Values will make you familiar with the topic. If you have any inquiries, feel to post them in the comment box. Stay tuned to embibe.com for more information.