- Written By
Keerthi Kulkarni
- Last Modified 27-12-2024
Introduction to Index Numbers: Introduction, Properties, Types, Formulas, Examples
Introduction to index numbers: An index number is a statistical instrument for assessing changes in the magnitude of a group of connected variables. It represents the overall trend of diverging ratios, used to calculate it. In most cases, index numbers are reported as a percentage.
Index numbers include the price index, the quantity index, and the value index. Index numbers are average subsets. A change in the level of an event is measured by an index number. The impact of changes over time is quantified by index numbers.
LEARN EXAM CONCEPTS ON EMBIBE
What are Index Numbers?
An index number is a relative measure used to compare and characterise the average change in price, quantity value, or other qualities of an item or a set of comparable goods through time, geographic location, or other factors.
- “An index number is a numerical value characterising the change in complex economic phenomena over a period of time or space,” according to Maslow.
- “An index number is a measure designed to illustrate changes in a variable on a collection of variables with respect to location, time or other features,” according to Spiegal.
- “Index numbers are instruments for measuring differences in the size of a group of related variables,” according to Croxton and Cowden.
- According to Bowley, “Index Numbers” are “a series that shows the motions of some quantity in its trend and fluctuations.”
Characterstics of Index Numbers
Index numbers are subsets of averages. They measure the change in the level of an event. Index numbers quantify the impact of changes over time.
- It is a type of average that is used to measure relative changes when absolute measurements are not possible.
- The index number only represents the preliminary changes in factors that may not be directly measured. It provides an overview of the relative changes.
- The method of calculating index numbers varies from variable to variable.
- It aids in comparing the levels of a phenomenon on a specific date to those on a previous date.
- It represents a special case of averages, specifically a weighted average.
- Index numbers are useful in all situations. The index used to determine price changes can also be used to determine industrial and agricultural production.
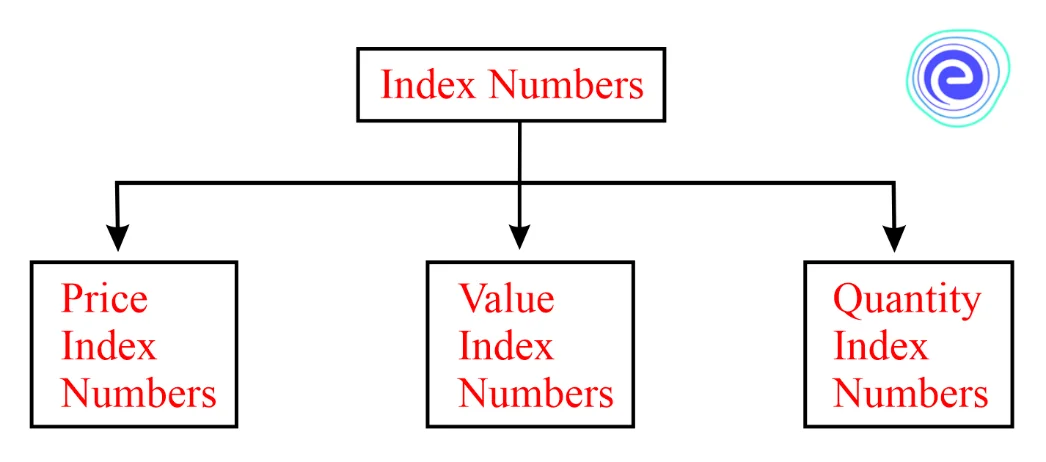
Types of Index Numbers
There are various types of index numbers, which are shown below.
1. Value Index Number
The value index number compares the current year’s price of a commodity to the previous year’s price. A commodity’s value is nothing more than the sum of the commodity’s price and its quantity. As a result, the value index number is equal to the sum of the current year’s commodity value divided by the total of the base year’s commodity value.
The formula for calculating the value index numbers is given by
\({V_{01}} = \frac{{\sum {{p_1}} q_1}}{{\sum {{p_0}} {q_0}}} \times 100\)
Here,
- \({V_{01}}\)-Value index of the present year based on the base year performance.
- \(\sum {{p_1}} {q_1}\)-Total values of the number of items consumed in the present year.
- \(\sum {{p_0}} {q_0}\) Total values of the number of items consumed in the base year.
We do not apply any weights to a value index number in this situation. Since these are regarded to be inherent in a commodity’s value, the value index number is an aggregate of values.
The value index number is a statistical device that is not often used. Price and quantity index figures provide a clearer picture of the economy for research and analysis. They also assist in the development and implementation of economic policies.
PRACTICE EXAM QUESTIONS AT EMBIBE
2. Quantity Index Numbers:
The change in the quantity or volume of items sold, consumed, or produced over a certain time period is measured by quantity index numbers. As a result, it measures relative changes in the quantity of a certain set of products across time.
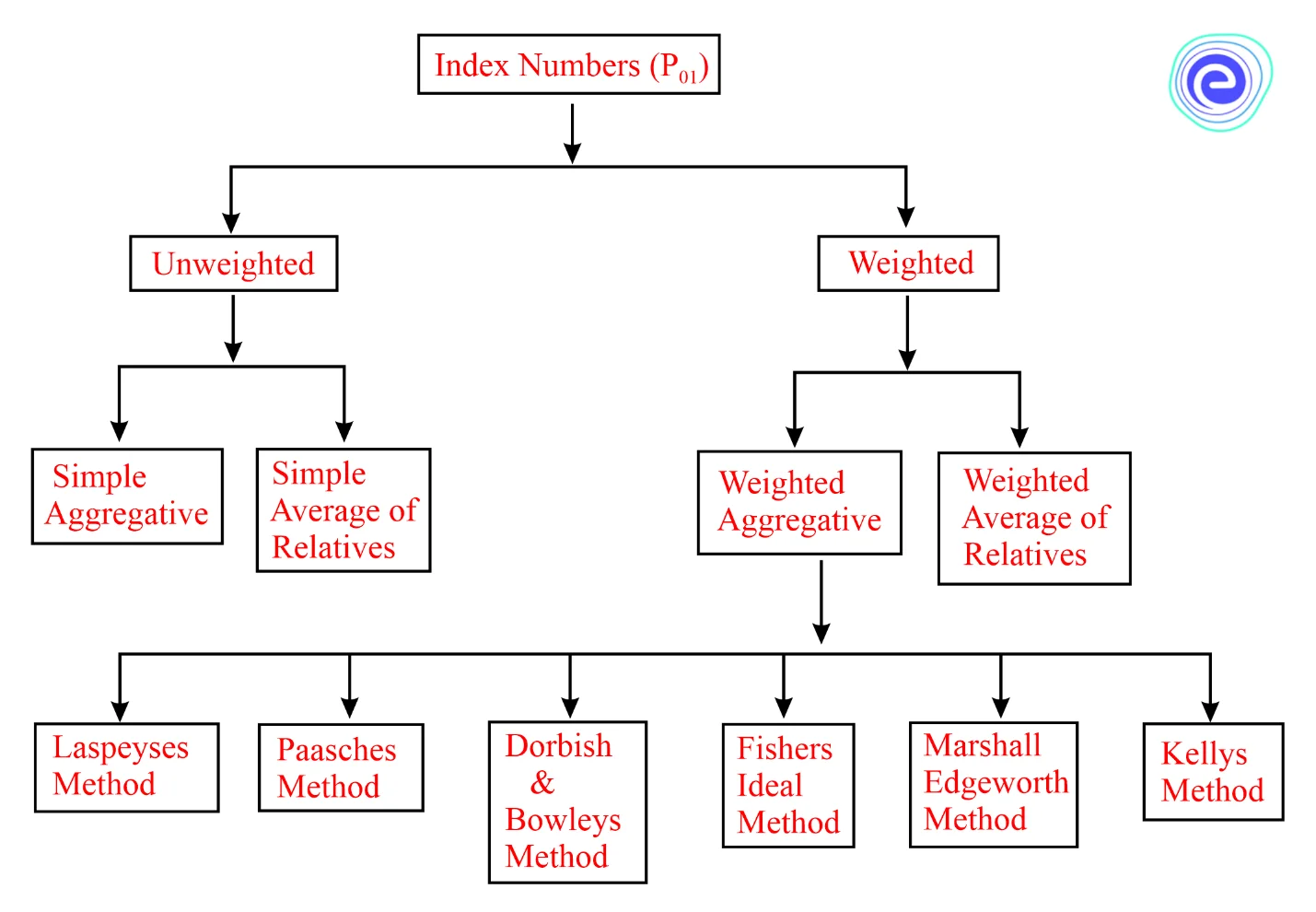
There are two types of quantity index numbers, such as
- Unweighted index numbers
- Weighted index numbers
There are various methods for calculating the quantity index numbers, such as a simple aggregate method, simple average method, Laspeyses method, Paasche’s method, Dorbish and Bowley’s method, Fisher’s ideal method, Marshall Edgeworth method and Kelly’s method.
3. Price Index
A price index calculates the average change in prices between periods or the average difference in prices between places. It is made up of a series of numbers that are arranged to compare the values for any two periods or places. It yields the average change in prices between periods or the average difference in prices between places. The general formula for calculating the price index numbers is given by
\({P_{1,\,2}} = f\left( {{P_1},\,{P_2},\,X} \right)\)
Here,
- \({P_{1,\,2}}\)- Price index from period \(1\) to period \(2\)
- \({{P_1}}\)-Price of goods in period \(1\)
- \({{P_2}}\)-Price of goods in period \(2\)
- \(X\)-Weights
a. Consumer Price Index Number
The consumer price index explains an average change in price by a certain category of client. As a result, it is completed for the current year’s services and goods. The cost-of-living index is also known as the CPI. This is because as the price level changes, so does the consumption pattern. CPI is divided into three categories. Agricultural laborer’s, industrial employees, and urban non-manual laborers are among them.
b. Wholesale Price Index Number
WPI simply measures the change in wholesale prices of commodities over time, as the name implies. Unlike the Consumer Price Index (CPI), which examines pricing changes from the consumer’s perspective, the Wholesale Price Index (WPI) examines price changes from the wholesale market’s perspective. As a result, it is a very important index.
Limitations of Index Numbers
Index numbers provide many benefits, but there is certain limitations it can undergo. The following are the limitations of index numbers:
- Since index numbers are derived from samples, there is a risk of errors. After much thought, these samples are put together, which creates the chance for errors.
- It is always done based on goods. Items chosen in this manner may not be in trend, resulting in an inaccurate analysis.
- Formulating index numbers can be done in different ways. Because of the variety of methodologies used, the results may present a different set of values, thus confusing the situation.
- The index numbers represent approximations of the relative changes that take place. Furthermore, changes in variables that are compared over a long period may be unreliable.
- The selection of representative commodities may be unbalanced because these products are based on samples.
Examples of Index Numbers
Q.1. What is the consumer price index? What are the prices measured by using the consumer price index number?
Ans:
There is a significant disparity in people’s purchasing patterns in society. To comprehend this pattern, we must first understand the prices paid by each sector. The index numbers we employ fall short of depicting the changes in most cases. We use the consumer price index (CPI) to understand this pattern.
The consumer price index explains an average change in price by a certain category of client. As a result, it is completed for the current year’s services and goods. The cost of living index is also known as the CPI. As the price level changes, so does the consumption pattern.
The two types of price indexes are measured with the help of the consumer price index. The Consumer Price Index for Urban Wage Earners and Clerical Workers (CPI-W) is the Consumer Price Index for Wage Earners and Clerical Workers. The Consumer Price Index for All Urban Consumers (CPI-U) is the Consumer Price Index for All Urban Consumers.
Q.2. What are the advantages of index numbers?
Ans:
Following are the some of advantages of index numbers:
- It helps deflate since it modifies primary data at different costs. It makes the transition from a nominal to a real wage easier.
- In Economics, index numbers help in formulating appropriate policies. Such discoveries also aid the establishment of research.
- It is useful when there are trends, such as drawing outcomes for irregular and cyclical forces.
- If economic activities develop in the future, index numbers can be used. This type of time series analysis is used to identify trends and cyclical patterns.
- The number can be used to track variations in the level of living in different countries across time.
Q.3. List the features of index numbers?
Ans:
The features of index numbers are listed below.
- It is an average used to quantify relative changes in situations when absolute measurements are not possible.
- The process of calculating index numbers varies from one variable to the next.
- It aids in comparing the levels of a phenomenon on a certain day to those on a previous date.
- It is a unique situation for averages, particularly for a weighted average.
- The use of index numbers is universal.
Q.4. List the uses of index numbers.
Ans:
The uses of index numbers are listed below:
- It aids in measuring changes in both the standard of living and the price level.
- Changes in the price level reflect in wage rate regulation.
- Wage rates may be altered when pricing levels are determined.
- The government’s policies are based on the price index number.
- Price stability is based on index numbers inherent in fiscal and economic policy.
- It serves as a starting point for worldwide comparisons of various economic factors, such as living standards between countries.
Q.5. Find the value index number for the given data:
| Items |
Base Year |
Current Year |
| Quantity |
Price |
Quantity |
Price |
| \(A\) |
\(3\) |
\(5\) |
\(2\) |
\(8\) |
| \(B\) |
\(7\) |
\(4\) |
\(5\) |
\(6\) |
| \(C\) |
\(4\) |
\(7\) |
\(3\) |
\(10\) |
| \(D\) |
\(6\) |
\(6\) |
\(5\) |
\(7\) |
Ans:
We know that the value index number is given by
\(\frac{{\sum {{p_1}} q_1}}{{\sum {{p_0}} {q_0}}} \times 100\)
\( = \frac{{2 \times 8 + 5 \times 6 + 3 \times 10 + 5 \times 7}}{{5 \times 3 + 4 \times 7 + 7 \times 4 + 6 \times 6}} \times 100\)
\( = \frac{{111}}{{107}} \times 100 = 103.74\)
Hence, value index number is \(103.74\)
Summary
One can construct a single measure of change for a large number of objects by estimating the index numbers. Price, quantity, volume, and other index numbers can all be determined. The formulas also show that the index numbers must be interpreted with caution. It is crucial to consider the elements to include and the time span. Their diverse applications show that index numbers are essential in policymaking. Price index number, value index number and quantity index numbers are some of the types of index numbers used to calculate the price, value and other quantities.
FAQs on Index Numbers
Students must have many questions with respect to Index Numbers. Here are a few commonly asked questions and answers.
Q.1. What do you mean by index numbers?
Ans: An index number is a mathematical measure that considers time, characteristics, and geographic location to describe changes in a set of related variables or just a single variable.
Q.2. How do you find the index numbers?
Ans: Index numbers are found by various methods. The main methods used to find the index numbers are simple aggregate and average methods.
Q.3. What are the main types of price index numbers?
Ans: The main two types of price index numbers are
- Consumer price index (CPI)
- Wholesale price index (WPI)
Q.4. What are the characteristics of index numbers?
Ans: Some characteristics of index numbers are
- It is a specialised average
- Measures the change over a given time period
- It is indicated in percentage form.
Q.5. What is a consumer price index number?
Ans: It is a figure that represents the average price change over time. In comparison to a base year, this price is paid by a specific class of consumers for products and services consumed in the current year.
LEARN EXAM CONCEPTS ON EMBIBE
We hope this information about Index Numbers has been helpful. If you have any doubts, comment in the section below, and we will get back to you soon.