Inverse Functions: Definition, Methods, Examples

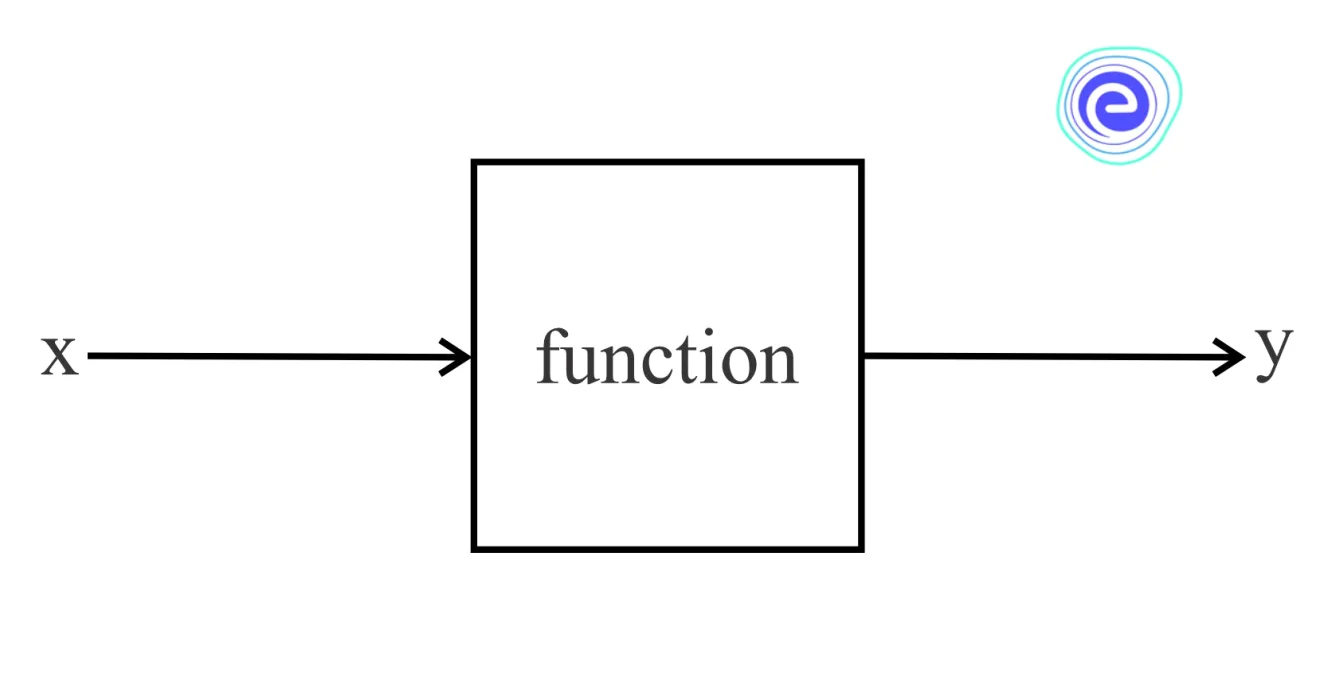
Inverse Functions: A function \(f\) from a set \(X\) to a set \(Y\) assigns exactly one element of \(Y\) to each element of \(X\). The set \(X\) is referred to as the domain of \(f\), and the set \(Y\) is the co-domain of \(f\). This function is called a one-to-one function. The inverse of a function \(f\) is something that undoes \(f\)’s operation.

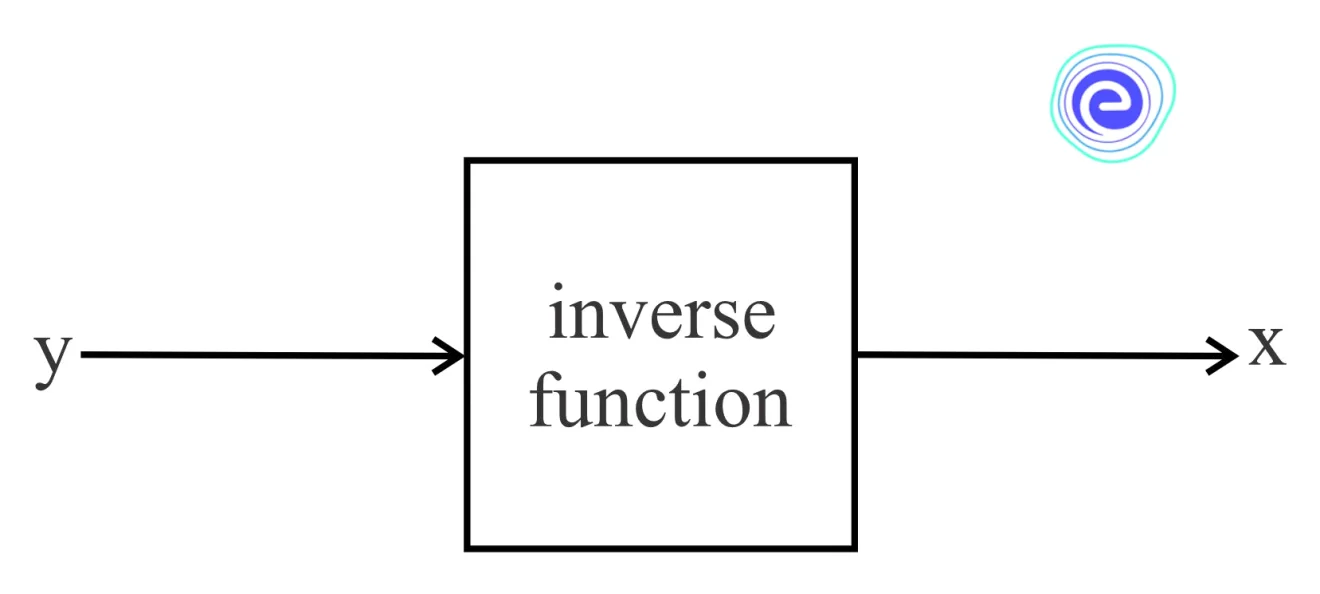
The inverse of \(f\) exists if and only if \(f\) is bijective, and the inverse is denoted by \({f^{ – 1}}\), if it exists. In Physics, Astronomy, navigation, construction, and many other fields, inverse functions are used. On a graph, the inverse of a function reflects the function’s graph over the line \(y = x\). In this article, let us learn about inverse functions, their representation, and the methods of calculation.

What are Inverse Functions?

Mathematically, functions are like a machine that takes an input value, processes it, and gives an output. There should only be one output that corresponds to each input.

Sometimes we have the output, while the input is unknown. In such cases, we must undo any processing or operation performed on the input. It is the same as undoing the function, which returns you to where you started.

If one function is to drive from home to the shop, the inverse function is to drive from the shop back to home.

A function begins with a value (input), then performs some operation on it, and the result is given out (output). The inverse function takes the output answer, performs some operations, and returns us to the starting value.

If \(f\) is one-one and onto, the inverse of \(f\), denoted by \({f^{ – 1}}\), exists. Many functions are not one-one, onto or both.  As a result, we cannot discuss their inverses. Note that the \(-1\) in inverse notation is not an exponent. Hence, we can say that

\({f^{ – 1}}(x) \ne \frac{1}{{f(x)}}\)

Example: Consider a graph of a \(f\) that has \((a,\,b)\) as one of its points. Then the graph of the inverse function will have \((b,\,a)\). An inverse of \(f\) is expressed as \({f^{ – 1}}\).

In essence, an inverse function swaps the first and second elements of each pair of the original function.

Are All Functions Invertible?

While talking about inverse functions, functions with a real-number domain and a real-number co-domain are considered. Then the next question that comes to mind is, are all functions invertible?

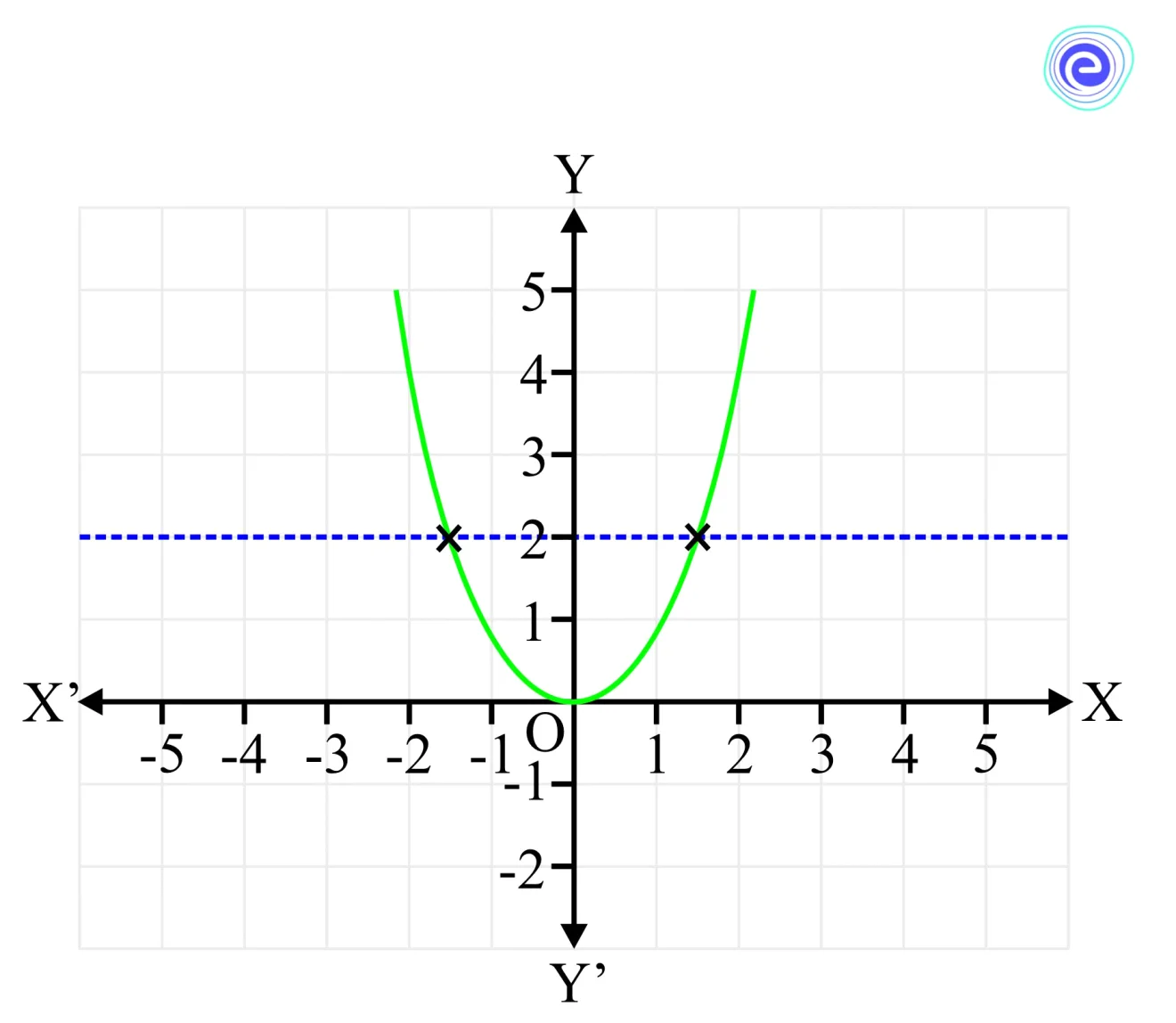
The immediate answer to this is a very well-known function that we have seen. That is \(f(x) = {x^2}\)

This function is not invertible because it fails to pass the horizontal line test.

Horizontal Line Test for \({x^2}\)

When a horizontal line is drawn across the graph of \({x^2}\) at \(y = 2\), the line is passed through 2 points. These two points correspond to two different values on the \(x-\)axis . This essentially means that it will give 2 when fed in both the corresponding \(x\) values.

Now, if this function is reverted, when we feed the value to 2, it can give two values for \(x\). So, the output is not unique. Therefore, this function is not invertible. For such functions, we cannot find the inverse functions.

However, suppose you restrict the domain of this function instead of the real line to only the positive half of the real line. In that case, the function will get one to one correspondence between the values on the \(x\) axis and \(y\) axis and then, we can talk about the inverse of this function when it is defined \([0\,{\rm{to}},\infty]\).

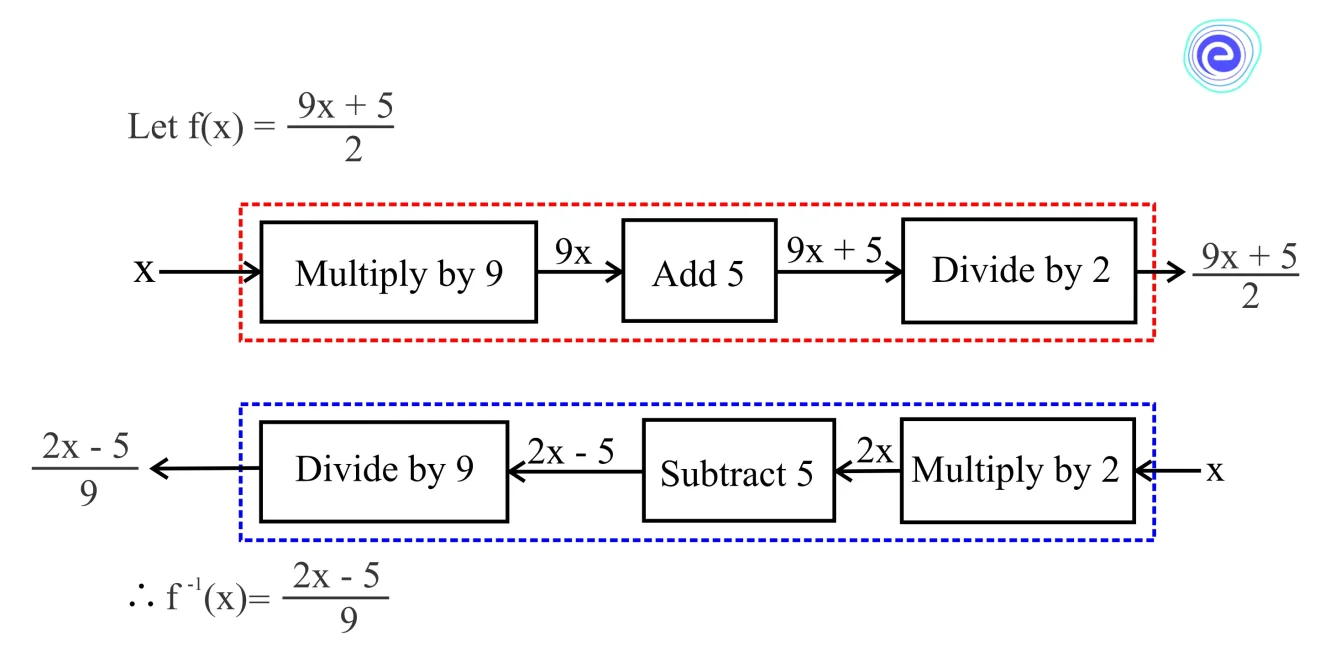
Inverting Functions

Consider the function \(f\left( x \right) = 4x – 8\). Here, multiply by 4 and then subtract 8 from the result. In the inverse function, however, we reverse the steps by first adding 8 to undo the subtraction and then dividing it by 4 to undo the multiplication.

Let us learn with another example.

Condition for Invertible Functions

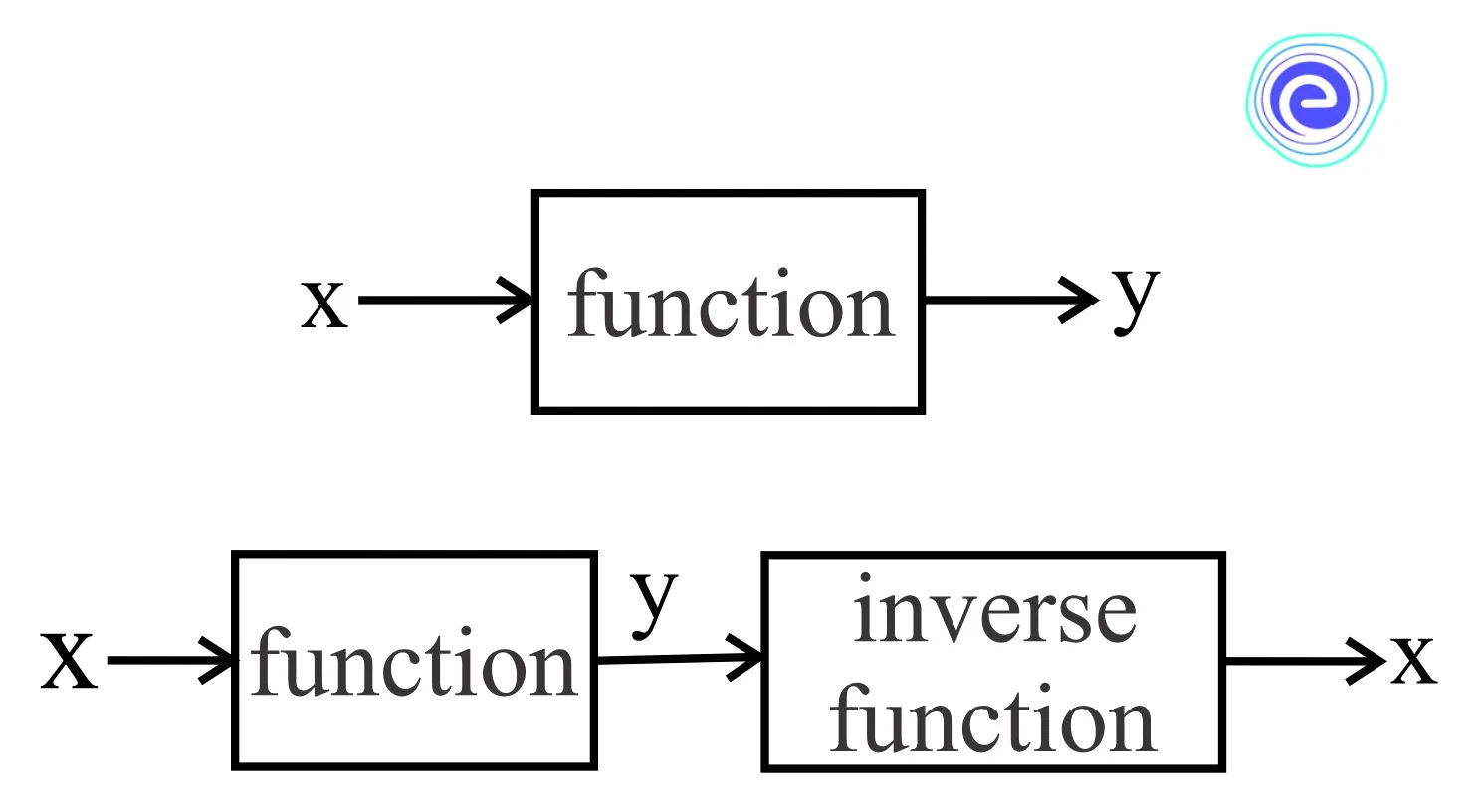
Given two one-to-one functions \(f(x)\) and \(g(x)\) if their composition is equal to the variable itself, then they are said to be inverses of each other. This relationship can be defined as,

\((f \circ g)(x) = (g \circ f)(x) = x\)

More specifically, we can say that \(g(x)\) is the inverse of \(f(x)\) and denote it by

\(g(x) = {f^{ – 1}}(x)\)

Likewise, we could also say that \(f(x)\) is the inverse of \(g(x)\) and denote it by

\(f(x) = {g^{ – 1}}(x)\)

The domain and range of two one-to-one functions have the following relations

• Domain of \({f^{ – 1}} = \) range of \(f\)
•  Range of \({f^{ – 1}} = \) domain of \(f\)

Methods to Find the Inverse

The different methods to find the inverse of a function are listed below.

1. Swapping the ordered pairs
2. Algebraic method
3. Graphical method

Swapping the Ordered Pairs

The ordered pairs of the inverse function are obtained by swapping the first and second elements of each coordinate in the function. Swap the \(x\) and \(y\) values when your function is defined as a list of ordered pairs. Remember that only if the original function is one-to-one will the inverse relation be a function.

Example: If the coordinates of the original function are \((1,\,2)\) and \(\left( { – 3,\, – 5} \right)\) the coordinates of the inverse function will be \((2,\,1)\) and \(\left( { – 5,\, – 3} \right)\)

Algebraic Method

For the function \(f\left( x \right)\), we can find its inverse function \({f^{ – 1}}(x)\) by following these steps:

Step 1: Substitute \(f\left( x \right)\) with \(y\). This helps us in the rest of the process.

Step 2: Substitute each \(x\) with a \(y\) and each \(y\) with an \(x\).

Step 3: Solve the equation for \(y\).

Step 4: Replace \(y\) by \(f\left( x \right)\),  since this is the inverse function.

Graphical Method

A function that reverses the effect produced by the original function is known as an inverse function. The main feature of the graphs of these functions is that they are reflections of the original functions over the line \(y = x\). The graphs of a function and its inverse are mirror images of each other.

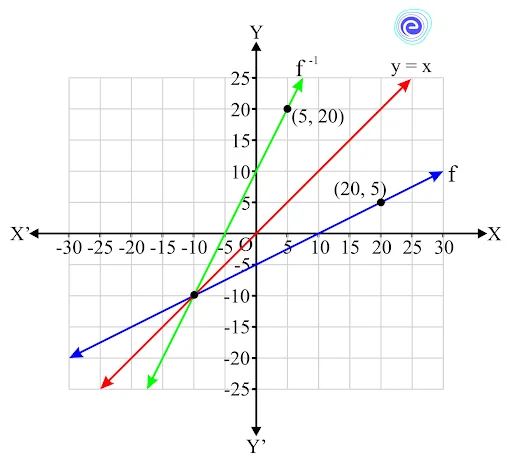
Example:

In this graph, we can see two functions which are inverse of each other. The lines \({f^{ – 1}}\) is obtained when we reflect the line \(f\) along the line \(y = x\). When we consider two points on \(f\) and \({f^{ – 1}}\), they will be swapped in ordered pairs. See the points \((20,\,5)\) on \(f\) and \((5,\,20)\) on \({f^{ – 1}}\). They are reflected over the line \(y = x\).

Solved Examples – Inverse Functions

Q.1. Check whether the function \(f(x) = 3x – 2\)  is an inverse of \(g(x) = \frac{{x + 3}}{2}\).
Ans: To check whether two functions are inverse of each other, we should get the value of the composition of functions as \(x\).
\((f \circ g)(x) = (g \circ f)(x) = x\)
\( \Rightarrow (f \circ g)(x) = f(g(x))\)
\( = f\left( {\frac{{x + 3}}{2}} \right)\)
\( = 3\frac{{x + 3}}{2} – 2\)
\( = \frac{{3(x + 3) – 4}}{2}\)
\( = \frac{{3x + 9 – 4}}{2}\)
\( = \frac{{3x + 5}}{2}\)
\(\therefore \,f(g(x)) \ne x\)
As \((f \circ g)(x)\) is not equal to \(x\), they are not inverse functions of each other.

Q.2. Find the inverse function if \(f(x) = \{ (13,\,4)(1,\, – 12)(15,\, – 11)(10,\,2)\} \)
Ans: Since \(x\) and \(y\) are used only once, the function and the inverse function are one-to-one functions.
The inverse of the function is obtained by swapping the value of the coordinates.
Therefore, the inverse function is given by
\({f^{ – 1}}(x) = \{ (4,\,13)( – 12,\,1)( – 11,\,15)(2,\,10)\} \)

Q.3. Find the inverse of the function \(f(x) = 2x – 3\).
Ans:
Step 1: Substitute \(f(x)\) with \(x\):
\(y = 2x – 3\)
Step 2: Swap the variables \(x\) and \(y\)
\(x = 2y – 3\)
Step 3: Solve the equation for \(y\):
\(2y = x + 3\)
\(y = \frac{{x + 3}}{2}\)
Step 4: Substitute \(y\) with \({f^{ – 1}}(x)\) :
\({f^{ – 1}}(x) = \frac{{x + 3}}{2}\)

Q.4. What is the inverse of the function \(f(x) = \frac{{x + 4}}{{2x – 5}}\)?
Ans:
Step 1: We have to substitute \(f(x)\) with \(y\):
\(y = \frac{{x + 4}}{{2x – 5}}\)
Step 2: We swap the variables \(x\) and \(y\):
\(x = \frac{{y + 4}}{{2y – 5}}\)
Step 3: We solve for \(y\) in the equation from step \(2\):
\(x\left( {2y – 5} \right) = y + 4\)
\( \Rightarrow 2xy – 5x = y + 4\)
\(2xy – y = 5x + 4\)
\({\rm{y}}\left( {2x – 1} \right)5x + 4\)
\(\therefore \,y = \frac{{5x + 4}}{{2x – 1}}\)
Step 4: We have to substitute \({f^{ – 1}}(x)\) with \(y\):
\({f^{ – 1}}(x) = \frac{{5x + 4}}{{2x – 1}}\)

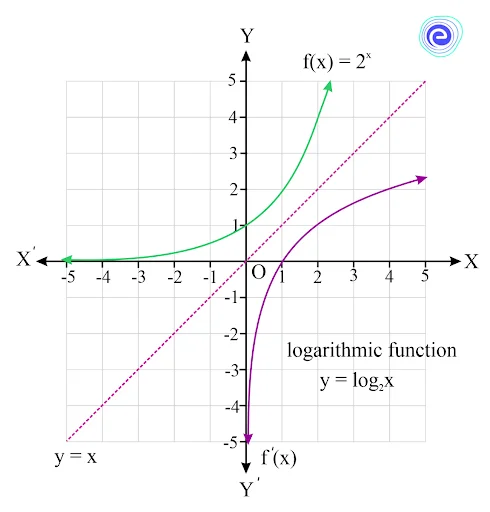
Q.5. Show the inverse of the exponential function, \(f(x) = {2^x}\) graphically.
Ans: We know that the main feature of inverse functions is that their graphs are reflections of the graphs of the functions over the line \(y = x\). The inverse function has the same coordinates as the original function, but the values of \(x\) and \(y\) are swapped. The inverse of an exponential function is a logarithmic function and their graphs are shown below.

Summary

The inverse of \(f\) is a function that undoes the operation of \(f\). The inverse of \(f\) exists if and only if \(f\) is bijective, and if it exists, it is denoted by \({f^{ – 1}}\). If f is invertible, then there is exactly one function \(g\) satisfying this property. If \(g\) is the inverse of \(f\), it is usually denoted as \({f^{ – 1}}\) Let f be a function whose domain is the set \(X\), and co-domain is the set \(Y\).

Then \(f\) is invertible if there exists a function \(g\) from \(Y\) to \(X\) such that \(g(x) = {f^{ – 1}}(x)\). If two functions are invertible, then their compositions will be equal to \(x\). That is, \(f\left( {f\left( x \right)} \right) = g(f(x)) = x\). Inverse functions are associative as well as commutative. The inverse of a function can be found algebraically or graphically. It is obtained by reflecting the points of the function over the line \(y = x\).

Frequently Asked Questions (FAQs)

Q.3. How can you find the inverse of a function with an exponent?
Ans: The inverse of an exponential function will be a logarithmic function. This is obtained by reflecting the points of exponential function along the line \(y = x\).

Q.4. Why do we need inverse functions?
Ans: One physically significant application of an inverse function is its ability to reverse a process to determine its input from the given output.
Assume you have an observation \(y\) that is the result of a process defined by the function \(f(x)\) with \((x\) being the unknown input. If you know (or can approximate with some accuracy) the function \((f(x)\) you can calculate the unknown \(x\) as \(({f^{ – 1}}(x)\).
This concept is critical in wireless communications, where the input is a symbol representing the information (bits), and the physical process is the wireless channel, which distorts the symbol. The basic approach to recovering the transmitted bits is to estimate and invert this channel.

Q.5. What are the properties of inverse functions?
Ans: The inverse of a function is thought to be a reflection of the original function over the line \(y = x\). The inverse function is obtained by swapping the original function’s \(\left( {x,\,y} \right)\) values as \(\left( {y,\,x} \right)\). An inverse function is represented as \({f^{ – 1}}\). For example, if \(f(x)\) and \(g(x)\) are inverses of each other, we can represent them as:
\({f^{ – 1}}(x) = g(x)\)
\(f(x) = {g^{ – 1}}(x)\)

Now that you have this detailed article on Inverse Functions, we hope you do your preparation well. If you face any issue or difficulty preparing for the exam, do let us know about it in the comments section and we will get back to you at the earliest.

Stay tuned to embibe for the latest updates on CBSE exam.