Lens Maker’s Formula

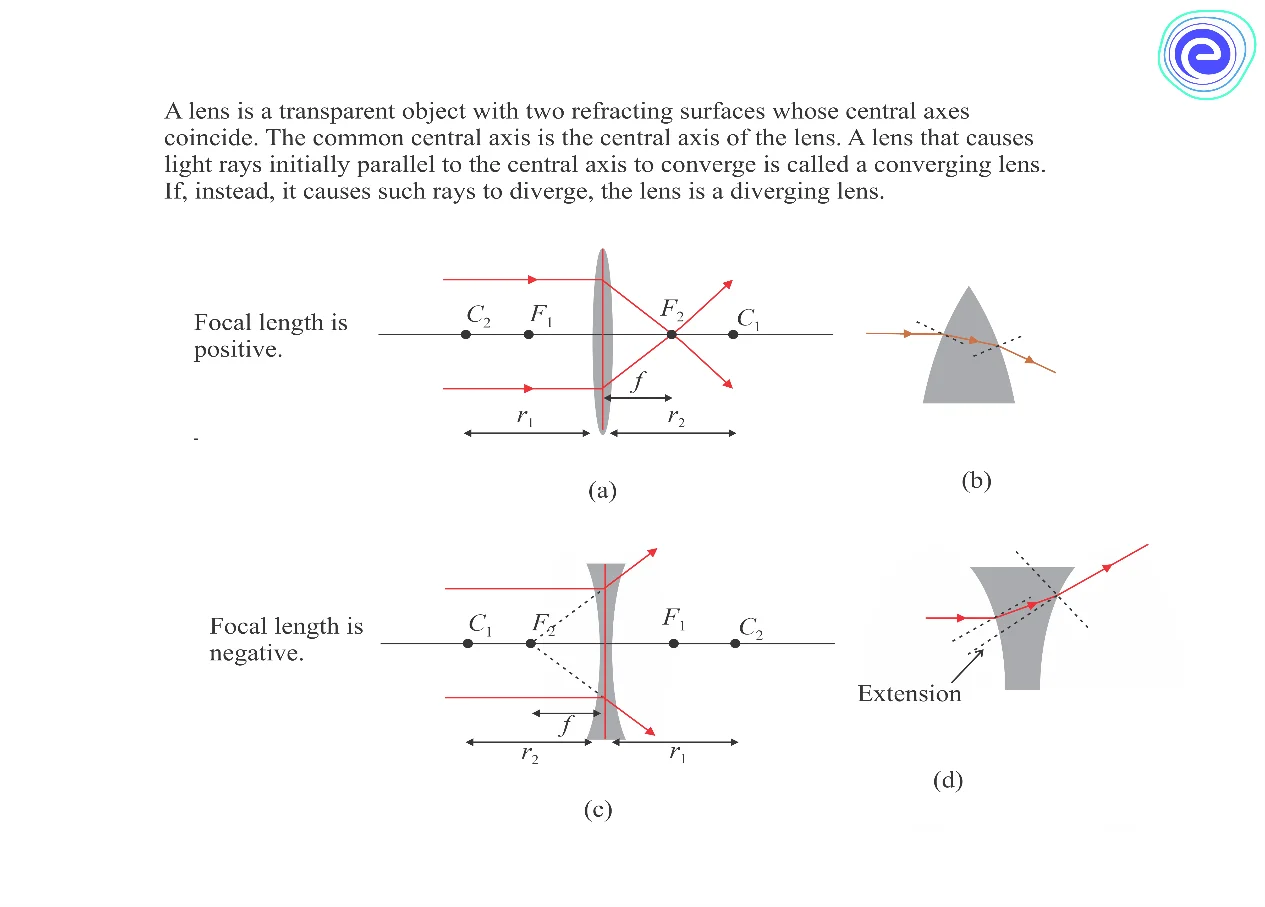
Lens Maker’s Formula: A transparent, refracting mediufm bound by two surfaces where at least one of the surfaces is curved is known as a lens. When the gap between the two bounded surfaces is small, it will be considered a thin lens.  The lens can be of two types: Converging or diverging. The focal length of a converging lens is positive, while the focal length of a diverging lens is negative. Thus, a convex lens does not always have to be converging, and a concave lens does not always have to be diverging. Lens maker’s formula help us to determine the value of an unknown quantity of a lens using the known values of other quantities.

Radius of Curvature and Focal Length of a Lens

A lens can consist of a pair of curved surfaces, or a plane surface joined to a curved surface. The curved surface of a lens is part of a sphere.

Radius of curvature: The radius of the glass sphere of which the surface of the lens is a part is called the radius of curvature of the given lens. Each lens has two radii of curvature. With the change in the shape of a lens, there will be a change in the radius of curvature.
Focal length: All the rays coming parallel to the principal axis of a lens, after refraction, either converge or appear to diverge from a point on the principal axis called the focus or principal focus. The distance between the optical centre and the focus of a lens is called the focal length. A lens’s focal length varies with the refractive index of the material of the lens and the radii of curvatures of the two surfaces.

The Lens Maker’s Formula

Lens maker’s formula defines a relation between the lens’s focal length, the refractive index of the material used to make the lens, and the radii of curvature of the two curved surfaces.  Lens manufacturers regularly use it to make lenses of the required focal length from glasses of different refractive indexes. In fact, opticians frequently use machines that work on this formula to design the glasses for us based on the power of our eyes.

Based on the curvature of the two optical surfaces, Lenses are of two types: Convex and concave.

We use the lens maker formula to construct a lens of the required focal length. A lens consists of two dissimilar curved surfaces. Thus, the focal length of the lens can be calculated if we are given the values of the refractive index and the radius of the curvature of both the surfaces and the thickness of the lens, using the lens maker’s formula as:

\(\frac{1}{f} = (\mu – 1) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}} + \left( {1 – \frac{1}{\mu }} \right)\frac{d}{{{R_1}{R_2}}}} \right]\)

Where:

\(f:\) is the focal length of the lens

\(\mu :\) refractive index

\({{R_1},{R_2}}:\) Radii of curvature

\(d:\) is the thickness of the lens

If the lenses are thin, the distance calculated from the poles of the two surfaces of the lens can be equated to the distances measured from the optical centre. Thus, substitute the thickness \(d=0\) in the above formula,

\(\frac{1}{f} = (\mu – 1) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right]\)

Sign convention

There is a sign convention that we all must follow while using the lens maker’s formula. For refraction at a curved surface:

1. The distances measured along the direction of the incident light are considered positive, while the distances in the opposite direction are negative.
2. The height above the principal axis is taken to be positive, while the heights measured below the principal axis are considered negative.

For convex lens:

\({R_1}:\) is positive

\({R_2}:\) is negative

\(f :\) is positive

For concave lens:

\({R_1}:\) is negative

\({R_2}:\) is positive

\(f :\) is negative

Lens Maker’s Formula Assumptions 

1. The lenses are considered to be thin.
2. All distances are measured from the optical centre of the given lens.
3. The aperture of a lens is assumed to be small.
4. The object is considered to be point-sized.
5. The angle between the incident ray and principal axis and the refracted ray and the principal axis is considered small.

Derivation of Lens Maker’s Formula

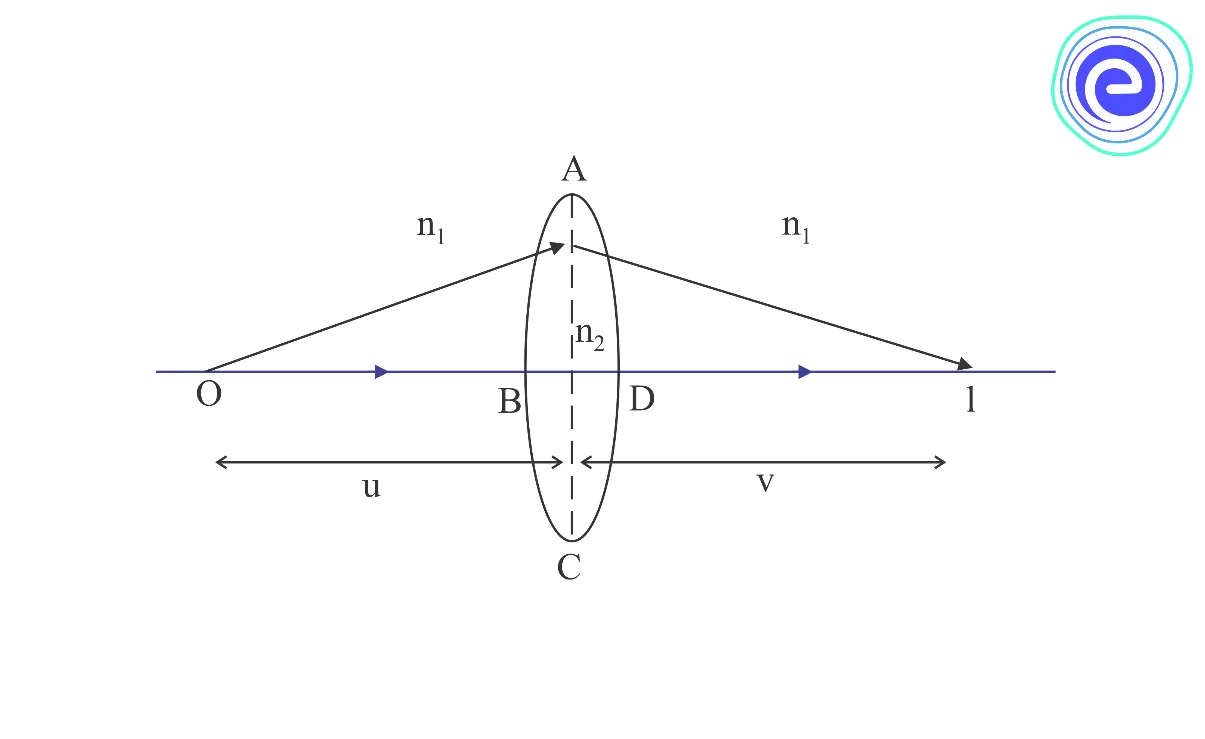
To derive the lens maker’s formula, consider the thin lens shown in the diagram given below:

It is a double convex lens made by two joining two identical spherical surfaces with a radius of curvature \(R.\) Let the refractive indices of the surrounding medium and the lens material be \({n_1}\) and \({n_2},\) respectively.

Let an object be placed in front of the lens at a distance \(u\) and let the image be formed at a distance \(v\) from the lens. 

We know, according to the formula for refraction of light on a spherical surface, 

\(\frac{{{n_2}}}{v} – \frac{{{n_1}}}{u} = \frac{{{n_2} – {n_1}}}{R}……..(1)\)

According to the diagram,

Object distance, \(OB=-u\)

Image distance, \(DI=+v\)

The radius of curvature of the glass\(=+R\)

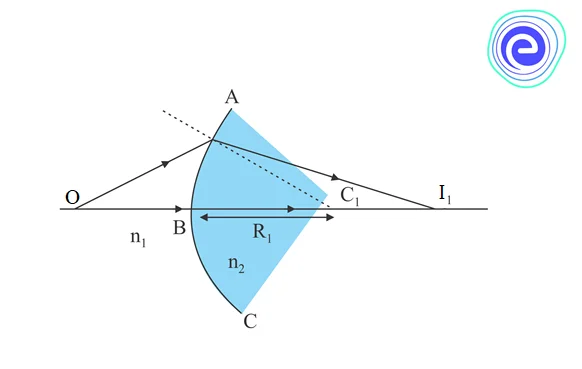
The image formation using the double convex lens occurs in two steps. The first refraction takes place at the lens interface \(ABC\) which will form the first image, marked as \({I_1}.\) The image obtained after the first refraction will serve as an object for the second refraction that occurs at the lens interface \(ADC.\)

Apply the equation \((1)\) for the interface \(ABC;\) we get:

\(\frac{{{n_2}}}{{B{I_1}}} – \frac{{{n_1}}}{{OB}} = \frac{{{n_2} – {n_1}}}{{B{C_1}}}…….\left( 2 \right)\)

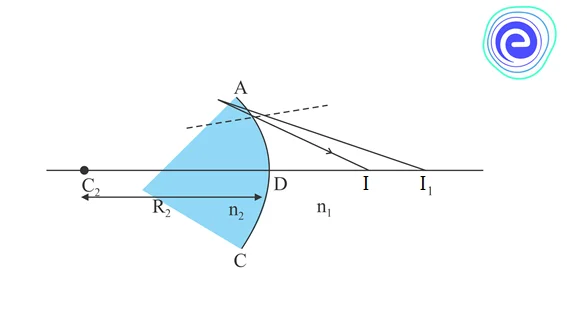
Now applying the equation \((1),\) for the second interface \(ADC,\) we get:

\(\frac{{{n_1}}}{{DI}} – \frac{{{n_2}}}{{D{I_1}}} = \frac{{{n_1} – {n_2}}}{{D{C_2}}} \ldots .(3)\)

It is assumed that the lens is thin,

Thus, \(B{I_1} = D{I_1}\)

Now, add the equations \((2)\) and \((3);\) we get:

\(\frac{{{n_1}}}{{DI}} – \frac{{{n_1}}}{{OB}} = \left( {{n_2} – {n_1}} \right)\left( {\frac{1}{{B{C_1}}} – \frac{1}{{D{C_2}}}} \right)\)

It is assumed that the object is placed at infinity. Thus, \(OB\) will be very large. 

Therefore. \(\frac{1}{{OB}} = 0\)

\(\therefore \frac{{{n_1}}}{{DI}} = \left( {{n_2} – {n_1}} \right)\left( {\frac{1}{{B{C_1}}} – \frac{1}{{D{C_2}}}} \right)\)

Dividing both sides of the equation by \({n_1},\) we get:

\(\frac{1}{{DI}} = \left( {\frac{{{n_2}}}{{{n_1}}} – 1} \right)\left( {\frac{1}{{B{C_1}}} – \frac{1}{{D{C_2}}}} \right)\)

Use the values:

\(D{C_2} = {R_2},B{C_1} = {R_1}\) and \(DI=f\)

Substitute these values into the above equation, we get:

\(\frac{1}{f} = \left( {\frac{{{n_2}}}{{{n_1}}} – 1} \right)\left( {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right)\)

This is the Lens Maker’s formula.

Problems Based on Lens Maker’s Formula

Q.1. The focal length of a lens, made up of glass, is \({\rm{15}}\,{\rm{cm}}\) in the air. What would be the focal length of the same lens in water? It is given the refractive indices of glass and water are \(1.51\) and \(1.33,\) respectively.
Ans: Let the radii of curvature of the lens be \({R_1}\) and \({R_2}\)
The focal length of the lens in the air: \({f_a} = 15\;{\rm{cm}}\)
The focal length of the lens in the water: \({f_w} = ?\)
The refractive index of glass \({n_2} = 1.51\)
The refractive index of water \({n_1} = 1.33\)
Applying lens maker equation for air,
\(\frac{1}{{{f_a}}} = \left( {{n_2} – 1} \right) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right]\)
\(\frac{1}{{15\;{\rm{cm}}}} = (1.51 – 1) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right]\)
\(\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}} = \frac{1}{{7.65}}\)
Applying lens maker equation for water,
\(\frac{1}{{{f_w}}} = \left( {\frac{{{n_2}}}{{{n_1}}} – 1} \right)\left( {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right)\)
\(\frac{1}{{{f_w}}} = \left( {\frac{{1.51}}{{1.33}} – 1} \right) \times \left[ {\frac{1}{{7.65}}} \right]\)
\(\frac{1}{{{f_w}}} = 0.01769\)
\({f_w} = 56.53\;{\rm{cm}}\)

Q.2. Find out the focal length of the lens whose refractive index is \(2.\) It is given that the radius of curvatures of each surface is \({\rm{20}}\,{\rm{cm}}\) and \({\rm{-35}}\,{\rm{cm}},\) respectively.
Ans: We are given that:
\(n=2\)
\({R_1} = 20\;{\rm{cm}}\)
\({R_2} = 35\;{\rm{cm}}\)
Applying the lens maker’s formula is:
\(\frac{1}{f} = (n – 1) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right]\)
\(\frac{1}{f} = (2 – 1) \times \left[ {\frac{1}{{20}} – \frac{1}{{( – 35)}}} \right]\)
\(\frac{1}{f} = \left[ {\frac{{ – 55}}{{( – 35 \times 20)}}} \right]\)
\(\frac{1}{f} = 0.078\)
\(f = 12.82\;{\rm{cm}}\)

Summary

Lens maker’s formula defines a relation between the lens’s focal length, the refractive index of the material used to make the lens, and the radii of curvature of the two curved surfaces.  Lens manufacturers regularly use it to make lenses of the required focal length from glasses of different refractive indexes.

The focal length of the lens can be calculated if we are given the values of the refractive index and the radius of the curvature of both the surfaces and the thickness of the lens, using the lens maker’s formula as:

\(\frac{1}{f} = (\mu – 1) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}} + \left( {1 – \frac{1}{\mu }} \right)\frac{d}{{{R_1}{R_2}}}} \right]\)

If the lenses are thin, then the focal length of the lens can be given as:

\(\frac{1}{f} = (\mu – 1) \times \left[ {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right]\)

Frequently Asked Questions on Lens Maker’s Formula

Q.1. What is a lens?
Ans: The lens is a transparent refractive medium formed by joining two surfaces with either two curved surfaces or a curved and a plane surface.

Q.2. Give the lens maker’s formula for a double convex lens.
Ans: Lens maker’s formula for a double convex lens: \(\frac{1}{f} = \left( {\frac{{{n_2}}}{{{n_1}}} – 1} \right)\left( {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right)\)

Q.3. Define the radius of curvature of the lens.
Ans: The radius of the sphere of which the surface of the lens is a part is called the radius of curvature of the lens. A lens has two radii of curvatures.

Q.4. Give the relation between focal length and radius of curvature of a lens.
Ans: \(\frac{1}{f} = \left( {\frac{{{n_2}}}{{{n_1}}} – 1} \right)\left( {\frac{1}{{{R_1}}} – \frac{1}{{{R_2}}}} \right)\)

Q.5. What are the distances opposite to the direction of motion of incident light rays are considered to be?
Ans: The distances opposite to the direction of motion of incident light rays are considered to be negative.

Learn about Optical Centre here

We hope you find this article on ‘Lens Maker’s Formula‘ helpful. In case of any queries, you can reach back to us in the comments section, and we will try to solve them.