Limits of Trigonometric Functions: Definition, Formulas, Examples

Limits of Trigonometric Functions: Limits indicate how a function behaves when it is near, rather than at, a point. Calculus is built on the foundation of this basic yet strong principle. Trigonometric functions in Mathematics link an angle to ratios of two side lengths in a right-angled triangle.

The six basic trigonometric functions are as follows: sine, cosine, tangent, cotangent, secant, and cosecant. The limits of trigonometric functions describe how it behaves at different points. Each trigonometric function tending to a point has a limit that may be estimated based on the function’s continuity over its domain and range. The limit of each trigonometric function at the same position is different, and can be seen in the graph of each function.

Uses of Trigonometric Functions

Trigonometric functions are widely employed in all geodetic studies, including navigation, solid mechanics, celestial mechanics, geodesy, and many more. They are one of the simplest periodic functions, and as a result, they are frequently used in Fourier analysis to examine periodic phenomena.

We know that the ratio of the sides of a right-angled triangle is the basis for trigonometric functions and identities. The perpendicular side, hypotenuse, and base of a right triangle are employed in trigonometric formulas to determine the sine, cosine, tangent, secant, cosecant, and cotangent values.

What are the Limits of a Function?

A limit of a function is a value that the function approaches as the input approaches a certain value. Limits define continuity.

Suppose \(f\) is a real-valued function and \(c\) is a real number. Then, the expression
\(\mathop {\lim }\limits_{x \to c} f(x) = L\)

means that \(f(x)\) can be made to be as close to \(L\) as desired, by making \(x\) sufficiently close to \(c\). This is read as “the limit of \(f\)of \(x\), as \(x\) approaches \(c\), is \(L\)”

What are the Limits of Trigonometric Functions?

The limit of each trigonometric function tending to a point can be evaluated according to the function’s continuity considering its domain and range.

We can find these limits by evaluating the function as \(x\) approaches \(0\) on the left and the right, i.e., by evaluating the two one-sided limits.

Note that the basic \(6\) trigonometric functions are periodic and do not approach a finite limit as \(x \to  \pm \infty \).

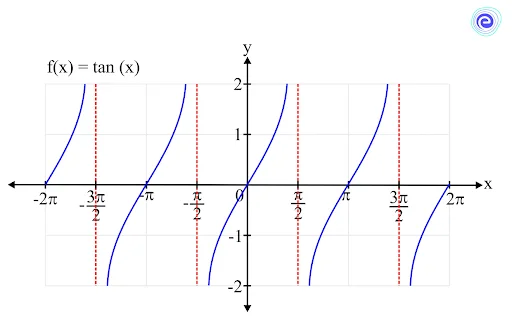
Example: While \(\sin x\) oscillates between \(1\) and \(-1\), \(\tan x\) has an infinite number of vertical asymptotes as  \(x \to  \pm \infty \) Hence, it does not approach a finite limit, nor does it approach \( \pm \infty \) as \(x \to  \pm \infty \)

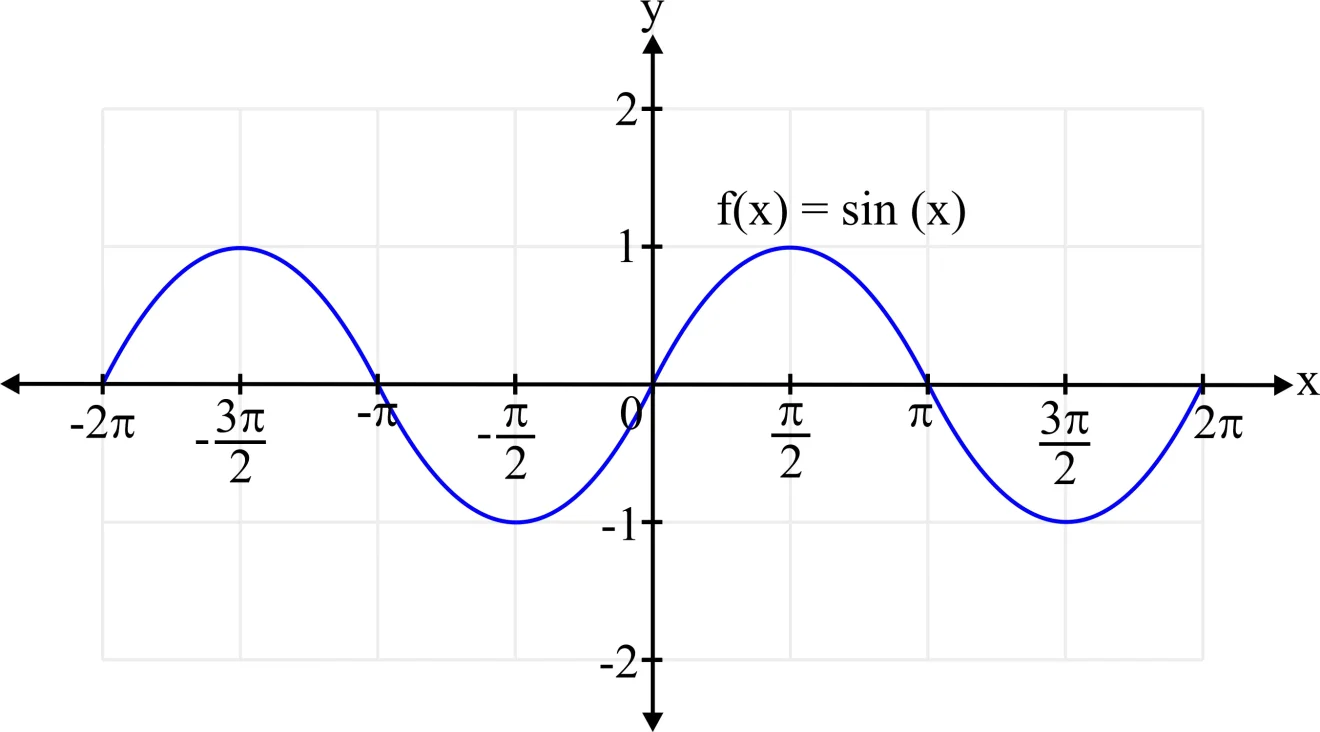
Limits of a Sine Function

Following are some of the limits of Sine Function

The function \(f(x) = \sin \left( x \right)\) is a continuous function over its entire domain, and the domain consists of all real numbers. The range of sine function is \(\left[ { – 1,1} \right]\).

Therefore, \(\mathop {\lim }\limits_{x \to c}\,\sin (x) = \sin (c)\)

So, if the limit of the sine function is found at any real value, it is always defined and lies between \(\left[ { – 1,1} \right]\).

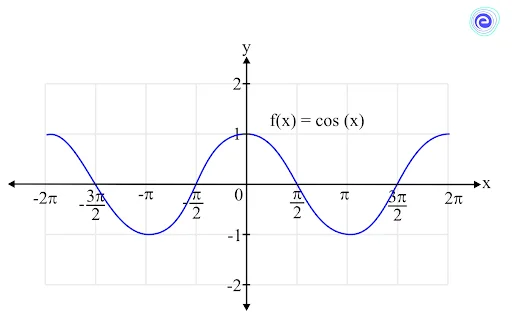
Limits of a Cosine Function

The function \(f(x) = \cos \left( x \right)\) is a continuous function over its entire domain, and the domain consists of all real numbers.

The range of the cosine function is \(\left[ { – 1,1} \right]\).

So, if the limit of the \(\cos\) function is found at any real value, it is always defined and lies between \(\left[ { – 1,1} \right]\).

Note:

• The graphs of the functions \(y = \sin x\) and \(y = \cos x\) approach different values between \(-1\) and \(1\).
• The function oscillates between the values, so it is impossible to find the limit of \(y = \sin x\), and \(y = \cos x\) as \(x\) tends to \( \pm \infty \).
• Hence, we use the sandwich theorem in such cases.

Limit of a Tangent Function

The function \(f(x) = \tan \left( x \right)\) is defined at all the real numbers except the values where \(\cos \left( x \right)\) is equal to \(0\), that is, the values \(\frac{\pi }{2} + \pi n\) for all integers \(n\).

Hence, its domain is all real numbers except \(\frac{\pi }{2} + \pi n,\,n \in Z\).

The range of the tangent function is \(( – \infty , + \infty )\)

The limit of the tangent function can be calculated in its domain. It is always defined and lies between \(( – \infty , + \infty )\)
\(\mathop {\lim }\limits_{x \to c} \tan (x) = \tan (c)\)

 where \(c\) is a real number except \(\frac{\pi }{2} + \pi n,\,n \in Z\)

PRACTICE EXAM QUESTIONS AT EMBIBE

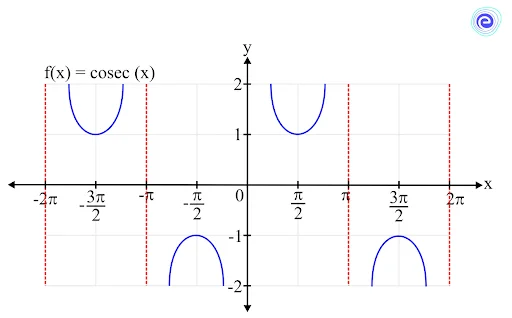
Limit of a Cosecant Function

The function \(f(x) = {\mathop{\rm cosec}\nolimits} (x)\) is defined at all the real numbers except the values where \(\sin \left( x \right)\) is equal to \(0\), that is, the values \(\pi n\) for all integers \(n\). So, the domain is all the real numbers except \(\pi n,\,n \in Z\)

The range of the cosecant function is \(( – \infty , – 1] \cup [1, + \infty )\)

The limit of the cosecant function can be calculated in its domain. It is always defined and lies within its range.
\(\mathop {\lim }\limits_{x \to c} {\mathop{\rm cosec}\nolimits} (x) = {\mathop{\rm cosec}\nolimits} (c)\)

 where \(c\) is a real number except for \(\pi n,\,n \in Z\).

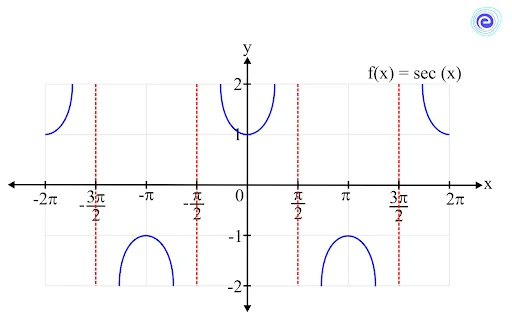
Limit of a Secant Function

The function \(f(x) = \sec \left( x \right)\) is defined at all the real numbers except the values where \(\cos (x)\) is equal to \(0\), that is, the values \(\frac{\pi }{2} + \pi n\) for all integers \(n\). So, the domain is all the real numbers except \(\frac{\pi }{2} + \pi n,\,n \in Z\).

The range of the function is \(( – \infty , – 1] \cup [1, + \infty )\).

The limit of the secant function can be calculated in its domain. It is always defined and lies within its range.
\(\mathop {\lim }\limits_{x \to c} \sec (x) = \sec (c)\)

where \(c\) is a real number except for \(\frac{\pi }{2} + \pi n,\,n \in Z\).

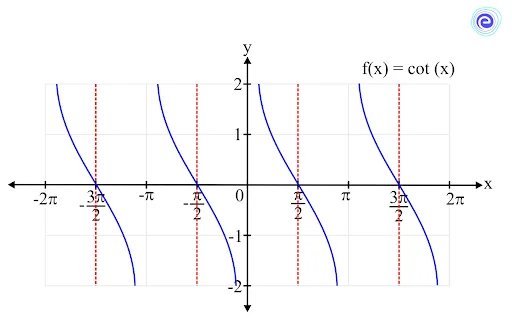
Limit of a Cotangent Function

The function \(f(x) = \cot \left( x \right)\) is defined at all the real numbers except the values where \(\tan \left( x \right)\) is equal to \(0\), that is, the values \(\pi n\) for all integers \(n\). So, the domain is all the real numbers except \(\pi n,\,n \in Z\)

The range of the function is \(( – \infty , + \infty )\)

The limit of the cotangent function can be calculated in its domain. It is always defined and lies within its range.
\(\mathop {\lim }\limits_{x \to c} \cot (x) = \cot (c)\)

where \(c\) is a real number except for \(\pi n,\,n \in Z\).

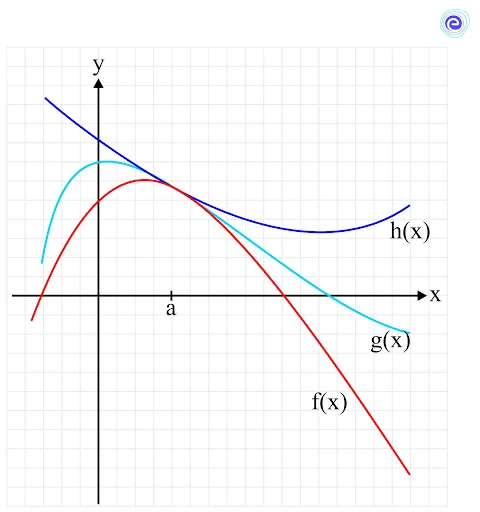
Sandwich Theorem or Squeeze Theorem

The sandwich theorem is used to calculate the limit of those functions whose limit cannot be calculated easily, like \(g(x) = \frac{{\sin x}}{x}\) at \(x=0\).

In this case, the function \(g(x)\) is squeezed or sandwiched between two functions \(h(x)\) and \(f(x)\) in such a way that
\(f(x) \le g(x) \le h(x)\)

The graph for such a condition can be visualised as below.

We can say \(h(x)\) is the upper limit of \(g(x)\) and \(f(x)\) is its lower limit at a point \(a\), as seen in the graph.

If \(\mathop {\lim }\limits_{x \to a} h(x) = L\) and \(\mathop {\lim }\limits_{x \to a} f(x) = L\)

where,
\(a\) is the point at which the limit is being calculated
\(L\) is the value of the limit

Then,

\(\mathop {\lim }\limits_{x \to a} g(x) = L\)

Two trigonometric limits found so are

\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\)

\(\mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{x} = 0\)

Solved Examples – Limits Trigonometric Functions

Below are a few solved examples that can help in getting a better idea.

Q.1. Evaluate the limit, \(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x}}{{\sin x – 3}}\)
Solution: We can find the limit by direct substitution.
Substituting \(0\) for \(x\), we get that \({\cos x}\) approaches \(1\) and \({\sin x – 3}\) approaches \(-3\). Hence,
\(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x}}{{\sin x – 3}} = \frac{1}{3}\)

Q.2. Evaluate the limit \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 5x}}{x}\)
Solution: Using the sandwich theorem, we know that
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\)
To evaluate the given limit, we have to modify the given function corresponding to this limit.
So, multiply the numerator and the denominator by \(5\). We get
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 5x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin 5x}}{x} \times \frac{5}{5}\)
\( = \mathop {\lim }\limits_{x \to 0} 5\mathop {\lim }\limits_{x \to 0} \frac{{\sin 5x}}{{5x}}\)
\( = 5 \times 1\)
\(=5\)

Q.3. Evaluate the limit \(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x}}{{\cos x + \pi }}\)
Solution: We can find the limit by direct substitution.
Substituting \(0\) for \(x\), we get that \({\cos x}\) approaches \(1\) and \({\cos x + \pi }\) approaches \(\pi \).
\(\therefore \mathop {\lim }\limits_{x \to 0} \frac{{\cos x}}{{\cos x + \pi }} = \frac{1}{\pi }\)

Q.4. Evaluate the limit \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{{3x}}\).
Solution: Using the sandwich theorem, we know that
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\)
So, to evaluate the given limit, we have to modify the given function corresponding to this limit.
So, \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{{3x}}\) can be modified as
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{{3x}} \times \frac{2}{2} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{{2x}} \times \frac{2}{3}\)
\( = \mathop {\lim }\limits_{x \to 0} \frac{2}{3}\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{{2x}}\)
\( = \frac{2}{3} \times 1\)
\( = \frac{2}{3}\)

Q.5. Evaluate \(\mathop {\lim }\limits_{x \to 0} \frac{{\sec x – 1}}{x}\)
Solution: We know that \(\sec x = \frac{1}{{\cos x}}\)
So, \(\mathop {\lim }\limits_{x \to 0} \frac{{\sec x – 1}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{1}{{\cos x}} – 1}}{x}\)
\( = \mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{x\cos x}}\)
\( = \mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{{\cos x}}} \right)\left( {\frac{{1 – \cos x}}{x}} \right)\)
\( = \mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{{\cos x}}} \right)\lim \left( {\frac{{1 – \cos x}}{x}} \right)\)
\( = 1 \times 0\)
\(=0\)

Summary

We can discover the limit of any trigonometric function using direct substitution. These limits can be found by evaluating the function as \(x\) approaches \(0\) on both sides, i.e. assessing two one-sided limits. The graphs of the functions \(y = \sin x\) and \(y = \cos x\) approach different values between \(-1\) and \(1\). The function value oscillates between the \(-1\) and \(1\) values, so it is impossible to find the limit of \(y = \sin x\), and \(y = \cos x\) as \(x\) tends to \( \pm \infty \). The sandwich theorem is y useful for establishing basic trigonometric limits in such cases. This theorem calculates limits by squeezing or sandwiching a function, with a limit at a point \(a\) that is unknown, between two functions having a common limit at \(a\).

Frequently Asked Questions (FAQs)

Students might be having many questions regarding the Limits of Trigonometric Functions. Here are a few commonly asked questions and answers.

Q.1. What is the limit of a sine function?
Ans: The function \(f(x) = \sin \,(x)\) is a continuous function over its entire domain, and the domain consists of all real numbers. The range of sine function is \(\left[ { – 1,1} \right]\).
Therefore, \(\mathop {\lim }\limits_{x \to c} \sin (x) = \sin (c)\)
So, if the limit of the sine function is found at any given real value, it is always defined and lies between \(\left[ { – 1,1} \right]\)

Q.2. What are the limits of cos?
Ans: The function \(f(x)=\cos (x)\) is a continuous function over its entire domain, and the domain consists of all real numbers.
The range of the cosine function is \(\left[ { – 1,1} \right]\).
So, if the limit of the cos function is found at any real value, it is always defined and lies between \([-1,\,1]\).
The graphs of the functions \(y = \sin x\) and \(y = \cos x\) approach different values between \(-1\) and \(1\). The function oscillates between the values, so it is impossible to find the limit of \(y = \sin x\), and \(y = \cos x\) as \(x\) tends to \( \pm \infty \).
Hence, we use the sandwich theorem in such cases

Q.3. Do all functions have limits?
Ans: Limits (limits of a function) is a fundamental notion in calculus that deals with the value of a function at a certain point termed a limit. The definite integral of the function is calculated using limits. Limits aren’t present in all functions. Because the variable approaches to infinity, some functions have no limit.

Q4. Can cos be infinity?
Ans: Sin and cos functions have values ranging from \(-1\) to \(1\). They have no precise values assigned to them. The values of \(\sin x\) and \(\cos x\) are always between \(-1\) and \(1\). Also, because \(\infty \) is undefined, \(\sin (\infty)\) and \(\cos (\infty )\) cannot have precise values.

Q.5. Do tan functions have limits?
Ans: The function \(f(x)=\tan (x)\) is defined at all the real numbers except the values where \(\cos (x)\) is equal to \(0\), that is, the values \(\frac{\pi }{2} + \pi n\) for all integers \(n\). Hence, its domain is all real numbers except \(\frac{\pi }{2} + \pi n,n \in Z\).
The range of this function is \(( – \infty ,\,+ \infty )\).
The limit of the tangent function can be calculated in its domain and it is always defined and lies between \((-\infty,+\infty)\).
\(\mathop {\lim }\limits_{x \to c} \tan (x) = \tan (c)\)
where \(c\) is a real number except \(\frac{\pi }{2} + \pi n,n \in Z\)

We hope this information about the Limits of Trigonometric Functions. If you have any doubts, comment in the section below, and we will get back to you.