Pascal’s Law – Formula, Application and Derivation

Pascal’s Law is a principle in fluid mechanics that tells us how pressure at various points inside a stationary liquid changes when the pressure at some point is changed. It was given by Blaise Pascal. This law has many applications in the design and construction of many heavy machineries as well as some simple tools used in our daily lives. A hydraulic press would be an example of heavy machinery, and a hydraulic car jack would be an example that many of us have used. So, what is Pascal’s law, what are its applications, what is the working principle behind a hydraulic press and a hydraulic car jack? To answer all these questions, let us understand Pascal’s law in detail.

What is Pascal’s Law?

Pascal’s law states that if pressure changes by some value at a point in an incompressible confined liquid, then the pressure changes at every point inside the liquid by the same value. It simply means that when we apply pressure at a point in an enclosed fluid, the change in pressure is transmitted everywhere in the fluid in all directions. So in a way, when we apply a force at one point in a confined liquid, its effect will be felt at other points too.

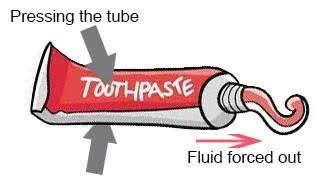
To understand this, let us take a daily example. When we squeeze a toothpaste, the paste comes out of the small opening. It does not matter where we press it. The paste is a fluid that is held in a closed container. Pressure applied at any point is transferred in all directions, and it comes out of the only opening present in the tube.

Definition of Pressure

Pressure means the force applied perpendicularly per unit area.

\({\rm{Pressure}}(P) = \frac{{{\rm{ Force }}(F)}}{{{\mathop{\rm Area}\nolimits} (A)}}\)

SI unit of pressure is \({\rm{pascal}}\). A force of \(1\;{\rm{N}}\) over an area of \(1\;{{\rm{m}}^2}\) is \(1\) \({\rm{pascal}}\).

\({\rm{1}}{\mkern 1mu} \,{\rm{pascal = }}\frac{{{\rm{1}}\,{\rm{newton}}}}{{{\rm{1}}\,{{\rm{m}}^{\rm{2}}}}}\)

Proof of Pascal’s Law

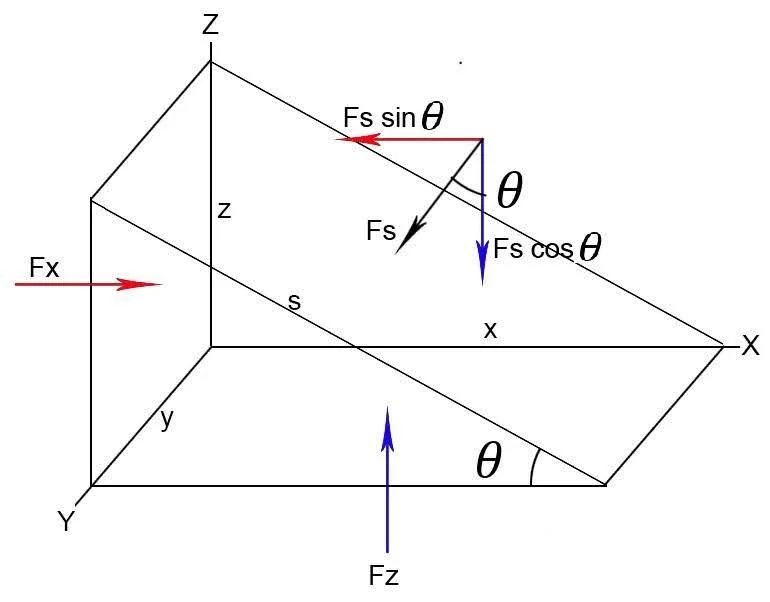
To prove that the change in pressure inside a fluid is the same in all directions, let us consider a tiny volume in the shape of a triangular prism. One face is inclined at an angle \(\theta \) with the horizontal.

We consider three rectangular faces of the prism.
\({F_x}\) is the force acting on the face on the \(YZ\) plane. Its area is \(y \times z\).
\({F_z}\) is the force acting on the face on the \(XY\) plane. Its area is \(x \times y\).
\({F_s}\) is the force acting on the inclined face. Its area is \(s \times y\).

From the right-angled triangle,

\(\sin {\rm{\theta }} = \frac{z}{s}\)

and

\(\cos \,{\rm{\theta }} = \frac{x}{s}\)

\({\rm{force = pressure \times area}}\)
\({F_x} = {P_x} \times y \times z\)
\({F_z} = {P_z} \times x \times y\)
\({F_s} = {P_s} \times s \times y\)

Since \({F_s}\) is inclined at an angle, we take its \(x\) and \(y\) coordinate values as \({F_s}\sin {\rm{\theta }}\) and \({F_s}\cos {\rm{\theta }}\).

Upward \({F_z}\) and downward \({F_s}\cos \,{\rm{\theta }}\) are equal and opposite.

Equating them,

\({F_z} = {F_s}\cos \,{\rm{\theta }}\)
\({P_x}yz = {P_s}sy \times \frac{z}{s}\)
\({P_z} = {P_s}\)

Rightward \({F_x}\) and leftward \({F_s}\sin \,{\rm{\theta }}\) are equal and opposite.
Equating them,

\({F_x} = {F_s}\sin \,{\rm{\theta }}\)
\({P_x}yz = {P_s}sy \times \frac{z}{s}\)
\({P_x} = {P_s}\)

This means that,

\({P_x} = {P_z} = {P_s}\)

It proves Pascal’s law that the pressure acting in all directions is the same.

Applications of Pascal’s Law

Pascal’s law has many practical applications in industries and vehicles. Transmission of force and multiplication of force are the main applications.

Hydraulic Press or Lift

A hydraulic press achieves multiplication of force many times over the amount applied. A small force applied is magnified many times in a hydraulic press.

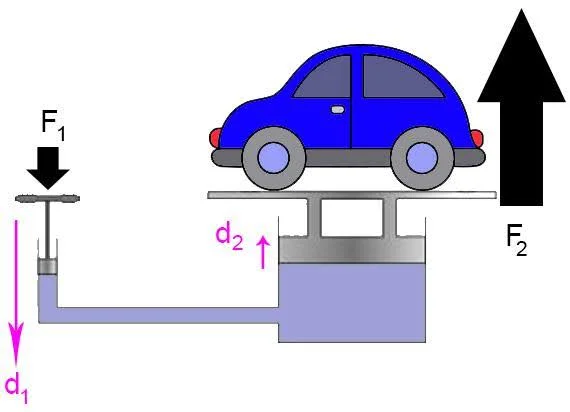
A hydraulic press has two cylinders topped by airtight pistons that can move up and down. The two cylinders are connected by a tube filled with an incompressible fluid. The force is applied on the narrow cylinder, and the load is placed on the broader cylinder.

Initially, no force is applied, so both pistons are at the same level. Therefore, the pressure is the same at all levels of the fluid, according to Pascal’s law.

Force \({{F_1}}\) is applied on the piston over the narrow cylinder with a cross-sectional area \({{A_1}}\) pushing it down the cylinder.

pressure, \({P_1} = \frac{{{F_1}}}{{{A_1}}}\)

The increased pressure due to the applied force spreads throughout the fluid. As a result, the fluid applies the same pressure on the movable piston of the broader cylinder with \({P_2}\).

According to Pascal’s law,

\({P_1} = {P_2}\)

\(\frac{{{F_1}}}{{{A_1}}} = \frac{{{F_2}}}{{{A_2}}}\)

We can write this as,

\(\frac{{{F_2}}}{{{F_1}}} = \frac{{{A_2}}}{{{A_1}}}\)

If \({A_2} \gg {A_1}\), then \({F_2} \gg {F_1}\)

There is no change in work. Work done is the same at both ends.

\({\rm{work}}\,{\rm{done = force}}\,{\rm{applied \times distance}}\,{\rm{moved}}\,{\rm{by}}\,{\rm{the}}\,{\rm{object}}\)
\({W_1} = {F_1} \times {d_1}\)
\({W_2} = {F_2} \times {d_2}\)
\({W_1} = {W_2}\)

This means that,

\(\frac{{{F_2}}}{{{F_1}}} = \frac{{{d_1}}}{{{d_2}}}\)

For example, if \({A_2} = 10{A_1}\), then \({F_2} = 10{F_1}\). Also, \({d_2} = \frac{1}{{10}}{d_1}\)

Suppose the broad cylinder has an area ten times the narrow cylinder. In that case, the force developed in the wide cylinder is ten times the force applied in the narrow end.

To move the load side piston up by one centimetre, the narrow side piston must be pushed down by ten centimetres.

Uses of hydraulic press

1. The hydraulic press is used to press metals in moulding, punching and crushing units.
2. Automobile workshops use hydraulic lifts to lift the vehicles up.
3. Pressing cotton bales into shape, crushing seeds for oil are some of the usages of a hydraulic press.zzzzzzzzzzzzzzzzzzzzz

Hydraulic Jack

It is similar to the hydraulic press but is smaller than it. We can press the smaller cylinder by pressing a foot pedal and raise cars for repairs or removing punctured tyres.

Hydraulic Brakes

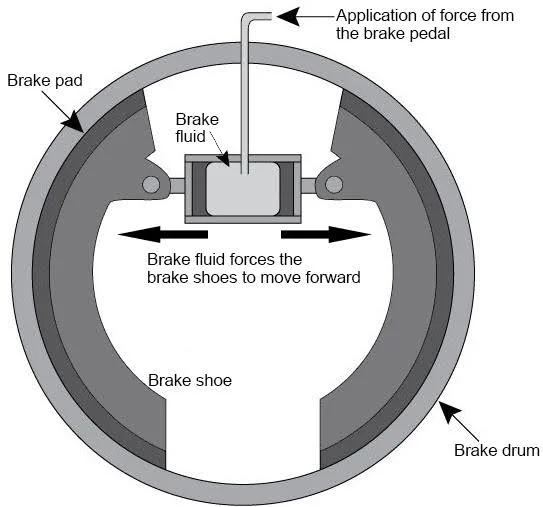
Four-wheelers use hydraulic braking systems. There is a chamber containing hydraulic fluid called the brake fluid. When we press the foot pedal of the brake, there is an increase in pressure. The brake fluid pressure moves the two brake shoes that make contact with the wheel and apply friction on it, thereby slowing it or stopping it.

Hydraulic systems are used in various industrial and aircraft systems to control the movement of different parts.

Pascal’s Law – Sample Problems

Q.1. A hydraulic press has two cylinders of areas \(100\;{\rm{c}}{{\rm{m}}^2}\) and \(500\;{\rm{c}}{{\rm{m}}^2}\). If a force of \(10\;{\rm{N}}\) is applied at the plunger, what force is created at the load end?
sol: Plunger side area, \({A_1} = 100\;{\rm{c}}{{\rm{m}}^2}\)
Load side area, \({A_2} = 500\;{\rm{c}}{{\rm{m}}^2}\)
Input force, \({F_1} = 10\;{\rm{N}}\)
\(\frac{{{F_2}}}{{{F_1}}} = \frac{{{A_2}}}{{{A_1}}}\)
\({F_2} = \frac{{{A_2}}}{{{A_1}}}{F_1}\)
\({F_2} = \frac{{500}}{{100}} \times 10 = 50\;{\rm{N}}\)

Force is multiplied five times when the output side area is five times the input side cylinder.

Q.2. A hydraulic press has cylinder areas in the ratio of \({\rm{10:1}}\). If the output side piston must move by \(10\;{\rm{cm}}\), what distance must the input side piston be pushed?
sol: \(\frac{{{F_2}}}{{{F_1}}} = \frac{{10}}{1}\)
\(\frac{{{F_2}}}{{{F_1}}} = \frac{{{d_1}}}{{{d_2}}}\)
Given, \({d_2} = 10\;{\rm{cm}}\)
\({d_1} = \frac{{{F_2}}}{{{F_1}}}{d_1}\)
\({d_1} = \frac{{10}}{1}10 = 100\;{\rm{cm}}\)
The input side piston must be pushed \(100\;{\rm{cm}}\) to make the output side piston move up by \(10\;{\rm{cm}}\).

Summary

Pascal’s law is the basis for many industrial and domestic applications. We have seen here a few such applications. Large objects are lifted easily with less effort. This is possible with the application of this law that gives the relation between the force applied and the surface area. The larger the surface area, the lesser is the force required. Hydraulic presses are used in crushing metals and scrap machinery, making cotton bales, and in vegetable oil extraction. Earthmoving equipment, car lifts, brakes of vehicles are just a few of the machines that use this law as a basis. A knowledge of this law is needed not just in the design of these devices but in all applications dealing with fluids, such as the design of dams, pipes carrying water, etc.

FAQs on Pascal’s Law

Let’s look at some of the commonly asked questions about Pascal’s law:

Q.1. Why does a balloon filled with water squirt it in all directions when we press it?
Ans: Pascal’s law states that pressure in all directions when we apply force at one point.

Q.2. In a hydraulic lift, does the load end move more distance than the narrow end?
Ans: No. The load end piston or the wider piston moves a smaller distance compared to the narrow cylinder piston.

Q.3. In a hydraulic press, is more work done?
Ans: No. Work done in pressing a smaller piston to move a larger piston are equal.

Q.4. What is the force in a piston whose area is double the plunger piston?
Ans: If the area of the load side piston is double the plunger piston (narrow side), the force is doubled.

Q.5. Does pressing the narrow end of a bottle filled with water burst the bottle?
Ans: Yes. The force creates a high pressure inside the bottle and may even burst the bottle if it goes above the tolerable level. It was demonstrated by Pascal in an experiment using what is now called Pascal’s barrel.

We hope you find this article on Pascal’s Law helpful. In case of any queries, you can reach back to us in the comments section, and we will try to solve them.