Patterns and Puzzles: Number Pattern, Maths Puzzles, Benefits and Examples

Patterns and Puzzles: Pattern in maths is a sequence or series that repeats. The sequence can be of any numbers, variables, or shapes. The pattern will be repeated based on certain rules that connect the terms in the series.

Another interesting concept in maths puzzles. They are an essential part of recreational mathematics. Math puzzles require mathematics and logic to solve them. They have several benefits for students, and it helps with reducing the anxiety. Let us learn about patterns and puzzles, their rules & types from this article with some examples. Read on to find more.

Learn Best Maths Tricks

Pattern in Maths

In Mathematics, a pattern is an arrangement of numbers, colours, or shapes such that a certain rule connects them. The pattern may be related to a type of object or event. The rules that connect them also help in solving the problem.

Example
In a sequence of \(3,6,9,12\), each number increases by \(3\).
Some of the numerical patterns are:
Even number pattern: \(2,4,6,8,10 \ldots\)
Odd number pattern: \(3,5,7,9,11 \ldots\)
Fibonacci number pattern: \(1,1,2,3,5,8,13 \ldots\)

Number Patterns

A set of numbers that observe a particular sequence are known as a number pattern. Patterns establish the relationship between two numbers in the sequence. To solve problems on number patterns, let us understand the rules being followed in the pattern.

Example
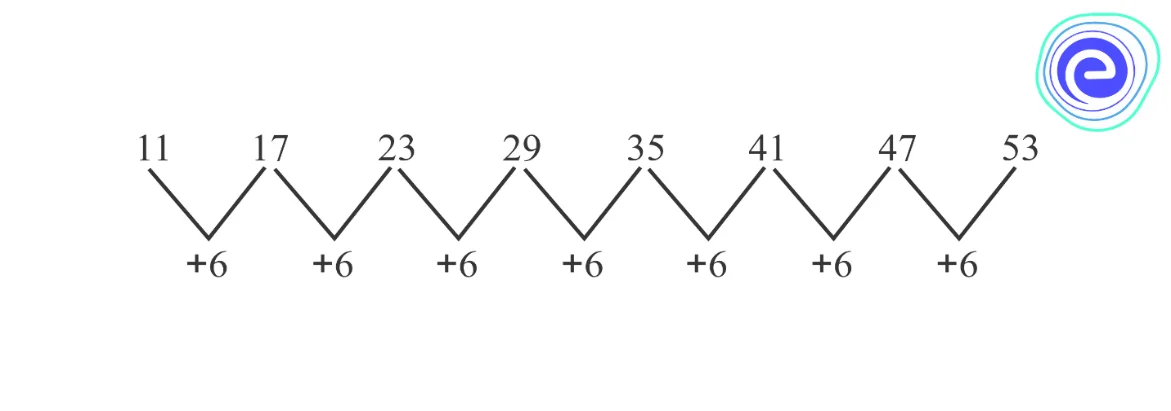
A sequence of numbers is \(11,17,23,29,35,41,47\), and \(53\). The figure below helps to recognize the relationship between the numbers.

We can observe the sequence is increased by \(6\). By adding \(6\) to the previous number, we get the successive numbers. Also, the difference between the two adjacent numbers is \(6\).

Rules for Pattern in Maths

To build the pattern, we must first comprehend the nature of the sequence as well as the distinction between two successive phrases. Certain guidelines must be followed in order to accomplish this. Let us know about these rules.

1. Finding missing terms: Consider the pattern \(1,4,9,16,25,36, \ldots..n\). Observing the pattern, we see that every number is the square of their position. Further terms can be found by squaring their positions.
2. Difference rule: We need to determine the differences between the terms in specific sequences. For instance, \(1,4,7,10,13 \ldots\) In such a pattern, the first step is to determine the difference between the adjacent terms. We can write down the remaining terms if we find the same difference. The difference between the terms is \(3\) in this case. By adding \(3\) to each previous term, the remaining terms can be found.

Types of Number Patterns

Types of number patterns are:
1. Arithmetic pattern
2. Geometric pattern
3. Fibonacci pattern

Arithmetic Pattern

The sequences are based on the addition and subtraction of terms in the arithmetic pattern. Another name for it is an algebraic pattern. Thus, we can use addition or subtraction to find the pattern by knowing two or more terms in a sequence.

For example: \(2,4,6,8,………12,14…………\),

Let us find the missing terms.

As we can observe the terms are increasing, we can use the addition process to find the missing terms

Add \(2\) to the previous terms in the pattern to obtain the next term.

First missing term: Add \(2\) to the previous term \((8)\), we get \(8+2=10\)

Second missing term: Add \(2\) to the previous term \((14)\), we get \(14+2=16\)

Thus the given arithmetic pattern is \(2,4,6,8,10,12,14,16\)

Geometric Pattern

Sequences based on the multiplication and division operations are defined as geometric patterns. If two or more numbers in a pattern are given, any missing terms can be found using multiplication and division operations.

For example: \(4,8, \ldots…., 32,64,……..256\).

We can observe that each term in sequence can be obtained by multiplying \(2\) with the previous term.

First missing term: Multiply \(2\) to the previous term \((8)\), we get \(8 \times 2=16\)

Second missing term: Multiply \(2\) to the previous term \((8)\), we get \(64 \times 2=128\)

Thus the given geometric pattern is \(4,8,16,32,64,128,256\)

Fibonacci Pattern

We obtain the next term in this sequence by adding the previous two terms starting with \(0\) and \(1\). This sequence is known as the Fibonacci pattern.

The Fibonacci pattern is given by \(0,1,, 1,2,3,5,8,13,21,34 \ldots\)

Puzzles Involving Number and Letter

The tricks involved in solving puzzles make us curious and increase our thinking. Puzzles were created to examine thinking ability and knowledge. There are various kinds of puzzles like crossword puzzles, letter for digits puzzles, etc.

In the letter for digits puzzle, we have to find which letter takes the place of digits in arithmetic sum and find out which letter represents which digit. It is like cracking a code. 

Rules for Solving Puzzles

The following are the two rules to be followed in solving a puzzle

1. Each letter represents only one digit in a puzzle, which means that one letter stands for one digit.
2. The first digit of any puzzle cannot be zero. For example, we write thirty-four as \(34\) and not \(034\).

Examples:

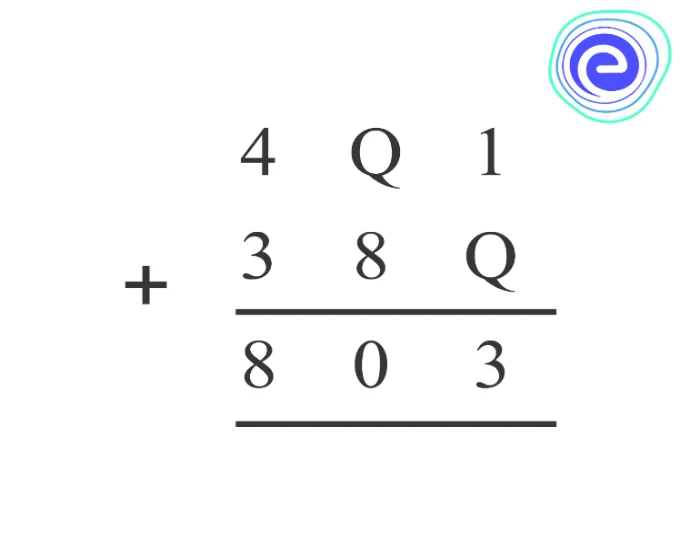
Find \(Q\) in the following:

Solution: In column one (starting from right), from \(Q+1\) we get \(3\) at the units place.

\(\Rightarrow Q+1=3\)

\(\Rightarrow Q=2\)

In the middle column, \(Q+8\) gives a number such that it has \(0\) at its units place. So \(Q=2\). Verification: When \(Q(2)\) is added to \(8\) it results in \(10\), and hence \(1\) is carried ahead. In the third column \(4+3+1\) (carry) \(=8\)

Benefits of Puzzles

In addition to having fun while solving a puzzle, there are several benefits. Below are a few surprising benefits of puzzle-solving.

1. Mental exercise: Puzzles help complete brain exercise that is left and right side. Both sides must communicate and work together as creativity, emotions, logical thinking, and objective are required to solve a puzzle
2. Better visual-spatial reasoning: We place the puzzles within larger images by seeing different pieces to assemble. This exercise improves spatial reasoning.
3. Greater attention to detail: When there is a similarity in the number of pieces, it becomes necessary to pay attention to details. You have to be conscious to find the small difference that will help you solve the puzzle. 
4. Improve memory: Keep in mind the numbers and try to find the connection from the remaining set of numbers. By this, you are increasing the mental speed and thoughts by strengthening the neural connections. Your short-term memory also increases.
5. Increase your IQ: The IQ of a student is improved by solving the puzzles.
6. Improve problem-solving ability: When the puzzles cannot be solved,  a student will take different approaches. Here learning of formulating theories, testing hypotheses, and changing of perspective takes place.
7. Increased productivity: When you are less stressed, it is easy to concentrate. When your concentration increases, your productivity also does increase.
8. Better mood: Puzzles help to increase memory, concentration, and motivation that encourages you to challenge yourselves.

Solved Examples on Puzzles and Patterns

Q.1. Determine the value of \(P\) and \(Q\) in the following pattern.
\(85,79,73,67,61,55,49,43, P, 31,25, Q\)
Ans: Given sequence: \(85,79,73,67,61,55,49,43, P, 31,25, Q\)
Here, the number is decreasing by \(6\).
The previous number of \(P\) is \(43\). So, \(P\) will be \(43-6, P=37\)
The previous number of \(Q\) is \(25\). So, \(Q\) will be \(25-6, Q=19\)
Therefore, the value of \(P\) is \(37\), and \(Q\) is \(19\).

Q.2. Determine the value of \(A\) and \(B\) in the following pattern.
\(15,22,29,36,43, A, 57,64,71,78,85, B\)
Ans: Given sequence: \(15,22,29,36,43, A, 57,64,71,78,85, B\)
Here, the number is increasing by \(+7\)
The previous number of \(A\) is \(43\). So, \(A\) will be \(43+7, A=50\)
The previous number of \(B\) is \(85\). So, \(B\) will be \(85+7, B=92\)
Therefore, the value of \(A=50\) and \(B=92\).

Q.3. Find the missing value in the geometric pattern: \(120,60, \ldots, 15\)
Ans: Given: Geometric pattern is \(120,60,15, \ldots\).
In this geometric pattern, the rule used is “Divide the previous term by \(2\) to get the next term”.
(i.e.,) \(\frac{120}{2}=60\)
Then, the first missing term \(=\frac{60}{2}=30\)
Second Missing term \(=\frac{15}{2}=7.5\)
Hence, the geometric sequence is \(120,60,30,15,7.5\).

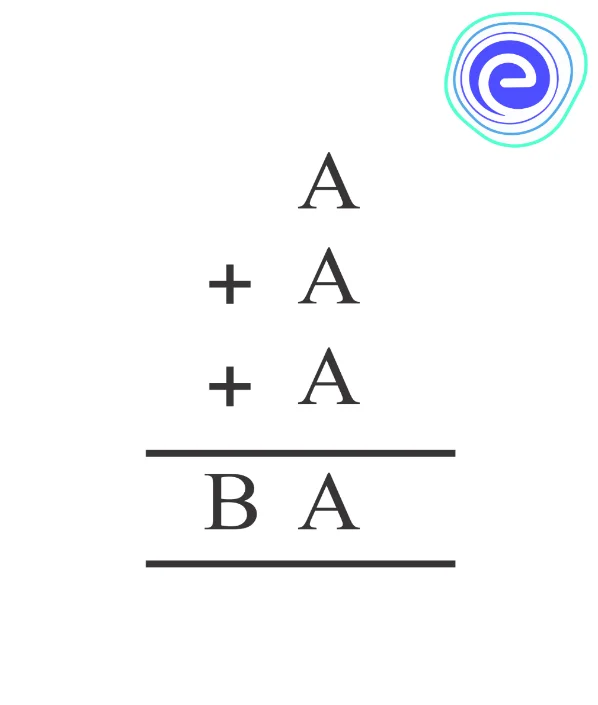
Q.4. Find the value of \(A\).

Ans: We have to find the value of \(A\) and \(B\). \(A\) is any number whose thrice sum with itself is also \(A\). Therefore, the sum of two \(A\)’s should be \(0\). This case is possible only for \(A=0\) or \(A=5\)
In this case, if \(A=0\), the entire sum will be \(0\) and hence \(B=0\).
But this is not possible as it will lead to \(A=B\)
We know that different letters represent different digits. Therefore we take the case in which \(A=5\)
Hence \(A+A+A=5+5+5=15\)
So we get \(B=1\).

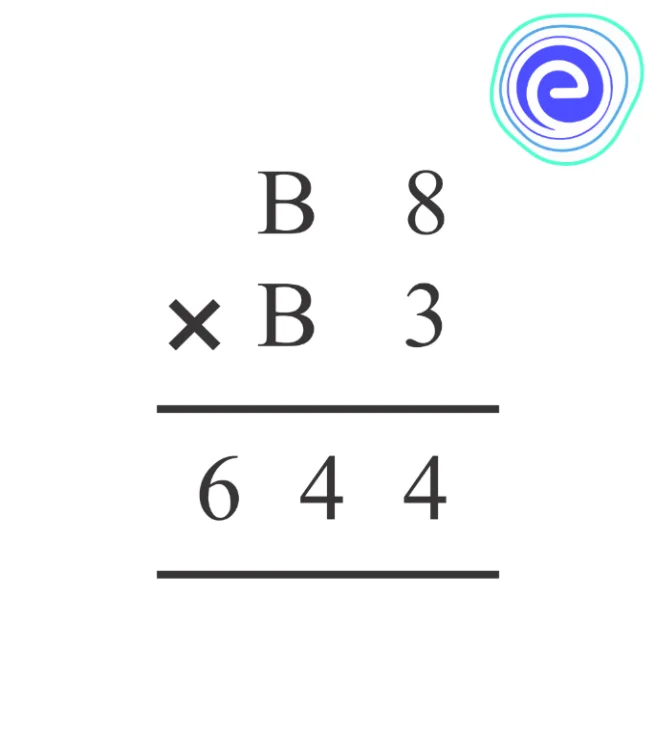
Q.5. Find the value of \(B\) in the following:

Ans: Let the numbers be \(10 B+8\) and \(10 B+3\). The product of these numbers will be \(644\).
\(\Rightarrow(10 B+8)(10 B+3)=644\)
\(\Rightarrow 100 B 2+110 B+24=644\)
\(\Rightarrow 100 B 2+110 B-620=0\)
\(\Rightarrow 10 B 2+11 B-62=0\)
\(\Rightarrow 10 B 2-20 B+31 B-62=0\)
\(\Rightarrow 10 B(B-2)+31(B-2)=0\)
\(\Rightarrow(B-2)(10 B+31)=0\)
\(\Rightarrow B=2\) or \(B=-3110\) (this value is discarded as \(B\) is an integer)
\(\Rightarrow B=2\)

Summary

In this article, we looked at the pattern and discovered the value of puzzle-solving. In math, we studied how the pattern is related. Numbers have a relationship that can be used to create patterns. We looked at number patterns, rules to follow, and different types of numbers.

Then we went on to another fascinating math topic that can help you relax. We concentrated on number and letter problems, puzzle principles, and the advantages of solving puzzles. We’ve solved examples to help students understand patterns and riddles better.

Learn About Types of Patterns

FAQs on Puzzles and Patterns

Q.1. How are puzzles related to math?
Ans: When a student is solving a puzzle, he/she explores what information matters, how to break down the puzzle into smaller steps, and the reasons for certain strategies over others. All these are related to maths skills.

Q.2. Is there mathematics involved in patterns?
Ans: Mathematics itself is a study of patterns. Studying patterns is the chance to create, discover, observe and experiment. By learning the rules based on the data we gather, predicting what comes next, and checking if the same pattern occurs when variables are changed.

Q.3. How are patterns connected to mathematics?
Ans: Using patterns to analyze and solve problems is an extremely powerful tool for mathematics. Students who analyze the patterns to solve problems can also understand new concepts.

Q.4. Why are patterns important in mathematics and real life?
Ans: Patterns are the heart of math. The ability to recognize and create patterns help us make predictions based on our observations; this is an important math skill. We use patterns to represent identified regularities and to form generalizations. 

Q.5. How many types of patterns are there in Mathematics?
Ans: Some of the different types of patterns in Mathematics are:
1. Arithmetic Sequence
2. Geometric Sequence
3. Square Numbers
4. Cube Numbers
5. Triangular Numbers
6. Fibonacci Numbers

Q.6. What is a pattern, with example?
Ans: A list of numbers that follow a certain sequence or pattern. Example:
\(1,4,7,10,13,16, \ldots\) starts at \(1\) and jumps \(3\) every time. Another Example:
\(2,4,8,16,32, \ldots\) doubles each time.

We hope this detailed article on patterns and puzzles helped you in your studies. If you have any doubts, queries or suggestions regarding this article, feel to ask us in the comment section and we will be more than happy to assist you. Happy learning!