Permutations when All the Objects are Distinct: Assume you own a suitcase with a number lock. The number lock has four wheels, and each is labelled with ten digits ranging from \(0\) to \(9\). The lock can be opened by arranging four specific digits in a specific sequence with no repetition. You must have forgotten this particular sequence of digits. You only remember the first digit, which is \(7\).

How many \(3\) -digit sequences may you have to check in order to open the lock? To respond to this question, you may immediately begin listing all possible arrangements of the remaining \(9\) digits, three at a time. However, this method will be time-consuming due to a large number of possible sequences. We can solve this if we know the permutations that are possible with the three digits.

LEARN EXAM CONCEPTS ON EMBIBE

What are Permutations?

To find the number of \(4\) letter words, which can be formed out of the letters \(R, O, S, E\), with or without any meaning, where the repetition of the letters is not allowed.

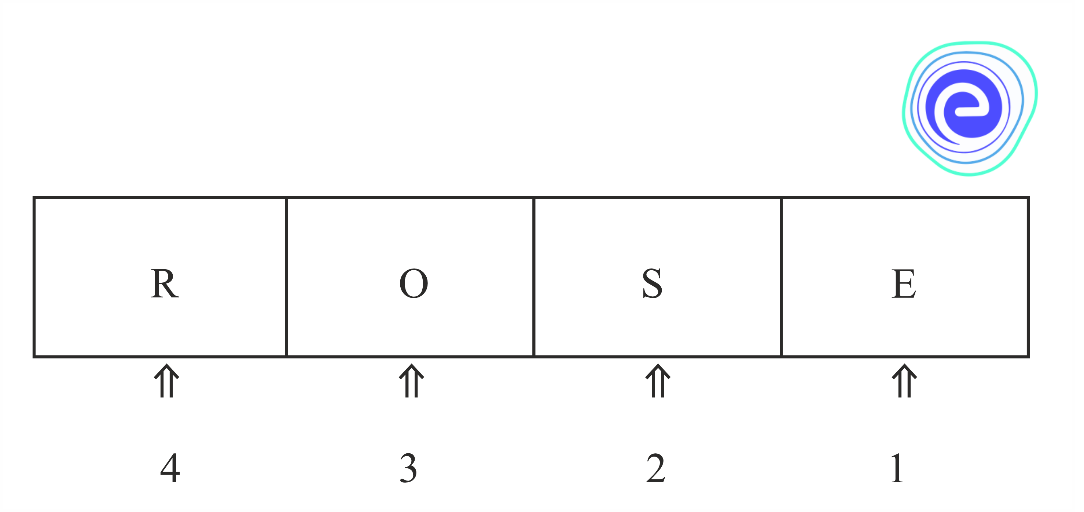
There are as many \(4\) letter words as there are ways of filling in \(4\) empty places by the \(4\) letters where repetition is avoided.

• The first place is filled in \(4\) different ways by the \(4\) letters \(R, O, S, E\).
• The second place is filled by any one of the remaining \(3\) letters in \(3\) distinct ways.
• The third place is filled in \(2\) different ways.
• The fourth place is filled only in \(1\) way.

Thus, the number of different ways in which the \(4\) places can be filled by the fundamental multiplication principle is \(4 \times 3 \times 2 \times 1=24\). Hence, the total number of possible words is \(24\) .

Here, we count the different possible arrangements of the letters, such as \(R O S E, R E O S, \ldots\). Each arrangement in the list is different from the other. We can say that the order of writing the letters is important. Each arrangement in this ordered way is called a permutation of \(4\) different distinct letters taken all at a time.

Now, if we have to find the number of \(3\)-letter words, which can be formed out of the letters of the word NUMBER, with or without meaning, where the repetition of the letters is not allowed. Here, we have to count the arrangements like \(N U M, N M U, M U N, N U B, \ldots\), etc.
Here, we count the permutations of \(6\) different distinct letters taken \(3\) at a time.
By using the multiplication principle, the required number of words \(=6 \times 5 \times 4=120\). If the repetition of the letters is allowed, the required number of words will be \(6 \times 6 \times 6=216\)

Hence, we can state that a permutation is an arrangement in a definite order of a number of distinct objects taken, some or all at a time.

Formula for \({ }^{n} P_{r}\)

\({ }^{n} P_{r}=\frac{n !}{(n-r) !}\) \(0 \leq r \leq n\)

we saw that

\({ }^{n} P_{r}=n(n-1)(n-2) \ldots(n-r+1)\)

Multiplying the numerator and denominator by \((n-r)(n-r-1) \ldots 3 \times 2 \times 1\) we get \(^n{P_r} = \frac{{n(n – 1)(n – 2) \ldots (n – r + 1)(n – r)(n – r – 1) \ldots 3 \times 2 \times 1}}{{(n – r)(n – r – 1) \ldots 3 \times 2 \times 1}} = \frac{{n!}}{{(n – r)!}}\)

This is a more convenient expression for \({ }^{n} P_{r}\) than the previous one.

In particular, when \(r=n,{ }^{n} P_{n}=\frac{n !}{(n-n) !}=\frac{n !}{0 !}=\frac{n !}{1}=n !\)

Counting the permutations is simply counting the number of ways in which some or all objects are rearranged at the same time. Arranging no objects at all is the same as leaving all of the objects behind, and we know there is only one way to do so. Consequently, we can have

\({ }^{n} P_{0}=\frac{n !}{(n-0) !}=\frac{n !}{n !}=1\)

Therefore, the formula is applicable for \(r=0\) also. Thus,

\({ }^{n} P_{r}=\frac{n !}{(n-r) !}, \quad 0 \leq r \leq n\)

PRACTICE EXAM QUESTIONS AT EMBIBE

Permutations when All the Objects are Distinct

The number of permutations of \(n\) different objects taken \(r\) at a time, where \(0<r \leq n\) and the objects do not repeat is \(n(n-1)(n-2) \ldots(n-r+1)\), which is denoted by \({ }^{n} P_{r}\).

Proof:

There will be as many permutations as there are ways of filling in \(r\) vacant places by the \(n\) objects. The first place can be filled in \(n\) ways; following which the second place can be filled in \((n-1)\) ways, the third place can be filled in \((n-2)\) ways,.., the \(r^{\text {th }}\) place can be filled in \((n-(r-1))\) ways.

Hence, the number of ways of filling in \(r\) vacant places in succession is given by

\(n(n-1)(n-2) \ldots(n-(r-1))\) or \(n(n-1)(n-2) \ldots(n-r+1)\)

This expression for \({ }^{n} P_{r}\) is cumbersome, and we need a notation that will help to reduce the size of this expression. The symbol \(n\) ! (read as factorial \(n\) or \(n\) factorial) comes into play.

Steps to Calculate Permutations of Distinct Objects

Following are the steps to calculate the permutations

Step 1: Determine the number of options available for the first situation.

Step 2: Determine how many options are still available in the second situation.

Step 3: Continue until all of the available spots are filled.

Step 4: Multiply the number of options obtained so far together.

Permutations when All the Objects are Distinct When Repetition is Allowed

The number of permutations of \(n\) different objects taken \(r\) at a time, where repetition is allowed, is \(n^{r}\).

The number of different \(3\) -letter words that can be formed by the letters of the word \(N U M B E R\) is calculated as

\({ }^{6} P_{3}=\frac{6 !}{(6-3) !}\)

\(=\frac{6 !}{3 !}\)

\(=\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{3 \times 2 \times 1}\)

\(=4 \times 5 \times 6\)

\(\therefore{ }^{6} P_{3}=120\)

Here, repetition is not allowed in this case.

If the repetition is allowed for the same case, then for each of the three vacant spaces, we can insert any of the \(6\) letters in the word \(NUMBER\).

Hence, the first position can have any of the \(6\) letters, the second position can have any of the \(6\) letters and the third position also can have any of the \(6\) letters.

Hence, the required number of words would be \(6 \times 6 \times 6=6^{3}=216\).

Solved Examples – Permutations when All the Objects are Distinct

Below are a few solved examples that can help in getting a better idea.

Q1. How many \(4\) -digit numbers can be formed by using the digits \(1\) to \(9\) if repetition of digits is not allowed?
Sol: The required \(4\) digit numbers \(={ }^{9} P_{4}=\frac{9 !}{(9-4) !}\)
\(=\frac{9 !}{5 !}\)
\(=\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times 1}\)
\(=9 \times 8 \times 7 \times 6=3024\)

Q.2. How many distinct words can be made up by using all of the letters in the word ‘TRIANGLES’?
Sol: There are \(9\) distinct letters in the word TRIANGLE. Thus, the number of different permutations of the letters of this word is,
\({ }^{9} P_{9}=\frac{9 !}{(9-9) !}\)
\(=\frac{9 !}{0 !}\)
\(=\frac{9 !}{1}\)
\(=9 !\)
Hence, the number of words is \(9!\)

Q.3. How many \(3\)-letter words can be made using the letters of the word ‘TRAPEZIUMS’, with or without meaning, if repetition of letters is not allowed?
Sol: The word ‘TRAPEZIUMS’ has \(10\) different letters. So, the number of \(3\) letter words (with or without meaning) formed by using these letters
\({ }^{10} P_{3}=\frac{10 !}{(10-3) !}=\frac{10 !}{7 !}\)
\(=\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}\)
\(=10 \times 9 \times 8\)
\(=720\)

Q.4. How many words that start with \(T\) and end with \(L\) can be made from the word TRIANGLES?
Sol: If we fix \(T\) at the start and \(L\) at the end of the word, those two spaces are not to be considered further. We just have to permute \(7\) distinct letters in \(7\) places.
\({ }^{7} P_{7}=\frac{7 !}{(7-7) !}\)
\(=\frac{7 !}{0 !}\)
\(=\frac{7 !}{1}\)
\(=7 !\)
Hence, the number of words is \(7 !\)

Q5. In a sports company, the manager must select the top three goals of the month, from a list of ten goals. Find out in how many ways can the top three goals be decided?
Sol: Since the manager must decide the top three goals of the month; the order of the goals is very important! Thus, the problem is of permutations.
When he pick up three goals from a list of ten:
Possible Permutations \(={ }^{10} P_{3}=10 !(10-3) !=10 \times 9 \times 8=720\)
Hence, there are \(720\) ways of picking the top three goals!

Summary

The number of permutations of \(n\) different things taken \(r\) at a time, where repetition is not allowed, is denoted by \(^n{P_r}\) and is given by \({ }^{n} P_{r}=\frac{n !}{(n-r) !}, 0 \leq r \leq n\). And \(n!\) is read as \(n\) factorial, and it is equal to \(n !=1 \times 2 \times 3 \times \ldots \times n\), which can also be stated as \(n! = n \times (n – 1)!\) The number of permutations of \(n\) different things, taken \(r\) at a time, where repetition is allowed, is \(n^{r}\). To calculate the permutations of distinct objects, first determine the number of options available for the first situation. Then, determine how many options are still available in the second situation. Continue until all available spots are filled and multiply the number of options obtained so far together.

FAQs on Permutations when All the Objects are Distinct

Students might be having many questions with respect to the Permutations when All the Objects are Distinct. Here are a few commonly asked questions and answers.

Q.1. What is the permutation of distinct objects?
Ans: A permutation is an arrangement in a definite order of a number of distinct objects taken, some or all at a time.

Q.2. What is the formula for the permutation of a set of distinct objects?
Ans: The number of permutations of \(n\) different things taken \(r\) at a time, where repetition is not allowed, is denoted by \({ }^{n} P_{r}\) and is given by
\({ }^{n} P_{r}=\frac{n !}{(n-r) !}, 0 \leq r \leq n\)

Q.3. Are permutations and combinations different?
Ans: Permutation is arranging all the members in order, while the combination is the selection of elements from a collection.

Q.4. What is the formula for permutation of a set of distinct objects when repetition is allowed?
Ans: The number of permutations of \(n\) different things, taken \(r\) at a time, where repetition is allowed, is \(n^{r}\).

Q.5. What does \(n!\) denote?
Ans: The factorial of a number is the function that multiplies the number by every natural number below it. \(n!\) is read as \(n\) factorial, equal to \(n !=1 \times 2 \times 3 \times \ldots \times n\), which can also be stated as \(n !=n \times(n-1) !\).

ATTEMPT MOCK TESTS ON EMBIBE

We hope this information about the Permutations when All the Objects are Distinct has been helpful. If you have any doubts, comment in the section below, and we will get back to you soon.