Permutations When All the Objects Are Not Distinct Objects: Definition, Formulas

Permutations when all the objects are not distinct objects: A permutation is an arrangement in a specific order of several objects taken, some or all, at a time. The number of permutations of \(n\) different objects taken \(r\) at a time, where \(0 < r \le n\) and the objects do not repeat is \(n(n – 1)(n – 2) \ldots (n – r + 1)\). It is denoted by \(^n{P_r}\) .

The number of permutations of \(n\) different objects taken \(r\) at a time, where repetition is allowed, is \({n^r}\). In all these cases, we consider the objects involved in the permutation are all distinct objects. But there can be cases where all the objects are not distinct. Let us learn about such cases in this article.

Permutations

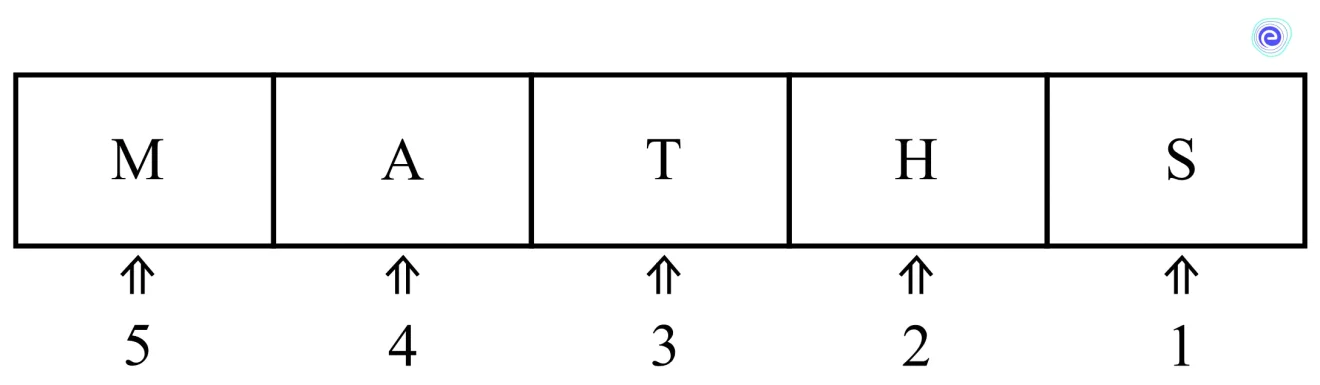
Let us see an example of the number of \(5\) letter words, which can be formed out of the letters \(M, A, T, H, S\) with, or without, meaning, where repetition of letters is not allowed.

There are as many \(5\) letter words as there are ways of filling in \(5\) empty places by the \(5\) letters with repetition is avoided.

• The first vacant place can be filled in \(5\) different ways by any one of the \(5\) letters \(M, A, T, H, S\).
• The second place is filled in by any one of the remaining \(4\) letters in \(4\) different distinct ways.
• The third vacant place can be filled in \(3\) different ways.
• The fourth place can be filled in \(2\) ways, and the fifth position with only in \(1\) way.

By the fundamental multiplication principle, the different number of ways in which the\(5\) places can be filled \( = 5 \times 4 \times 3 \times 2 \times 1\).

So, the required number of words is \(120\).

Here, we count the different possible arrangements of the letters such as \(MATHS, MATSH, MASTH…\) etc., where each arrangement is different from the other.

Each arrangement in such an ordered way is called a permutation of \(5\) distinct letters taken all at a time.

Now, if we have to find the number of \(4\)-letter words, which can be formed out of the letters of the word COUNTERS, with or without meaning, where the repetition of the letters is not allowed. Now, we have to count the arrangements like \(CONT, ONTE,TERS….\) etc.

Here, we count the permutations of \(8\) different distinct letters taken \(4\) at a time.

By using the multiplication principle, the required number of \( = 8 \times 7 \times 6 \times 5 = 1680\).

If the repetition of the letters is allowed, the required number of words will be \(8 \times 8 \times 8 \times 8 = 4096\)

Hence, we can state that a permutation is an arrangement in a definite order of several distinct objects taken, some or all at a time.

Permutations when All the Objects are Distinct

The number of permutations of \(n\) different objects taken \(r\) at a time, where \(0 < r \le n\) and the objects do not repeat is \(n(n – 1)(n – 2) \ldots (n – r + 1)\) which is denoted by \(^n{P_r}\).

\(^n{P_r} = \frac{{n!}}{{(n – r)!}},\quad 0 \le r \le n\)

In particular, when \(r = n{,^n}{P_n} = \frac{{n!}}{{(n – n)!}} = \frac{{n!}}{{0!}} = \frac{{n!}}{1} = n!\)

Counting the permutations is simply counting the number of ways in which some or all objects are rearranged simultaneously. Arranging no objects at all is the same as leaving all of the objects behind, and we know there is only one way to do so. Consequently, we can have \(^n{P_0} = \frac{{n!}}{{(n – 0)!}} = \frac{{n!}}{{n!}} = 1\)

The number of permutations of \(n\) different distinct objects taken \(r\) at a time, where repetition is allowed, is  \({n^r}\).

Permutations when Some Objects are Repeated

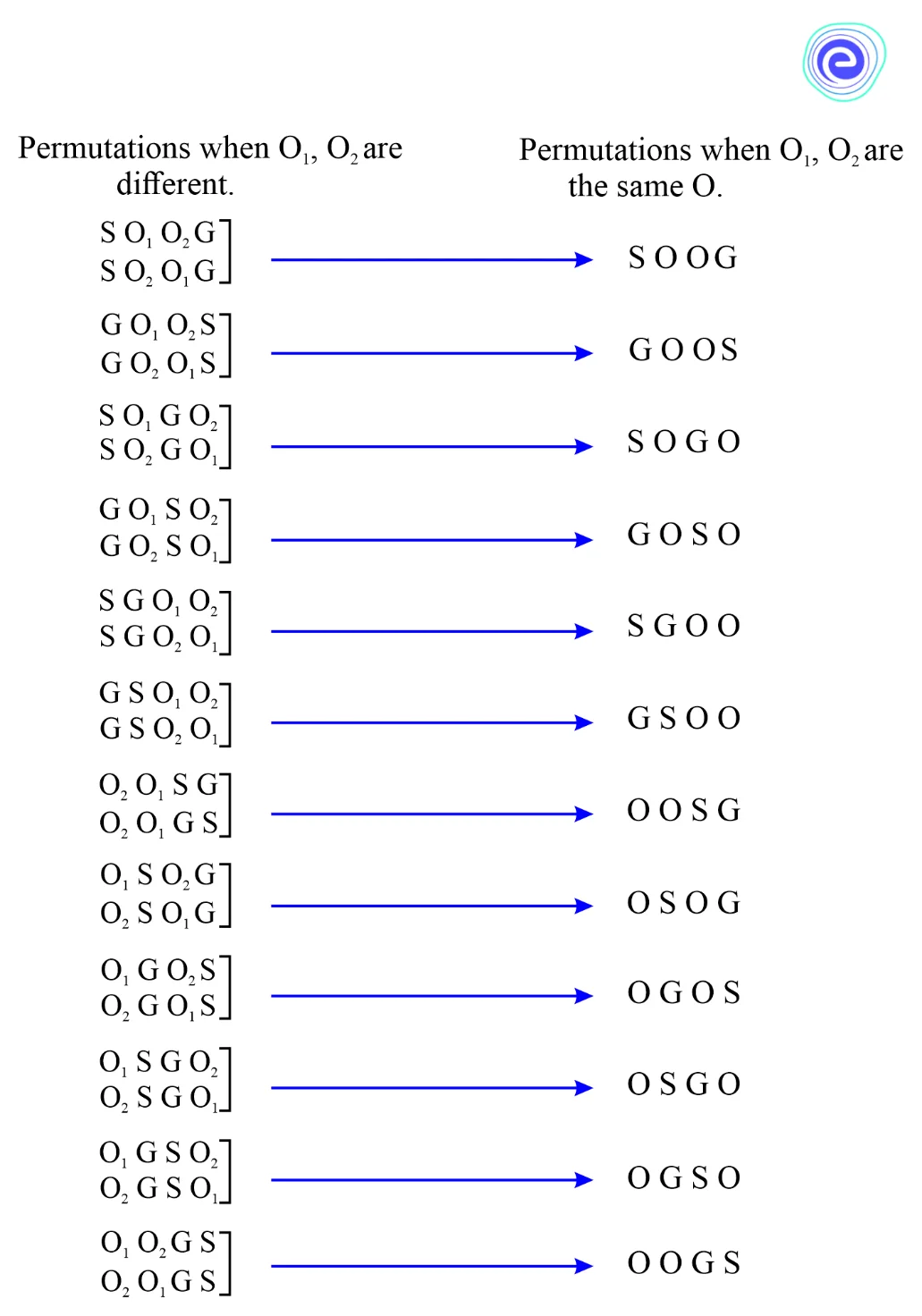
Suppose we need to find the number of ways of rearranging the letters of the word \(GOOS\). Here, the letters of the word are not all different. There are \(2 Os\), which are of the same kind. Let us treat, temporarily, the \(2 Os\) as different, say, \({O_1}\) and \({O_2}\). The number of permutations of \(4\)-different letters, taken all at a time, is \(4!\). 

Consider one of these permutations, say, \(G{O_1}{O_2}S\). Corresponding to this, we have \(2!\) permutations \(G{O_1}{O_2}S\) and \(G{O_2}{O_1}S\) which will be the same permutation if \({O_1}\) and \({O_2}\) are not considered as different, i.e., if \({O_1}\) and \({O_2}\) are the same \(O\) at both places. Therefore, the required number of permutations \( = \frac{{4!}}{{2!}} = 3 \times 4 = 12\)

In general, the number of permutations of \(n\) objects, where \(p\) objects are of the same kind, and the rest is all different, is given by \(\frac{{n!}}{{p!}}\).

Let us now see the number of ways of rearranging the letters of the word \(INSTITUTE\). Here, there are \(9\) letters, in which \(I\) appears \(2\) times and \(T\) appears \(3\) times.

Consider these letters different and name them as \({I_1},{I_2},{T_1},{T_2},{T_3}\). The number of permutations of the \(9\) different letters, taken all at once, is \(9!\) Consider one such permutation, say,\({I_1}N{T_1}S{I_2}{T_2}UE{T_3}\) .

Here if \({I_1},{I_2}\) are not the same and \({T_1},{T_2},{T_3}\) are not the same, then \({I_1},{I_2}\) can be arranged in \(2!\) ways and \({T_1},{T_2},{T_3}\) can be arranged in \(3!\) ways. Therefore, \(2! \times 3!\) permutations will be just the same permutation corresponding to this chosen permutation \({I_1}N{T_1}S{I_2}{T_2}UE{T_3}\).

Hence, the total possible number of different permutations \( = \frac{{9!}}{{2!3!}}\).

So, we can say, in general, the number of permutations of \(n\) objects, where \({p_1}\) objects are of one kind, \({p_2}\) are of the second kind, …, \({p_k}\) are of \({k^{th}}\) kind and the rest, if anything left, are of a different kind is given by \(\frac{{n!}}{{{p_1}!{p_2}! \ldots \ldots {p_k}!}}\)

Solved Examples – Permutations when All the Objects are Not Distinct Objects

Below are a few solved examples that can help in getting a better idea.

Q.1. Find the number of possible permutations of the letters of the word \(ALLAHABAD\).
Ans: Here, there are \(9\) letters, of which there are \(4A’s,2L’s\) and the rest are all different.

Therefore, the required number of arrangements \( = \frac{{9!}}{{4!2!}}\)

\( = \frac{{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{4 \times 3 \times 2 \times 1 \times 2 \times 1}}\)

\( = \frac{{5 \times 6 \times 7 \times 8 \times 9}}{2}\)

\(=7560\)

Q.2. In how many ways can we arrange \(4\) red, \(3\) yellow and \(2\) green balls in a row if the balls of the same colour are congruent?
Ans:  Total number of discs are \(4 + 3 + 2 = 9\).

Out of \(9\) balls, \(4\) are red, \(3\) are yellow, and \(2\) green.

Therefore, the number of arrangements \( = \frac{{9!}}{{4!3!2!}}\)

\( = \frac{{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{(4 \times 3 \times 2 \times 1)(3 \times 2 \times 1)(2 \times 1)}}\)

\(=1260\)

Q.3. In how many different ways, the letters of the word \(‘PERMUTATIONS’\) can be arranged if the vowels are all together.
Ans: There are \(5\) vowels in the word: \(1E,1U,1A,1I,\) and \(1O\).
Since these vowels are occurring together, so consider them as one letter, and when this letter is combined with the remaining \(7\) letters, then we have \(8\) letters in all, which can be arranged in \(2! 8!\) ways.
Corresponding to the arrangements, the\(5\) vowels can be arranged in \(5!\) ways.

Hence, required no. of ways \( = \frac{{8!}}{{2!}} \times 5!\)

\( = 20160 \times 5!\)

\( = 24,19,200\)

Q.4. In how many of the distinct permutations of the letters in \(MISSISSIPPI\) do the four \(I’s\) not come together?
Ans: The word \(MISSISSIPPI\) has one \(M\), four \(I’s\), four \(S’s\), two \(P’s\) and a total of \(11\) letters.

The number of all types of permutations possible with the given letters.

\( = \frac{{11!}}{{4!4!2!}}\)

\( = \frac{{11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{4 \times 3 \times 2 \times 1 \times 4 \times 3 \times 2 \times 1 \times 2 \times 1}}\)

\( = \frac{{11 \times 10 \times 9 \times 7 \times 5}}{1}\)

\(=34650\)

Let us now find the case when all the \(I’s\) together and take it as one packet or unit. So now we have one \(M\), one unit of four \(I’s\), four \(S’s\), two \(P’s\) and a total of \(8\) units.

Therefore the number of permutations possible when all the \(I’s\) is together

\( = \frac{{8!}}{{4!2!}}\)

\(=84\)

Hence, the number of permutations of the distinct letters of the word \(MISSISSIPPI\) when four \(I’s\) do not come together \( = 34650 – 840\)

\(=33810\)

Q.5. Find the total number of words, with or without meaning, that can be formed with the letters of the word \(‘COCONUT’\).
Ans: The word \(‘COCONUT’\) contains \(7\) letters, and \(‘C\,\&\,O’\) occurs twice.

The number of permutations of \(n\) objects, where \({p_1}\) objects are of one kind, \({p_2}\) are of the second kind, …, \({p_k}\) are of \({k^{th}}\) kind and the rest, if anything left, are of a different kind is given by \(\frac{{n!}}{{{p_1}!{p_2}! \ldots \ldots {p_k}!}}\)

Hence, the number of words that can be formed by \({\rm{COCONUT}} = \frac{{7!}}{{2!2!}}\)

\( = \frac{{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{2 \times 1 \times 2 \times 1}}\)

\(=1260\)

Summary

Permutation determines the number of possible arrangements in a set when the order of the objects matters. It can be classified into three categories: Permutation of \(n\) distinct objects when repetition is not allowed; Permutation of \(n\) distinct objects when repetition is allowed, and permutation when the objects are not distinct.

The number of permutations of \(n\) objects, where \(p\) objects are of the same kind, and the rest is all different, is given by \(\frac{{n!}}{{p!}}\). The number of permutations of \(n\) objects, where \({p_1}\) objects are of one kind, \({p_2}\) are of the second kind, …, \({p_k}\) are of \({k^{th}}\) kind and the rest, if anything left, are of a different kind is given by \(\frac{{n!}}{{{p_1}!{p_2}! \ldots {p_k}!}}\).

FAQs on Permutations When All the Objects Are Not Distinct Objects

Students might be having many questions with respect to the Permutations when All the Objects are Not Distinct Objects. Here are a few commonly asked questions and answers.

Q.1. What is permutation?
Ans: A permutation is a technique that determines the number of possible arrangements in a set when the order of the arrangements matters.

Q.2. What is a permutation of a set of \(n\) distinct objects?  
Ans: The number of permutations of \(n\) different distinct objects taken \(r\) at a time, where \(0 < r \le n\) and the objects do not repeat, is denoted by \(^n{P_r}\) and given by \(^n{P_r} = \frac{{n!}}{{(n – r)!}}\)

Q.3. Are repetitions allowed when doing permutations?
Ans: Yes, repetitions are allowed in permutations. The number of permutations of \(n\) different distinct objects taken \(r\) at a time, where repetition is allowed, is \({n^r}\).

Q.4. What is the permutation of non-distinct objects?
Ans: The number of permutations of \(n\) objects, where \(p\) objects are of the same kind and the rest is all different, is given by \(\frac{{n!}}{{p!}}\). The number of permutations of \(n\) objects, where \({p_1}\) objects are of one kind, \({p_2}\) are of the second kind, …,\({p_k}\) are of \({k^{th}}\) kind and the rest, if anything left, are of a different kind is given by \(\frac{{n!}}{{{p_1}!{p_2}! \ldots \ldots {p_k}!}}\) .

Q.5. What are the types of permutations?
Ans: Permutation can be classified into three categories: Permutation of \(n\) distinct objects when repetition is not allowed; Permutation of \(n\) distinct objects when repetition is allowed and permutation when the objects are not distinct.

We hope this information about the Permutations when All the Objects are Not Distinct Objects has been helpful. If you have any doubts, comment in the section below, and we will get back to you.