Pressure Inside a Fluid: Meaning, Formula, Derivation, Examples

Pressure Inside a Fluid: We have all read about the three states of matter: Solids, liquids, and gases. Liquids and gases can flow, and that’s why these are together called fluids. Solids have a definite shape, size, and volume, but fluids do not have a definite shape. However, liquids have a definite volume, while gases take up the volume of the container. When a solid, for example, a ball, is kept on a table, it applies force on the table equal to its weight.

Similarly, fluids apply forces on the objects around them while we do not realise the force applied by the air around us unless strong winds start blowing; the force of liquids can be felt when we go swimming. We have to exert a good amount of force to swim properly across the pool. We know that when a force acts on a surface, pressure is involved. The pressure within a fluid is different from the pressure at its surface. Let us learn in detail about the pressure within a fluid.

What is Pressure?

Learn All Concepts on Fluid Mechanics

The pressure acting on a body is defined as the force per unit area that acts perpendicular to the body’s surface. It is a scalar quantity. When a force of magnitude \(F\) acting normally on a piston of area \(A,\) then the average pressure will be equal to the normal force acting per unit area on its surface. Mathematically, 

\({P_{av}} = \frac{F}{A}\)

The dimensions of pressure are: \(\left[ {{M^1}{L^{ – 1}}{T^{ – 2}}} \right]\)

The SI unit of pressure is Newton per metre square or \({\rm{N}}{{\rm{m}}^{{\rm{ – 2}}}}{\rm{.}}\) This is known as Pascal or \({\rm{Pa}}.\) It is named after the scientist Blaise Pascal. Another important unit of pressure is the atmospheric pressure. It is the pressure exerted by the atmosphere at sea level, i.e., \(1\;{\rm{atm}} = 1.013 \times {10^5}\;{\rm{Pa}}\)

Pressure Inside a Fluid

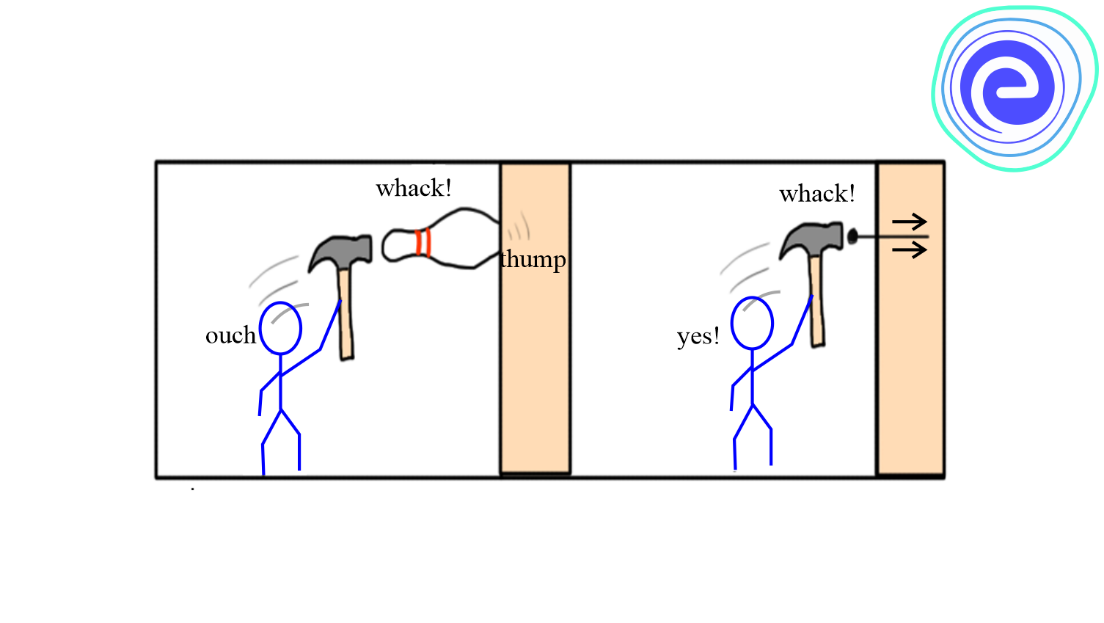
Fluid, at rest, exerts a force on the surface of an object submerged in it. The force applied by a fluid always acts normal to the surface of the object. If the fluid applies a force parallel to the surface of an object, then according to newton’s third law of motion, the object will exert an equal and opposite force parallel to the surface of the fluid. The force acting parallel to the fluid will cause the fluid to flow parallel to the surface, and, thus,  the fluid will not remain stationary, but this is not possible. Hence, the force applied by a fluid at rest always acts perpendicular to the object’s surface in contact with the fluid.

Pressure can be measured using a device shown below:

It is an idealised set-up consisting of an evacuated chamber with a spring attached to a piston. The spring is calibrated to measure the force acting on the piston. The inwards force experienced by the piston due to the fluid is balanced by the outward force exerted by the spring. Thus, the calibration on the spring will give an estimate of the force acting on it.

Liquids are mostly incompressible, and hence their density is almost constant at different pressures and hence we use the density of fluids to describe them. For a fluid of mass \(m\) and volume \(V\), the density can be given as:

\(\rho = \frac{m}{V}\)

It is a scalar quantity. The dimensions of density are \(\left[ {{M^1}{L^{ – 3}}{T^0}} \right]\) while its SI unit is \({\rm{kg}}\,{{\rm{m}}^{ – 3}}.\) The density of water is maximum at \({{\rm{4}}^{\rm{o}}}{\rm{C,}}\) and it’s equal to \(1.0 \times {10^3}\;{\rm{kg}}/{{\rm{m}}^3}.\) The relative density of a substance can be defined as the ratio of the density of a substance to the density of water at \({{\rm{4}}^{\rm{o}}}{\rm{C}}{\rm{.}}\) It is a dimensionless quantity.

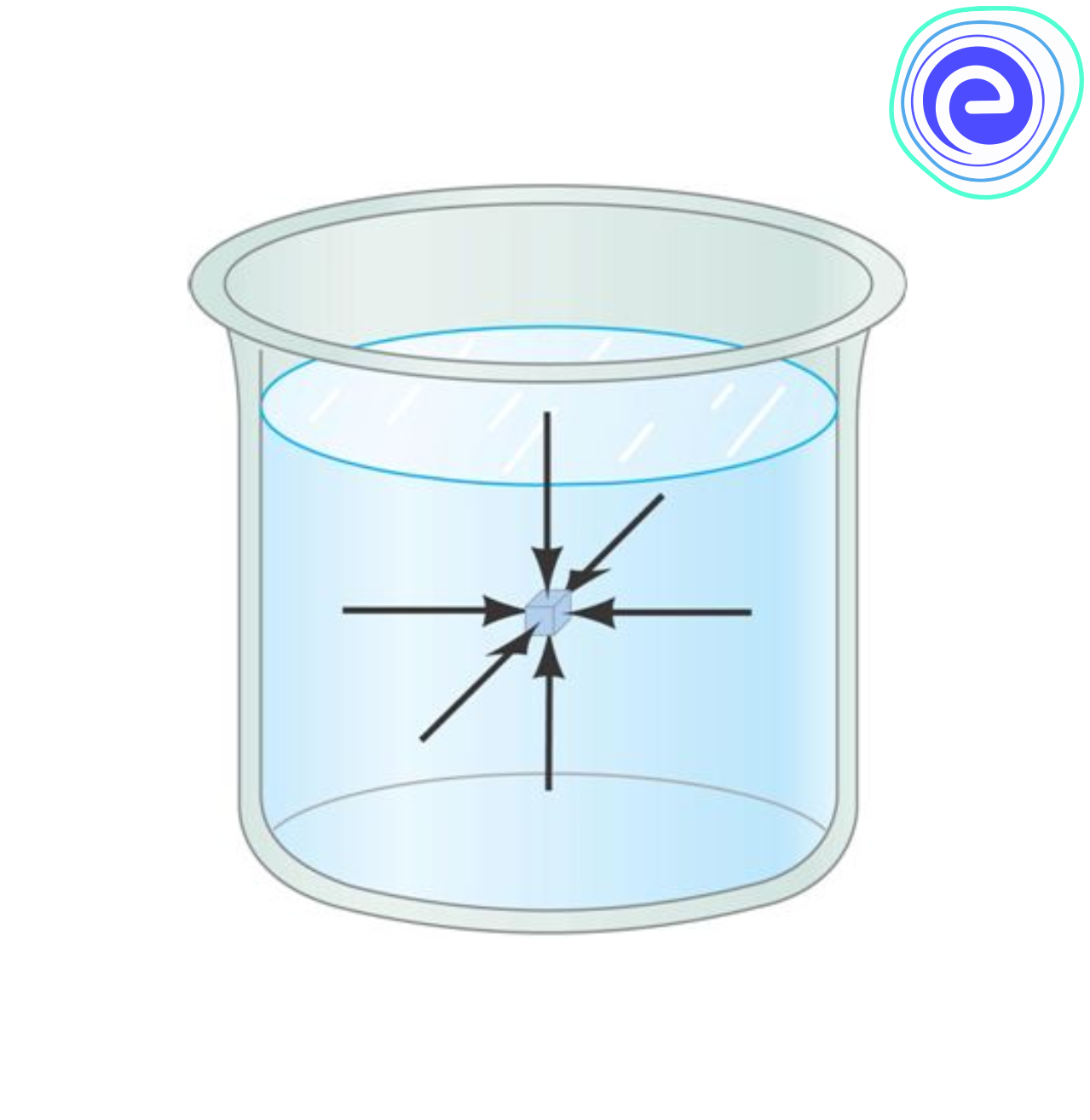
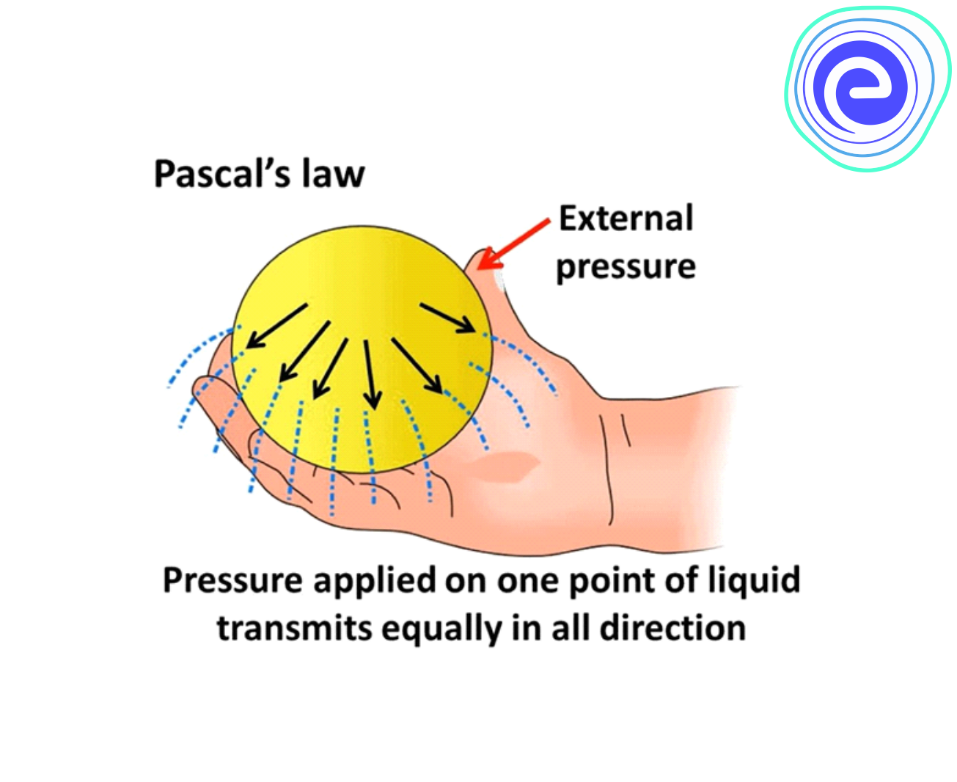
Pascal’s law was given by the French scientist Blaise pascal. According to this law, the pressure at all points at the same height within a fluid is the same, given that the fluid is at rest. In simple terms, Pascal’s law can be stated as – for a fluid contained in a vessel, the change in pressure in one part of the fluid is transmitted equally throughout the fluid and to the vessel’s walls. Pascal’s law is the principle behind the working of hydraulic machines like hydraulic presses or lifts.

Pressure Within the Fluid: Formula

The formula to calculate the pressure at a point within the fluid can be given as:

\({P_{fluid}} = P + \rho gh\)

Here, 

\({P_{fluid}}:\) Pressure at the required point within the fluid

\(P:\) Pressure at a reference point

\(g:\) Acceleration due to gravity, \({\rm{g}} = 9.8\;{\rm{m}}/{{\rm{s}}^2}\)

\(h:\) Height of the given point w.r.t. reference point:

\(\rho :\) Density of fluid

Pressure Within the Fluid: Derivation

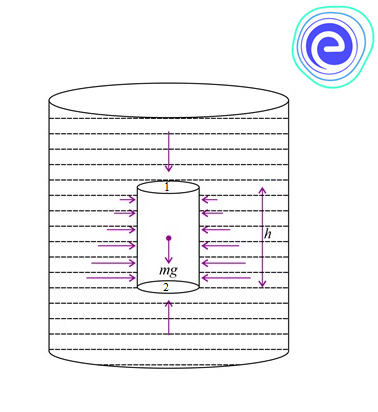
To derive the expression of pressure within a fluid, consider the diagram given below:

The fluid is at rest in a container. Take two points \(1\) and \(2\) within the fluid such that point \(1\) is directly at a height h above point \(2.\) Let the pressure at these two points be \({P_1}\) and \({P_2}\) respectively. Between the two points, consider a small cylindrical element of area \(A\) and height \(h.\) Since the fluid is at rest, thus no forces are acting on it in the horizontal direction. The weight of this cylindrical column will balance any forces in the vertical direction.

The forces in the vertical direction are the pressure at the top of the column, acting in the downward direction, and the pressure at the bottom, acting in the upward direction. Since force is equal to the product of pressure and area. Thus,

Force acting on the top, \({F_1} = {P_1} \times A\,{\rm{(downwards)}}\)

Force acting at the bottom, \({F_1} = {P_2} \times A\,{\rm{(upwards)}}\)

If \(m\) is the mass of the liquid column, then, 

Weight of the fluid cylinder, \(W = m \times g\)

Balancing the forces in the vertical direction, we get:

\({P_2}A – {P_1}A = mg\)

Or,

\(\left( {{P_2} – {P_1}} \right)A = mg \cdots (1)\)

Consider to be the density of the fluid, then,

\(\rho = \frac{m}{V} \ldots \left( 2 \right)\)

Where \(V\) is the volume of fluid within the column.

Since volume is equal to the product of area and height of the column. Thus, 

\(V = A \times h\)

Substitute this, in the above expression \((2),\) we get:

\(\rho = \frac{m}{{Ah}}\)

Or, \(m = \rho Ah\)

Put this value into equation \((1),\)

\(\left( {{P_2} – {P_1}} \right)A = \rho Ahg\)

\({P_2} – {P_1} = \rho hg \ldots .(3)\)

From the above result, we can conclude that the Pressure difference between two points within a liquid depends on:

1. The mass density of the fluid
2. The difference between the vertical heights of the points
3. Acceleration due to gravity

If point \(1\) lies at the top of the fluid, i.e., at the air-water interface. The pressure at point \(1\) will be equal to the atmospheric pressure. Replacing \({P_1}\) by the atmospheric pressure \(\left( {{P_a}} \right)\) and \({P_2}\) by \(P\) in equation \((3),\) we get:

\(P – {P_a} = \rho hg\)

Or, \(P = {P_a} + \rho hg\)

Thus, at depth below the surface of a liquid open to the atmosphere, the pressure \(P\) is greater than atmospheric pressure by a factor of \(\rho hg.\) Thus, as the depth of a point increases below the surface of the liquid, at rest, the pressure at that point increases. This means for liquid in a given container; pressure is minimum at the surface of the liquid.

This excess pressure at any point within the fluid at a depth \(h,\) i.e.,  \(P – {P_a}\) is called the gauge pressure.

The atmospheric pressure \({P_a}\) can be defined as the weight of the air column of a unit cross-sectional area extending the given point to the top of the atmosphere.

Mathematically, \({P_a} = \rho hg\)

Where \(\rho \) is the air density, \(h\) is the height of the air column at the reference point, and \(g\) is the acceleration due to gravity. 

At sea level, \({P_a} = 1.013 \times {10^5}\;{\rm{Pa}}.\)

Solved Examples on Pressure Inside a Fluid

Q.1. Calculate the pressure experienced by a scuba driver when she is \(10\) meters below the ocean’s surface. Take \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\)
Ans: Atmospheric pressure at the surface of the ocean, \({P_a} = 1.013 \times {10^5}\;{\rm{Pa}}\)
The pressure experienced by scuba driver, \(P = {P_a} + \rho hg\)
\(P = 1.013 \times {10^5} + (10)(10)\left( {1.03 \times {{10}^3}} \right) = 2.043 \times {10^5}\;{\rm{Pa}}\)

Q.2. How high would the atmosphere extend, given that the density of the atmosphere at sea level is \(1.29\;{\rm{kg}}/{{\rm{m}}^3}\) Take \({\rm{g}} = 10\;{\rm{m}}/{{\rm{s}}^2}\)
Ans: Atmospheric pressure at sea level, \({P_a} = 1.013 \times {10^5}\;{\rm{Pa}}\)
Atmospheric pressure, \({P_a} = \rho hg\)
\(1.013 \times {10^5}Pa = 1.29 \times 10 \times h\)
\(h = 7852\;{\rm{m}}\)

Summary

The pressure acting on a body is defined as the force per unit area that acts perpendicular to the body’s surface. It is a scalar quantity. Mathematically, \({P_{av}} = \frac{F}{A}\) and SI unit of pressure is Newton per metre square or \({\rm{N}}{{\rm{m}}^{ – 2}}.\)

Fluid, at rest, exerts a force on the surface of an object submerged in it. The force applied by a fluid always acts normal to the surface of the object. We use Pascal’s law to measure the pressure within a stationary fluid. Pascal’s law can be stated as – for a fluid contained in a vessel, the change in pressure in one part of the fluid is transmitted equally throughout the fluid and to the vessel’s walls.The formula to calculate the pressure at a point within the fluid can be given as: \({P_{fluid}} = P + \rho gh\)

Learn Everything About Pascal’s Law

Frequently Asked Questions On Pressure Inside a Fluid

Q.1. What is pressure?
Ans: Pressure is the perpendicular force acting per unit area of a surface.

Q.2. Give dimensions of density.
Ans: The dimensions of density are \(\left[ {{M^1}{L^{ – 3}}{T^0}} \right]\)

Q.3. What are the factors on which the pressure within depends?
Ans: It depends on:
Density of fluid
Depth of the point within the fluid
Acceleration due to gravity

Q.4. Define gauge pressure.
Ans: The excess pressure at a given depth within a fluid compared to the atmospheric pressure at the surface of the fluid is known as gauge pressure.

Q.5. State Pascal’s law.
Ans: Pascal’s law states that the pressure at all points at the same height within a fluid is the same, given that the fluid is at rest.

Now you are provided with all the necessary information on the pressure inside fluid and we hope this detailed article is helpful to you. If you have any queries regarding this article, please ping us through the comment section below and we will get back to you as soon as possible.