Product to Sum or Difference: The act of transforming sums into products, or products into sums, can be the difference between a simple answer and none at all. The sum and difference identities can create two sets of identities that aid in the conversion. The product sum identities are known as product‐sum identities.

We will establish the formula to transform the products of two sines or two cosines or one sine and one cosine into the sum or difference of two sines or two cosines. These formulas are derived from the formulas of sum and difference of angles of trigonometric functions. When solving the integrals of trigonometric functions, these formulas come in handy. The process of converting sums into products or products into sums can help us simplify many trigonometric equations and solve them.

Product to Sum or Difference Formulas

The product to sum or difference formulas are derived using the formulas of trigonometric functions of the sum and difference of two real numbers. There are four products to sum or difference formulas that are widely used as trigonometric identities.

\(\sin A\cos B = \frac{1}{2}\left[ {\sin \left( {A + B} \right) + \sin \left( {A – B} \right)} \right]\)
\(\cos A\sin B = \frac{1}{2}\left[ {\sin \left( {A + B} \right) – \sin \left( {A – B} \right)} \right]\)
\(\cos A\cos B = \frac{1}{2}\left[ {\cos \left( {A + B} \right) + \cos \left( {A – B} \right)} \right]\)
\(\sin A\sin B = \frac{1}{2}\left[ {\cos \left( {A – B} \right) – \cos \left( {A + B} \right)} \right]\)

Know the Trigonometric Identities

Trigonometric Functions of Sum and Difference of Two Real Numbers

There are four formulas for sine and cosine functions of sum and difference of two real numbers.

\(\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B\)
\(\sin \left( {A – B} \right) = \sin A\cos B – \cos A\sin B\)
\(\cos \left( {A + B} \right) = \cos A\cos B – \sin A\sin B\)
\(\cos \left( {A – B} \right) = \cos A\cos B + \sin A\sin B\)

Derivation of Trigonometric Ratios of Sum and Difference of Two Real Numbers

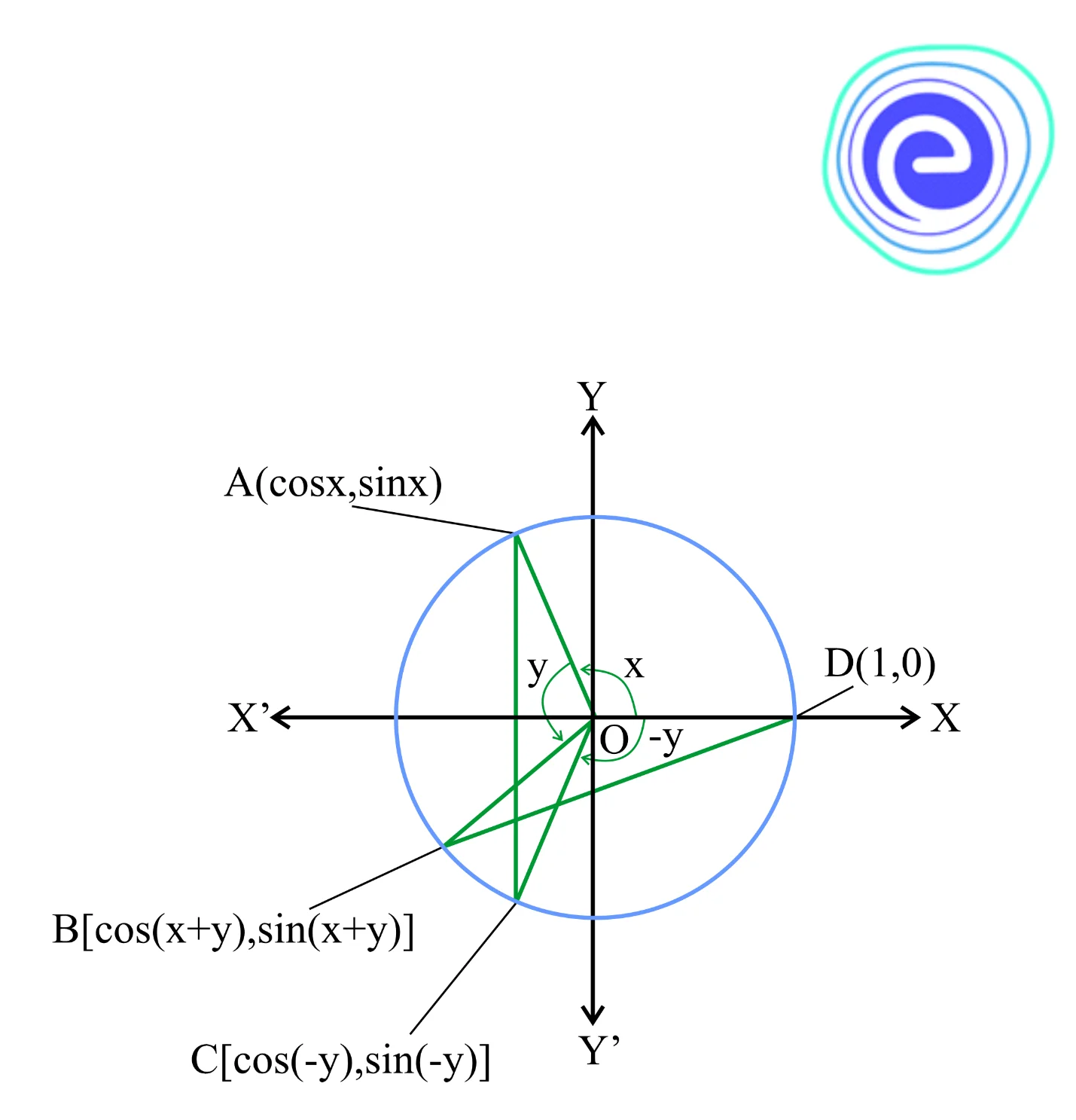
Consider a unit circle with centre at the origin, \(o\)
Let
\(\angle DOA = x\)
\(\angle AOB = y\)
Then,
\(\angle DOB = x + y\)
\(\angle DOC = – y\)
Therefore, the coordinates of \(A,B,C\) and \(D\) are as follows:
\(A = \left( {\cos x,\sin x} \right)\)
\(B = \left[ {\cos \left( {x + y} \right),\sin \left( {x + y} \right)} \right]\)
\(C = \left[ {\cos \left( { – y} \right),\sin \left( { – y} \right)} \right]\)
\(D = \left( {1,0} \right)\)
Now, consider \(\Delta AOC,\) and \(\Delta BOD,\)
\(AO = OB…..\left( i \right)\) [Radii of the circle]
Since \(\angle AOB = \angle COD,\) adding \(\angle BOC\) to both sides, we have,
\(\angle AOC = \angle BOD…..\left( {ii} \right)\)
Also, \(OC = OD…..\left( {iii} \right)\)
[Radii of the circle]
From \(\left( i \right),\,\left( {ii} \right)\) and \(\left( {iii} \right)\)
by \(SAS\) congruency rule, we have,
\(AC = BD\)
\( \Rightarrow A{C^2} = B{D^2}\)
\( \Rightarrow {\left[ {\cos x – \cos \left( { – y} \right)} \right]^2} + {\left[ {\sin x – \sin \left( { – y} \right)} \right]^2} = {\left[ {1 – \cos \left( {x + y} \right)} \right]^2} + {\left[ {0 – \sin \left( {x + y} \right)} \right]^2}\)
\( \Rightarrow 2 – 2\left( {\cos x\cos y – \sin x\sin y} \right) = 2 – 2\cos \left( {x + y} \right)\)
\( \Rightarrow \cos \left( {x + y} \right) = \left( {\cos x\cos y – \sin x\sin y} \right)\)
Hence, \(\cos \left( {x + y} \right) = \left( {\cos x\cos y – \sin x\sin y} \right) \ldots \left( {iv} \right)\)
Putting \(y = – y\) in equation \(\left( {iv} \right),\)
\(\cos \left( {x + \left( { – y} \right)} \right) = \left( {\cos x\cos \left( { – y} \right) – \sin x\sin \left( { – y} \right)} \right)\)
\(\cos \left( {x – y} \right) = \cos x\cos y + \sin x\sin y\) [Since \(\cos \left( { – y} \right) = \cos y,\) and \(\sin \left( { – y} \right) = – \sin y\)]
Now,
\(\sin \left( {x + y} \right) = \cos \left( {\frac{\pi }{2} – \left( {x + y} \right)} \right) = \cos \left( {\left( {\frac{\pi }{2} – x} \right) – y} \right)\)
Now,
\(\cos \left( {\left( {\frac{\pi }{2} – x} \right) – y} \right) = \cos \left( {\frac{\pi }{2} – x} \right)\cos y + \sin \left( {\frac{\pi }{2} – x} \right)\sin y\)
\( = \sin x\cos y + \cos x\sin y\)
Thus, \(\sin (x – y) = \sin x\cos y + \cos x\sin y \ldots \ldots (v)\)
Replacing \(y\) by \( – y\) in equation \(\left( v \right),\) we have
\(\sin \left( {x + y} \right) = \sin x\cos \left( { – y} \right) – \cos x\sin \left( { – y} \right)\)
Since \(\cos \left( { – y} \right) =\cos y,\sin \left( { – y} \right) = – \sin y\)
\(\Rightarrow \sin \left( {x + y} \right) = \sin x\cos y + \cos x\sin y\)

Derivation of Product to Sum or Difference Formulas

1. \(2\sin A\cos B = \sin \left( {A + B} \right) + \sin \left( {A – B} \right):\)
   From the formulas of sum or difference of two real numbers of sine functions, we have,
   \(\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B…..\left( i \right)\)
   \(\sin \left( {A – B} \right) = \sin A\cos B – \cos A\sin B…..\left( {ii} \right)\)
   Adding equations \(\left( i \right),\) and \(\left( ii \right),\) we have,
   \(2\sin A\cos B = \sin \left( {A + B} \right) + \sin \left( {A – B} \right)\)
2. \(2\cos A\sin B = \sin \left( {A + B} \right) – \sin \left( {A – B} \right):\)
   Subtracting equation \(\left( {ii} \right)\) from equation \(\left( i \right),\) we have
   \(2\cos A\sin B = \sin \left( {A + B} \right) – \sin \left( {A – B} \right)\)
3. \(2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A – B} \right):\)
   From the formulas of sum or difference of two real numbers of cosine functions, we have
   \(\cos \left( {A + B} \right) = \cos A\cos B – \sin A\sin B….\left( {iii} \right)\)
   \(\cos \left( {A – B} \right) = \cos A\cos B + \sin A\sin B….\left( {iv} \right)\)
   Adding equations \(\left( {iii} \right),\) and \(\left( {iv} \right),\) we have
   \(2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A – B} \right)\)
4. \(2\sin A\sin B = \cos \left( {A – B} \right) – \cos \left( {A + B} \right):\)
   Subtracting equation \(\left( {iii} \right)\) from equation \(\left( {iv} \right),\) we have
   \(2\sin A\sin B = \cos \left( {A – B} \right) – \cos \left( {A + B} \right)\)

Sum or Difference to Product Formulas

Just like the product to sum formulas, the sum-to-product formulas allow us to express sums of sine or cosine as products. These formulas are derived from the product to sum or difference formulas of trigonometric functions.

The formulas are given as follows:

\(\sin A + \sin B = 2\sin \left( {\frac{{A + B}}{2}} \right)\cos \left( {\frac{{A – B}}{2}} \right)\)
\(\sin A – \sin B = 2\cos \left( {\frac{{A + B}}{2}} \right)\sin \left( {\frac{{A – B}}{2}} \right)\)
\(\cos A + \cos B = 2\cos \left( {\frac{{A + B}}{2}} \right)\cos \left( {\frac{{A – B}}{2}} \right)\)
\(\cos A – \cos B = – 2\sin \left( {\frac{{A + B}}{2}} \right)\sin \left( {\frac{{A – B}}{2}} \right)\)
The derivation of these formulas is explained in the next article.

Solved Examples – Product to Sum or Difference Formulas

Q.1. Convert \(2\sin 5x\cos x\) into the sum or difference of sine and cosine functions.
Ans: Given, \(2\sin 5x\cos x\)
Using \(2\sin A\cos B = \sin \left( {A + B} \right) + \sin \left( {A – B} \right)\)
Here \(A = 5x,\) and \(B = x\)
\(\therefore 2\sin 5x\cos x = \sin \left( {5x + x} \right) + \sin \left( {5x – x} \right)\)
\( = \sin \left( {6x} \right) + \sin \left( {4x} \right)\)
Hence, \(2\sin 5x\cos x = \sin \left( {6x} \right) + \sin \left( {4x} \right)\)

Q.2. Find the value of \(\cos {20^ \circ }\cos {40^ \circ }\cos {60^ \circ }\cos {80^ \circ }.\)
Ans: Given: \(\cos {60^ \circ }(\cos {20^ \circ }\cos {40^ \circ })\cos {80^ \circ }\)
\( = \frac{1}{2} \times \frac{1}{2}\left( {2\cos {{20}^ \circ }\cos {{40}^ \circ }} \right)\cos {80^ \circ }\)
Since \(2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A – B} \right),\) we have,
\( = \frac{1}{4}\left[ {\left\{ {\cos \left( {{{40}^ \circ } + {{20}^ \circ }} \right) + \cos \left( {{{40}^ \circ } – {{20}^ \circ }} \right)} \right\}\cos {{80}^ \circ }} \right]\)
\( = \frac{1}{4}\left\{ {\left( {\cos {{60}^ \circ } + \cos {{20}^ \circ }} \right)\cos {{80}^ \circ }} \right\}\)
\( = \frac{1}{4}\left\{ {\left( {\frac{1}{2} + \cos {{20}^ \circ }} \right)\cos {{80}^ \circ }} \right\}\)
\( = \frac{1}{4}\left\{ {\frac{1}{2}\cos {{80}^ \circ } + \cos {{80}^ \circ }\cos {{20}^ \circ }} \right\}\)
\( = \frac{1}{8}\left\{ {\cos {{80}^ \circ } + 2\cos {{80}^ \circ }\cos {{20}^ \circ }} \right\}\)
\({\kern 1pt} = \frac{1}{8}\left[ {\cos {{80}^ \circ } + \left\{ {\cos \left( {{{80}^ \circ } + {{20}^ \circ }} \right) + \cos \left( {{{80}^ \circ } – {{20}^ \circ }} \right)} \right\}} \right]\)
\(\left[ {\because 2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A – B} \right)} \right]\)
\( = \frac{1}{8}\left\{ {\cos {{80}^ \circ } + \cos {{100}^ \circ } + \cos {{60}^ \circ }} \right\}\)
\( = \frac{1}{8}\left\{ {\cos {{80}^ \circ } + \cos \left( {{{180}^ \circ } – {{80}^ \circ }} \right) + \cos {{60}^ \circ }} \right\}\)
\( = \frac{1}{8}\left\{ {\cos {{80}^ \circ } – \cos {{80}^ \circ } + \cos {{60}^ \circ }} \right\}\)
\( = \frac{1}{8}\left\{ {\cos {{80}^ \circ } – \cos {{80}^ \circ } + \frac{1}{2}} \right\}\)
\( = \frac{1}{8} \times \frac{1}{2}\)
\( = \frac{1}{{16}}\)
Hence, \(\cos {20^ \circ }\cos {40^ \circ }\cos {60^ \circ }\cos {80^ \circ } = \frac{1}{{16}}\)

Q.3. Prove that \(\sin A\sin \left( {\frac{\pi }{3} – A} \right)\sin \left( {\frac{\pi }{3} + A} \right) = \frac{1}{4}\sin 3A\)
Ans: \({\text{LHS}} = \sin A\sin \left( {\frac{\pi }{3} – A} \right)\sin \left( {\frac{\pi }{3} + A} \right)\)
\( = \frac{1}{2}\sin A\left\{ {2\sin \left( {\frac{\pi }{3} – A} \right)\sin \left( {\frac{\pi }{3} + A} \right)} \right\}\)
\( = \frac{1}{2}\sin A\left[ {\cos \left\{ {\left( {\frac{\pi }{3} – A} \right) – \left( {\frac{\pi }{3} + A} \right)} \right\} – \cos \left\{ {\left( {\frac{\pi }{3} – A} \right) + \left( {\frac{\pi }{3} + A} \right)} \right\}} \right]\)
\( = \frac{1}{2}\sin A\left\{ {\cos \left( { – 2A} \right) – \cos \frac{{2\pi }}{3}} \right\}\)
\( = \frac{1}{2}\sin A\left\{ {\cos \left( { – 2A} \right) – \cos \left( {\pi – \frac{\pi }{3}} \right)} \right\}\)
\( = \frac{1}{2}\sin A\left\{ {\cos \left( { – 2A} \right) + \cos \left( {\frac{\pi }{3}} \right)} \right\}\)
\( = \frac{1}{2}\sin A\left\{ {\cos 2A + \frac{1}{2}} \right\}\)
\( = \frac{1}{2}\sin A\cos 2A + \frac{1}{4}\sin A\)
\( = \frac{1}{4}\left\{ {\sin \left( {A + 2A} \right) + \sin \left( {A – 2A} \right)} \right\} + \frac{1}{4}\sin A\)
\( = \frac{1}{4}\left\{ {\sin 3A + \sin \left( { – A} \right) + \frac{1}{4}\sin A} \right\}\)
\( = \frac{1}{4}\sin 3A\quad \left[ {\because \sin \left( { – A} \right) = – \sin A} \right]\)
\( = {\text{R}}{\text{.H}}{\text{.S}}\)
Hence, proved

Q.4. If \(\cos \left( {A + B} \right)\sin \left( {C – D} \right) = \cos \left( {A – B} \right)\sin \left( {C + D} \right)\) then find the value of \(\tan A\tan B\tan C + \tan D.\)
Ans: Consider \(\cos \left( {A + B} \right)\sin \left( {C – D} \right) = \cos \left( {A – B} \right)\sin \left( {C + D} \right)\)
\( \Rightarrow \frac{{\cos \left( {A + B} \right)}}{{\cos \left( {A – B} \right)}} = \frac{{\sin \left( {C + D} \right)}}{{\sin \left( {C – D} \right)}}\)
Applying componendo and dividendo, we get
\(\frac{{\cos \left( {A + B} \right) + \cos \left( {A – B} \right)}}{{\cos \left( {A + B} \right) – \cos \left( {A – B} \right)}} = \frac{{\sin \left( {C + D} \right) + \sin \left( {C – D} \right)}}{{\sin \left( {C + D} \right) – \sin \left( {C – D} \right)}}\)
\( \Rightarrow \frac{{2\cos A\cos B}}{{ – 2\sin A\sin B}} = \frac{{2\sin C\cos D}}{{2\cos C\sin D}}\)
\( \Rightarrow – \cot A\cot B = \tan C\cot D\)
\( \Rightarrow – \frac{1}{{\tan A}} \times \frac{1}{{\tan B}} = \tan C \times \frac{1}{{\tan D}}\)
\( \Rightarrow \tan A\tan B\tan C = – \tan D\)
Hence, \(\tan A\tan B\tan C + \tan D = 0\)

Q.5. Find the value of \(2\cos \frac{\pi }{{13}}\cos \frac{{9\pi }}{{13}} + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}}.\)
Ans: Consider \(2\cos \frac{\pi }{{13}}\cos \frac{{9\pi }}{{13}} + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}}\)
\( = \cos \left( {\frac{{9\pi }}{{13}} + \frac{\pi }{{13}}} \right) + \cos \left( {\frac{{9\pi }}{{13}} – \frac{\pi }{{13}}} \right) + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}}\) \(\left[ {\because 2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A – B} \right)} \right]\)
\( = \cos \frac{{10\pi }}{{13}} + \cos \frac{{8\pi }}{{13}} + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}}\)
\( = \cos \left( {\pi – \frac{{3\pi }}{{13}}} \right) + \cos \left( {\pi – \frac{{5\pi }}{{13}}} \right) + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}}\)
\( = – \cos \frac{{3\pi }}{{13}} – \cos \frac{{5\pi }}{{13}} + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}}\)
\( = 0\)
Hence,
\(2\cos \frac{\pi }{{13}}\cos \frac{{9\pi }}{{13}} + \cos \frac{{3\pi }}{{13}} + \cos \frac{{5\pi }}{{13}} = 0\)

Q.6. If \(\alpha + \beta = {90^ \circ },\) find the maximum and minimum values of \(\sin \alpha \sin \beta .\)
Ans: Given, \(\alpha + \beta = {90^ \circ },\)
Let \(y = \sin \alpha \sin \beta .\) Then,
\(y = \frac{1}{2}\left( {2\sin \alpha \sin \beta } \right)\)
\( = \frac{1}{2}\left\{ {\cos \left( {\alpha – \beta } \right) – \cos \left( {\alpha + \beta } \right)} \right\}\)
\( = \frac{1}{2}\left\{ {\cos \left( {\alpha – \beta } \right) – \cos {{90}^ \circ }} \right\}\)
\( = \frac{1}{2}\cos \left( {\alpha – \beta } \right)\)
We know that \( – 1 \leqslant \cos (\alpha – \beta ) \leqslant 1\)
\( \Rightarrow \frac{{ – 1}}{2} \leqslant \frac{1}{2}\cos \left( {\alpha – \beta } \right) \leqslant \frac{1}{2}\)
\( \Rightarrow \frac{{ – 1}}{2} \leqslant y \leqslant \frac{1}{2}\)
\( \Rightarrow \frac{{ – 1}}{2} \leqslant \sin \alpha \sin \beta \leqslant \frac{1}{2}\)
Hence, \( – \frac{1}{2}\) and \(\frac{1}{2}\) are respectively the minimum and maximum values of \(\sin \alpha \sin \beta .\)

Q.7. Show that \(\tan \left( {{{60}^ \circ } + A} \right)\tan \left( {{{60}^ \circ } – A} \right) = \frac{{2\cos 2A + 1}}{{2\cos 2A – 1}}\)
Ans: To prove \(\tan \left( {{{60}^ \circ } + A} \right)\tan \left( {{{60}^ \circ } – A} \right) = \frac{{2\cos 2A + 1}}{{2\cos 2A – 1}}\)
\({\rm{ L}}{\rm{.H}}{\rm{.S }} = \tan \left( {{{60}^ \circ } + {\rm{A}}} \right)\tan \left( {{{60}^ \circ } – {\rm{A}}} \right)\)
\( = \frac{{\sin \left( {{{60}^ \circ } + {\rm{A}}} \right)\sin \left( {{{60}^ \circ } – {\rm{A}}} \right)}}{{\cos \left( {{{60}^ \circ } + {\rm{A}}} \right)\cos \left( {{{60}^ \circ } – {\rm{A}}} \right)}}\)
\( = \frac{{2\sin \left( {{{60}^ \circ } + {\rm{A}}} \right)\sin \left( {{{60}^ \circ } – {\rm{A}}} \right)}}{{2\cos \left( {{{60}^ \circ } + {\rm{A}}} \right)\cos \left( {{{60}^ \circ } – {\rm{A}}} \right)}}\)
\( = \frac{{\cos \left\{ {\left( {{{60}^ \circ } + {\text{A}}} \right) – \left( {{{60}^ \circ } – {\text{A}}} \right)} \right\} – \cos \left\{ {\left( {{{60}^ \circ } + {\text{A}}} \right) + \left( {{{60}^ \circ } – {\text{A}}} \right)} \right\}}}{{\cos \left\{ {\left( {{{60}^ \circ } + {\text{A}}} \right) + \left( {{{60}^ \circ } – {\text{A}}} \right)} \right\} + \cos \left\{ {\left( {{{60}^ \circ } + {\text{A}}} \right) – \cos \left( {{{60}^ \circ } – {\text{A}}} \right)} \right\}}}\) \((\because 2\sin A\sin B = \cos (A – B) – \cos (A + B),2\cos A\cos B = \cos (A + B) + \cos (A – B))\)
\( = \frac{{\cos 2A – \cos {{120}^ \circ }}}{{\cos {{120}^ \circ } + \cos 2A}}\)
\( = \frac{{\cos 2A – \left( { – \frac{1}{2}} \right)}}{{ – \frac{1}{2} + \cos 2A}}\)
\( = \frac{{2\cos 2A + 1}}{{2\cos 2A – 1}} = {\rm{R}}{\rm{.H}}{\rm{.S}}{\rm{.}}\)
Hence, Proved.

Q.8. Prove that \(\frac{{\sin 8\theta \cos \theta – \cos 3\theta \sin 6\theta }}{{\cos 2\theta \cos \theta – \sin 3\theta \sin 4\theta }} = \tan 2\theta .\)
Ans: To prove \(\frac{{\sin 8\theta \cos \theta – \cos 3\theta \sin 6\theta }}{{\cos 2\theta \cos \theta – \sin 3\theta \sin 4\theta }} = \tan 2\theta .\)
\({\text{L}}{\text{.H}}{\text{.S}}. = \frac{{\sin 8\theta \cos \theta – \cos 3\theta \sin 6\theta }}{{\cos 2\theta \cos \theta – \sin 3\theta \sin 4\theta }}\)
\( = \frac{{2\sin 8\theta \cos \theta – 2\cos 3\theta \sin 6\theta }}{{2\cos 2\theta \cos \theta – 2\sin 3\theta \sin 4\theta }}\)
\( = \frac{{\left[ {\sin \left( {8\theta + \theta } \right) + \sin \left( {8\theta – \theta } \right)} \right] – \left[ {\sin \left( {3\theta + 6\theta } \right) – \sin \left( {3\theta – 6\theta } \right)} \right]}}{{\left[ {\cos \left( {2\theta + \theta } \right) + \cos \left( {2\theta – \theta } \right)} \right] – \left[ {\cos \left( {3\theta – 4\theta } \right) – \cos \left( {3\theta + 4\theta } \right)} \right]}}\)
\( = \frac{{\left[ {\sin \,9\theta + \sin \,7\theta } \right] – \left[ {\sin \,9\theta + \sin \,3\theta } \right]}}{{\left[ {\cos \,3\theta + \cos \,\theta } \right] – \left[ {\cos \left( { – \theta } \right) – \cos \,7\theta } \right]}}\)
\( = \frac{{\sin 7\theta – \sin 3\theta }}{{\cos 3\theta + \cos 7\theta }}\)
\( = \frac{{2 \cdot \cos \left( {\frac{{7\theta + 3\theta }}{2}} \right)\sin \left( {\frac{{7\theta – 3\theta }}{2}} \right)}}{{2 \cdot \cos \left( {\frac{{3\theta + 7\theta }}{2}} \right)\cos \left( {\frac{{3\theta – 7\theta }}{2}} \right)}}\)
\( = \frac{{2 \cdot \cos 5\theta \sin 2\theta }}{{2 \cdot \cos 5\theta \cos \left( { – 2\theta } \right)}}\)
\( = \frac{{2 \cdot \cos 5\theta \sin 2\theta }}{{2 \cdot \cos 5\theta \cos 2\theta }}\)
\( = \tan 2\theta \)
\({\text{ = R}}{\text{.H}}{\text{.S}}\)
Hence Proved.

Q.9. Prove that \(\cos A\cos \left( {\frac{\pi }{3} – A} \right)\cos \left( {\frac{\pi }{3} + A} \right) = \frac{1}{4}\cos 3A\)
Ans: \({\text{L}}{\text{.H}}{\text{.S}} = \cos A\cos \left( {\frac{\pi }{3} – A} \right)\cos \left( {\frac{\pi }{3} + A} \right)\)
\( = \frac{1}{2}\cos A\left\{ {2\cos \left( {\frac{\pi }{3} – A} \right)\cos \left( {\frac{\pi }{3} + A} \right)} \right\}\)
\( = \frac{1}{2}\cos A\left[ {\cos \left\{ {\left( {\frac{\pi }{3} – A} \right) + \left( {\frac{\pi }{3} + A} \right)} \right\} + \cos \left\{ {\left( {\frac{\pi }{3} – A} \right) – \left( {\frac{\pi }{3} + A} \right)} \right\}} \right]\)
\( = \frac{1}{2}\cos A\left\{ {\cos \frac{{2\pi }}{3} + \cos \left( { – 2A} \right)} \right\}\)
\( = \frac{1}{2}\cos A\left\{ {\cos \frac{{2\pi }}{3} + \cos 2A} \right\}\)
\( = \frac{1}{2}\cos A\left\{ { – \frac{1}{2} + \cos 2A} \right\}\)
\( = – \frac{1}{4}\cos A + \frac{1}{2}\cos A\cos 2A\)
\( = – \frac{1}{4}\cos A + \frac{1}{4}\left( {2\cos 2A\cos A} \right)\)
\( = – \frac{1}{4}\cos A + \frac{1}{4}\left\{ {\cos \left( {2A + A} \right) + \cos \left( {2A – A} \right)} \right\}\)
\( = – \frac{1}{4}\cos A + \frac{1}{4}\left( {\cos 3A + \cos A} \right)\)
\( = \frac{1}{4}\cos 3A\)
\( = {\text{R}}{\text{.H}}{\text{.S}}\)
Hence proved.

Q.10. Find the value of the following function by expressing the given product into the sum or difference of sines and cosines:\(\cos \frac{{5\pi }}{{12}}\cos \frac{\pi }{{12}}\)
Ans: Given: \(\cos \frac{{5\pi }}{{12}}\cos \frac{\pi }{{12}}\)
\( = \frac{1}{2}\left( {2\cos \frac{{5\pi }}{{12}}\cos \frac{\pi }{{12}}} \right)\)
\( = \frac{1}{2}\left\{ {\cos \left( {\frac{{5\pi }}{{12}} + \frac{\pi }{{12}}} \right) + \cos \left( {\frac{{5\pi }}{{12}} – \frac{\pi }{{12}}} \right)} \right\}\)
\( = \frac{1}{2}\left\{ {\cos \frac{{6\pi }}{{12}} + \cos \frac{{4\pi }}{{12}}} \right\}\)
\( = \frac{1}{2}\left\{ {\cos \frac{\pi }{2} + \cos \frac{\pi }{3}} \right\}\)
\(\frac{1}{2}\left\{ {0 + \frac{1}{2}} \right\}\)
\( = \frac{1}{4}\)
Hence, the required value is \( = \frac{1}{4}.\)

Summary

The trigonometric identities are the product-to-sum formulas that can help us rewrite products of sines, products of cosines, and products of sine and cosine as sums or differences of the individual ratios. These identities are derived by adding or subtracting the sum and difference formulas for sine and cosine. It is a good idea to memorise these identities if we can since they will help us reduce more complicated trigonometric problems and help us prove other trigonometric statements.

Frequently Asked Questions (FAQs)

Q.1. How do you prove products to sum identities?
Ans: The product-to-sum formulae may be found by noting that the sum and difference formulas for sine and cosine seem quite similar, except with opposite signs in the centre. We may then cancel terms by combining the formulae.

Q.2. What is the formula of \(\sin C – \sin D\)?
Ans: \(\sin C – \sin D = 2\cos \left( {\frac{{C + D}}{2}} \right)\sin \left( {\frac{{C – D}}{2}} \right)\)

Q.3. How do you write a product as a sum or difference of trigonometric functions?
Ans: The formulas for the product to sum or difference of trigonometric functions are given as follows:
\(2\sin A\cos B = \sin \left( {A + B} \right) + \sin \left( {A – B} \right)\)
\(2\cos A\sin B = \sin \left( {A + B} \right) – \sin \left( {A – B} \right)\)
\(2\cos A\cos B = \cos \left( {A + B} \right) + \cos \left( {A – B} \right)\)
\(2\sin A\sin B = \cos \left( {A – B} \right) – \cos \left( {A + B} \right)\)

Q.4. What is the purpose of product-to-sum identities?
Ans: To convert the product between sines and/or cosines into a sum or difference, the product-to-sum identities are utilised. These identities are obtained by adding or subtracting the sine and cosine sum and difference formulas.

Q.5. How do you find the sum of trigonometric ratios?
Ans: The sum of trigonometric ratios are found using the following identities.
\(\sin A + \sin B = 2\sin \left( {\frac{{A + B}}{2}} \right)\cos \left( {\frac{{A – B}}{2}} \right)\)
\(\cos A + \cos B = 2\cos \left( {\frac{{A + B}}{2}} \right)\cos \left( {\frac{{A – B}}{2}} \right)\)

Q.6. What is sum of product?
Ans: The sum of product of trigonometric functions can be expressed as sum or difference of their angles as follows:
\(\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B\)
\(\sin \left( {A – B} \right) = \sin A\cos B – \cos A\sin B\)
\(\cos \left( {A + B} \right) = \cos A\cos B – \sin A\sin B\)
\(\cos \left( {A – B} \right) = \cos A\cos B + \sin A\sin B\)

Q.7. How do you remember the sum and difference identities?
Ans: The sum and difference identities of trigonometric functions are given as follows:
\(\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B\)
\(\sin \left( {A – B} \right) = \sin A\cos B – \cos A\sin B\)
\(\cos \left( {A + B} \right) = \cos A\cos B – \sin A\sin B\)
\(\cos \left( {A – B} \right) = \cos A\cos B + \sin A\sin B\)
Observe that corresponding to sine function in the L.H.S., we have product of both sine and cosine functions then their sum or difference in R.H.S. When we have cosine function in L.H.S., then in R.H.S. we have product of either sine function or cosine function.
And, now we observe the signs:
For sine functions, the sign is the same on both the sides, whereas, for cosine functions, the signs are different.

Q.8. How do you use angle sum or difference identity?
Ans: Angle sum or difference identities can be used to find the function values of any angle which can be expressed as a sum or difference using the familiar values for the sine, cosine and tangent of the \({30^ \circ },{45^ \circ },{60^ \circ }\) and \({90^ \circ }\) angles and their multiples.
For Example: The value of \(\sin {75^ \circ }\) is found as follows:
\(\sin {75^ \circ } = \sin \left( {{{45}^ \circ } + {{30}^ \circ }} \right) = \sin {45^ \circ }\cos {30^ \circ } + \cos {45^ \circ }\sin {30^ \circ }\)
\( = \frac{1}{{\sqrt 2 }} \times \frac{{\sqrt 3 }}{2} + \frac{1}{{\sqrt 2 }} \times \frac{1}{2}\)
\(\therefore \sin {75^ \circ } = \frac{{\sqrt 3 + 1}}{{2\sqrt 2 }}\)

Learn all About Trigonometric Ratios

We hope this detailed article on the Product of Trigonometric Ratio to Sum, Difference was helpful. If you have any doubts, let us know about them in the comment section below. Our team will get try to solve your queries at the earliest.