Properties of Whole Numbers: Definitions, Types, and Examples

Properties of Whole Numbers: We begin to count the numbers as \(1,2,3,4, \ldots \). They come naturally when we start counting. Hence, mathematicians call them counting numbers. If we add \(1\) to any natural number, we will get a number called the successor, and if we subtract \(1\) to any natural number, we will get a number called the predecessor.

Does \(1\) have both successor and predecessor? No, the number \(1\) has no predecessor in natural numbers. To the set of natural numbers, if we add zero as the predecessor for \(1\), then it forms the group of whole numbers. That is, \(0,1,2,3, \ldots \) are called whole numbers. Let us learn the different properties of whole numbers.

What are Whole Numbers?

We have learnt that numbers \(1,2,3,4, \ldots \) etc., are called natural numbers. These natural numbers, along with the number zero, form the collection of whole numbers. That is, numbers \(0,1,2,3, \ldots \) are called whole numbers.

Following are some properties of whole numbers:

(i)  The number \(0\) is the first and the smallest whole number.
(ii) There is no last or largest whole number.
(iii) There are infinitely many or uncountable numbers of whole numbers.
(iv) All natural numbers are whole numbers.
(v) All whole numbers are not natural numbers. For example, \(0\) is a whole number, but it is not a natural number.

Learn All the Concepts on Whole Numbers

Representation of Whole Numbers on Number Line

The relationship between whole numbers and their properties can be understood by picturising them. For this, we represent whole numbers on a line called a number line. Representation of whole numbers on the number line also helps us compare two whole numbers, i.e., to decide which of the two given whole numbers is greater or smaller.

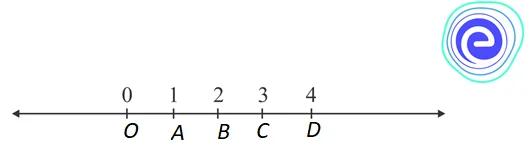
To represent whole numbers on a number line, we draw a straight line and mark a point \(O\). Starting from \(O\), mark points \(A, B, C, D,\) etc., on the line at equal distances to \(O’s\) right.

Label the point \(O\) as \(0\). Let us take \(O A = 1\) unit. So, \(A B = B C = C D = 1\) unit
Now, \(O B = O A + A B = 1 + 1 = 2\) units.
\(O C = O B + B C = 2 + 1 = 3\) units
\(O D = O C + C D = 3 + 1 = 4\) units

Since \(O\) corresponds to the whole number \(0, A, B, C, D,\) etc., correspond to the whole numbers \(1,2,3,4\) etc. So, on the number line against \(A, B, C, D,\) etc., we write \(1,2,3,4\) etc., respectively, as shown in the above figure.

Continuing in this manner, we can represent every whole number by some point on the number line. The arrow marks on both ends of the line indicate that the number line extends indefinitely on both sides.

Properties of Whole Numbers

We are familiar with four fundamental operations of addition, subtraction, multiplication and division. In this article, we will learn about the properties of these operations on whole numbers. Understanding these properties will help us find the short-cuts for calculations involving addition, subtraction and multiplication. Moreover, these proportions help us to understand the numbers better. The properties are listed below.

1. Closure Property
2. Commutative Property
3. Associative Property
4. Distributive Property

Closure Property of Addition of Whole Numbers

If \(a\) and \(b\) are two whole numbers, then \(a + b\) is also a whole number. In other words, the sum of any two whole numbers is a whole number.

Example: \(7 + 8 = 15\). Here, \(7\) and \(8\) are whole numbers, and their sum \(15\) is also a whole number.

Commutative Property of Addition of Whole Numbers

If \(a\) and \(b\) are any two whole numbers, then \(a + b = b + a\). In other words, the sum of two whole numbers remains the same even if the order of whole numbers is changed.

Example: \(9 + 8 = 8 + 9 = 17\)

Additive Identity of a Whole Number

If \(a\) is a whole number, then \(a + 0 = a = 0 + a\). In other words, the sum of any whole number and zero is the number itself. Zero is the only whole number that does not change the value of the number it is added to.

The whole number \(0\) is called the identity of the whole number.

Example: \(8 + 0 = 8 = 0 + 8\)

Associative Property of Addition of Whole Numbers

If \(a, b, c\) are any three whole numbers, then \(\left({a + b} \right) + c = a + \left({b + c} \right)\). In other words, the addition of whole numbers is associative.

Example: \(2 + (5 + 8) = (2 + 5) + 8 = 15\)

Subtraction Properties of Whole Numbers

Below are the properties of subtraction of whole numbers.
1. If \(a\) and \(b\) are two whole numbers such that \(a > b\) or \(a = b\), then \(a – b\) is a whole number. If \(a < b\), then subtraction \(a – b\) is not possible in whole numbers.
2. The subtraction of whole numbers is not commutative; that is, if \(a\) and \(b\) are two whole numbers, then in general \(a – b\) is not equal to \((b – a)\).
3. If \(a\) is any whole number other than zero, then \(a – 0 = a\) but \(0 – a\) is not defined.
4. The subtraction of whole numbers is not associative. If \(a, b, c\) are three whole numbers, then in general, \(a – (b – c)\) is not equal to \((a – b) – c\).
5. If \(a, b\) and \(c\) are whole numbers such that \(a – b = c\), then \(b + c = a\).

Closure Property of Multiplication of Whole Numbers

If \(a\) and \(b\) are two whole numbers, then their product \(a \times b\) is also a whole number. In other words, if we multiply two whole numbers, we get a whole number.

Example: \(3 \times 2 = 6\). Here, \(3,2\) and \(6\) are whole numbers.

Commutative Property of Multiplication of Whole Numbers

The multiplication of whole numbers is commutative. In other words, if \(a\) and \(b\) are any two whole numbers, then, \(a \times b = b \times a\)

Example: \(9 \times 2 = 2 \times 9 = 18\)

Multiplicative Identity of a Whole Number

If \(a\) is any whole number, then \(a \times 1 = a = 1 \times a\). In other words, the product of any whole number and one is always the number itself.

Here, \(1\) is called the multiplicative identity.

Example: \(5 \times 1 = 5 = 1 \times 5\)

Associative Property of Multiplication of Whole Numbers

If \(a, b, c\) are any whole numbers, then \(\left({a + b} \right) + c = a + \left({b + c} \right)\). In other words, the multiplication of whole numbers is associative; that is, the product of three whole numbers does not change by changing the order.

Example: \((5 \times 3) \times 2 = 5 \times (3 \times 2) = 30\)

Distributive Property of Multiplication over Addition of Whole Numbers

If \(a, b, c\) are any three whole numbers, then, \(a \times (b + c) = a \times b + a \times c\) and \((b + c) \times a = b \times a + c \times a\). In other words, the multiplication of whole numbers distributes over their addition.

Example: \(3 \times (5 + 8) = 3 \times 5 + 3 \times 8 = 39\)

Division Properties of Whole Numbers

1. If \(a\) and \(b\) are whole numbers \((b \ne 0)\), then \(a \div b\) is not necessarily a whole number. In other words, whole numbers are not closed for division.
2. If \(a\) is any whole number, then, \(a \div 1 = a\).
Example: \(23 \div 1 = 23\)
3. If \(a\) is any whole number other than zero, then \(a \div a = 1\). In other words, any whole number other than zero divided by itself gives as the quotient.
Example: \(9 \div 9 = 1\)
4. Zero divided by any whole number gives the quotient as zero.
Example: \(0 \div 8 = 0\)
5. Let \(a, b, c\) be whole numbers and \(b \ne 0,c \ne 0\). If \(a \div b = c\), then \(b \times c = a\).
Example: \(12 \div 4 = 3 \Rightarrow 3 \times 4 = 12\)

Solved Examples – Properties of Whole Numbers

Question 1: Find the value of \(538 \times 8 + 538 \times 2\) using the suitable property.
Answer: Given, \(538 \times 8 + 538 \times 2\)
According to the distributive property of multiplication over addition, if \(a, b, c\) are any three whole numbers, then, \(a \times (b + c) = a \times b + a \times c\)
So, \(538 \times 8 + 538 \times 2 = 538 \times (8 + 2) = 538 \times 10 = 5380\)

Question 2: Determine the following product by suitable re-arrangement.
\(4 \times 4957 \times 25\)
Answer: We observe that \(4 \times 25 = 100\). So, we can rearrange the numbers to find the desired product as follows:
\(4 \times 4957 \times 25 = (4 \times 25) \times 4957 = 100 \times 4957 = 495700\)

Question 3: Umesh had ₹61000. He gave ₹8750 to Ashok, ₹12638 to Suresh and ₹35000 to Mahesh. How much money was left with him?
Answer: Total money with Umesh \(=₹61000\)
Money that was given to Ashok, Suresh and Mahesh \(=₹(8750+12638+35000)\)
\(=₹{(8750+35000)+12638}\)
\(=₹(43570+12638)\)
\(=₹56388\)
Therefore, money left with Umesh \(=₹(61000-56388)\)
\(=₹4612\)
Therefore, money left with Umesh \(=₹4612\)

Question 4: Determine the sum by suitable re-arrangement.
\(637 + 908 + 363\)
Answer: Given \(637 + 908 + 363\)
We observe that \(637 + 363 = 1000\), so we first add \(637\) and \(363\) as shown below.
\(637 + 908 + 363 = (637 + 363) + 908 = 1000 + 908 = 1908\)

Question 5: Determine the product of the greatest number of four digits and the greatest number of three digits.
Answer: We know that the greatest number of four digits \( = 9999\) and the greatest number of three digits \( = 999\)
Therefore, required product \( = 9999 \times 999\)
\( = 9999 \times (1000 – 1)\)
\( = 9999 \times 1000 – 9999 \times 1\)
\( = (10000 – 1) \times 1000 – (10000 – 1) \times 1\)
\( = 10000 \times 1000 – 1000 \times 1 – (10000 \times 1 – 1 \times 1)[\because(a – b) \times c = a \times c – b \times c]\)
\( = 1000000 – 1000 – 10000 + 1\)
\( = 10000001 – 11000 = 9989001\)

Therefore, the product of the greatest number of four digits and the greatest number of three digits is \(9989001\).

Summary

In this article, we have learnt the definition of whole numbers, properties of whole numbers. Also, we have known the commutative property of addition and multiplication of whole numbers, additive and multiplicative identity of whole numbers, associative property of addition and multiplication of whole numbers and solved some example problems.

FAQs

Q.1. What are whole numbers?
Ans: The natural numbers, along with zero, form the collection of whole numbers. That is, numbers \(0,1,2,3, \ldots \) are called whole numbers.

Q.2. What is the commutative property of addition in whole numbers?
Ans: If \(a\) and \(b\) are any two whole numbers, then \(a + b = b + a\). In other words, the sum of two whole numbers remains the same even if the order of whole numbers is changed.

Q.3. What is the associative property of addition in whole numbers?
Ans: If \(a, b, c\) are any three whole numbers, then \((a + b) + c = a + (b + c)\). In other words, the addition of whole numbers is associative.

Q.4. What is the commutative property of multiplication?
Ans: The multiplication of whole numbers is commutative. In other words, if \(a\) and \(b\) are any two whole numbers, then, \(a \times b = b \times a\)

Q.5. What is the distributive property of multiplication over addition?
Ans: If \(a, b, c\) are any three whole numbers, then, \(a \times (b + c) = a \times b + a \times c\) and \((b + c) \times a = b \times a + c \times a\).

Now you are provided with all the necessary information on the properties of whole numbers and we hope this detailed article is helpful to you. If you have any queries regarding this article, please ping us through the comment section below and we will get back to you as soon as possible.