Access Personalised Learning With Embibe Simple!
Download the Learning Outcomes App Today
Limits of Trigonometric Functions: Definition, Formulas, Examples
December 13, 2024
Symmetry: Know What is Symmetry in Geometry
December 2, 2024
Manipur Board Class 12 Syllabus 2025: Subject-wise PDF Download
November 17, 2024
RBSE Class 12 Updated Blueprint 2025: Download PDF
November 12, 2024
Karnataka PUC Result 2025: 1st/2nd PUC Result Date
November 12, 2024
ISC Class 11 Exam Books 2025
November 11, 2024
NCERT Books For Class 10 Science 2025: Download PDF
November 11, 2024
NCERT Books for Class 7
November 11, 2024
NCERT Books for Class 10 2025: Download PDF
November 11, 2024
Angle between Two Planes: Definition, Angle Bisectors of a Plane, Examples
November 10, 2024
A sequence is a set of values that repeat themselves according to a set of rules. The sequence describes the common relationship between the numbers in the provided collection. Numbers are the fundamental understanding of mathematical properties. Sequences can be found in a variety of numbers, including natural numbers, whole numbers, even and odd numbers, prime numbers, and so on.
By answering problems based on the formulas, the principles can be better understood. They are similar to sets, but the main difference is that individual terms in a sequence might appear multiple times in different positions. A sequence’s length is equal to the number of terms in it, and it might be finite or infinite.
You’ll learn about the different types of sequences, as well as examples, formulas, and other interesting information about the subject.
Practice Embibe’s Exclusive CBSE Sample Papers Based on New Guidelines:
Here at Embibe, you can get the CBSE Revised MCQ Mock Test 2021 for all topics. The MCQ Test offered by Embibe is curated based on revised CBSE Class Books, paper patterns and syllabus for the year 2021. This mock test series has a comprehensive selection of relevant questions and their solutions. Candidates in CBSE Board can take these mock tests to practise and find areas where they need to improve for their board exams.
A repeating arrangement of values with a certain rule is known as a sequence. A sequence is the list of objects or numbers in a particular order. The number sequence tells the common relationship between the given set of numbers. There are different types of sequences in our day-to-day life.
Let us discuss with an example. Keerthi and Soumya were walking along the road to meet their friend Mrudula. They observed the houses, which are numbered \(307, 309, 311, 313, ….\)
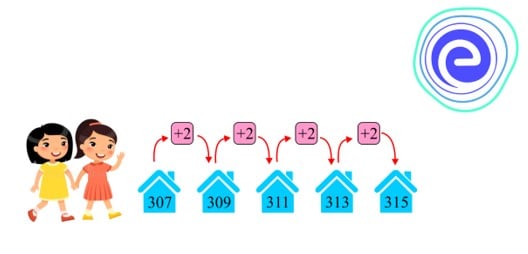
By observing these numbers, we can say that they are in ascending order. Thus, the above order tells the sequence, following specific rules (Each number is obtained by adding \(2\) to the previous number).
Therefore, the sequence is the series or list of objects or numbers with a particular rule.
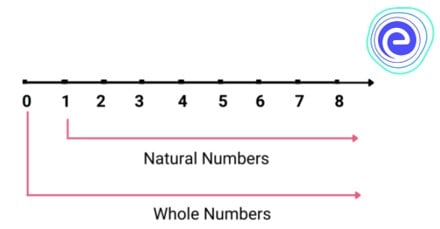
Numbers are a basic concept in mathematics. In our daily life, we use numbers for counting generally. All counting numbers are known as natural numbers. The natural numbers, along with zero, are called whole numbers. Thus, natural numbers start from one, and whole numbers start from zero.
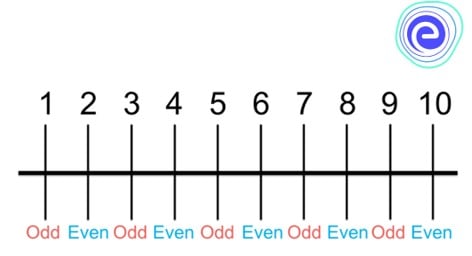
One of the basic patterns of the numbers is even and odd numbers. Numbers, which are exactly divisible by two \((2)\), are known as even numbers. Even numbers leave the remainder zero when it is divided by two.
Even numbers are generally in the form of \(2n\), where \(n=1, 2, 3, 4, ….\)
Example: \(2, 4, 6, 8, 10, 12, 14, 16, ….\)
The numbers, which are not divisible by two \((2)\), are known as odd numbers. They leave the remainder one when it is divided by two. Odd numbers are generally in the form of \(2n+1\), where \(n=0, 1, 2, 3, ….\)
Example: \(1, 3, 5, 7, 9, 11,13, 15…\)
One of the most used number sequences which we studied in our primary classes were prime and composite numbers. The numbers which have only two factors, such as one and themselves, are called prime numbers.
Example: \(2, 3, 5, 7, 11, 13, 17,…\)
\(2\) is the only even prime number and also the least prime number.
The numbers which have more than two factors are called composite numbers. \(4\) is the least composite number.
Example: \(4, 6, 8, 9, 10, 12, ….\)
In the above table, the blue colour marked tells the prime numbers, and the white colour-marked tells the composite number. The red colour marked number \((1)\) is neither prime nor composite.
Depending on the number of terms, there are two types of sequences
Let’s discuss them in detail.
A sequence is finite if the number of terms in the sequence is fixed. In other words, a set of fixed number which follows a certain rule is known as a finite sequence.
Example: Set of prime numbers below \(20\)
\(2, 3, 5, 7, 11, 13, 17,19\)
A sequence is infinite if the number of terms in the sequence is not fixed. In other words, a set of numbers that are not fixed and follows a certain rule is known as an infinite sequence.
Example: A set of natural numbers.
\(1, 2, 3, 4, 5, 6, 7, 8, ………\)
Sequences are the set of numbers, which are arranged in an order. In our primary classes, we studied ordering the objects, numbers according to their values.
There are two types of orders:
The numbers, written in the increasing order from the smallest to the largest, are in ascending order. In ascending order, the smallest number comes first and the largest number last.
Example: \(1, 2, 3, 4, 5, 6, …\)
The numbers, written in the decreasing order from the largest to the smallest, are in descending order. In descending order, the largest number comes first, and the smallest number comes last.
Example: \(100, 99, 98, 97, 96, …..\)
There are some special types of sequences in mathematics, such as arithmetic sequence, geometric sequence, Fibonacci sequence, harmonic sequence, triangular sequence, square and cube number sequences.
An arithmetic sequence is a series of numbers related to each other by a constant addition or subtraction. In an arithmetic sequence, each term is obtained by adding a constant number to the previous term (except the first term).
Here, the constant number is called a “common difference”, represented by d.
Let the first term of A.P is \({a_1}\), then
The second term is \({a_1} + d.\)
And, the third term is \({a_1} + d + d = {a_1} + 2d\)
The fourth term is \({a_1} + 2d + d = {a_1} + 3d\) and so on.
Example:
For series \(6,13, 20, 27, 34, …..\)
The first term is \(6\).
Here, each term is obtained by adding \(7\) to the previous term.
Thus, the common difference is \(7\).
The geometric sequence is a series of numbers related to each other by a constant multiplication or division.
In a geometric sequence, each term is obtained by multiplying a constant number to the previous term (Except the first term). Here, the constant number is called as “common ratio”, and it is represented by \(r\).
Let the first term of G.P is a, then
The second term is \(ar\).
And, the third term is \(ar \times r = a{r^2}\)
The fourth term is \(a{r^2} \times r = a{r^3}\) and so on.
Example:
for the series \(1, 2, 4, 8, 16, 32, ….\)
The first term is \(1\).
Each term is obtained by multiplying \(2\) to the previous term.
Thus, the common ratio is \(2\).
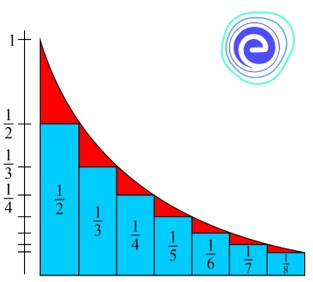
The harmonic sequence is the set of numbers in which all the numbers are reciprocal of the numbers of an arithmetic sequence.
For example: The reciprocals of natural numbers \((1, 2, 3, 4, 5, 6, 7, 8….)\) gives the harmonic sequence.
\(1,\frac{1}{2},\frac{1}{3} = \frac{1}{4},\frac{1}{5},\frac{1}{6} = \frac{1}{7},\frac{1}{8}, \cdots \)
A triangular number sequence is the set of numbers used to form some patterns in the form of an equilateral triangle. Dots represent the numbers in the triangle number patterns.
The numbers \(1, 3, 6, 10\), and so on are the triangular numbers, which form an equilateral triangle sequence.
https://exams-assets.embibe.com/exams/wp-content/uploads/2021/10/10202350/triangular-number-sequence1.jpgA square number is a number obtained by multiplying a number by itself. A square number sequence is the set of numbers that are forming in the form of a square.
The numbers \(1, 4, 9, 16, …\) and so on are the square number sequence, such that \({1^2} = 1,{2^2} = 4,{3^2} = 9\) and \({4^2} = 16\)
A cube number is obtained by multiplying a number by itself three times or multiplied by its square number. The cube number sequence is the set of numbers, which form the pattern in the cube form. A cube is a three-dimensional figure.
The numbers \(1, 8, 27, 64,\) …. And, so on are the cube numbers, such that \({1^3} = 1,{2^3} = 8,{3^3} = 27,{4^3} = 64\)
The Fibonacci sequence is the set of numbers in which each number is obtained by adding two terms preceding it. Thus, in the Fibonacci sequence, each number is the sum of its two previous numbers.
So, the sequence of numbers \(0, 1, 1, 2, 3, 5, 8, 13, 21, 34\), and so on is called the Fibonacci sequence.
November \(23rd\) is known as Fibanocci day, as it has the digits \(“1, 1, 2, 3″\), which is part of the sequence
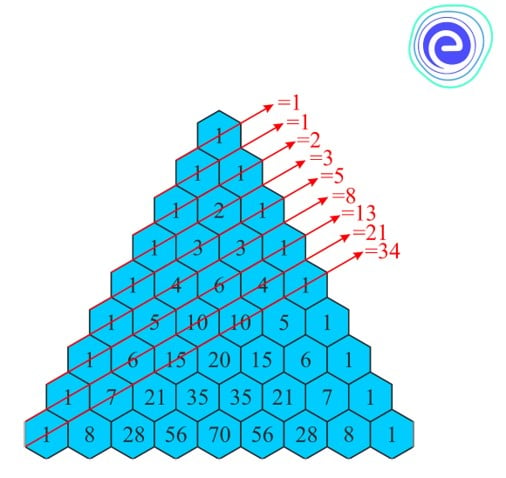
In the above figure, the red colour line drawn gives the Fibonacci number, the sum of the numbers on which it passes.
There are some formulas associated with the sequence and are listed below:
| Sequence | Formula |
| Arithmetic sequence | \({a_n} = a + (n – 1)d\) |
| Geometric sequence | \({a_n} = a \times {r^{n – 1}}\) |
| Harmonic sequence | \({a_n} = \frac{1}{{a + (n – 1)d}}\) |
| Fibonacci sequence | \({a_{n + 2}} = {a_n} + {a_{n + 1}}\) |
| Triangular sequence | \({a_n} = \sum\limits_{k = 1}^n k\) |
| Square number sequence | \({a_n} = {n^2}\) |
| Cube number sequence | \({a_n} = {n^3}\) |
Q.1. Find the missing number in the given Fibonacci sequence.\(5, 8, 13, ?, 34\)
Ans:
Given Fibonacci series is \(5, 8, 13,? 34\).
The Fibonacci sequence is the set of numbers in which each number is obtained by adding two terms preceding it.
The Fibonacci formulas \({a_{n + 2}} = {a_n} + {a_{n + 1}}\).
\(⟹4th\) term\(=3rd\) term\(+2nd\) term
So, the missing number in the sequence is \(8+13=21\).
Q.2. Observe the following number in the given sequence \(1, 3, 6, ….\)
Ans:
Given sequence is \(1, 3, 6, ….\)
We know that the given sequence of numbers is a triangular number sequence.
In which each number is obtained by forming the numbers in the form of an equilateral triangle.
The triangular number sequence is \(1, 1+2, 1+2+3, 1+2+3+4, …..\)
So, the following number in the given series is \(1+2+3+4=10\).
Q.3. What is the thirty-second term of the arithmetic sequence \(-12, -7, -2, 3, …\)?
Ans: The given sequence is \(-12, -7, -2, 3, …\)
From the above sequence,
\(a=-12\) (first term)
\(d=5\) (common difference)
The formula to be used: \({a_n} = a + d(n – 1)\)
\( \Rightarrow {a_n} = – 12 + 5(n – 1)\)
\( \Rightarrow {a_n} = – 12 + 5n – 5\)
\( \Rightarrow {a_n} = 5n – 17\)
So, the \(32\)nd term is:
\( \Rightarrow {a_{32}} = 5 \times 32 – 17\)
\( \Rightarrow {a_{32}} = 160 – 17\)
\( \Rightarrow {a_{32}} = 143\)
Hence, the \(32\)nd Term is \(143\).
Q.4. Find the \(10\)th term of the given geometric series \(4, 12, 36, 108, ……\)
Ans: Given series is \(4, 12, 36, 108, ……\)
From the above geometric series, \(a=4\) and the common ratio [r = \frac{{12}}{4} = 3\)
The \(10\)th terms of the geometric progression are found by using the formula: \({a_n} = a{r^{n – 1}}\).
\( \Rightarrow {a_{10}} = (4) \times {(3)^{10 – 1}}\)
\(\Rightarrow {a_{10}} = 4 \times {3^9}\)
\( \Rightarrow {a_{10}} = 4 \times 19683\)
\(\Rightarrow {a_{10}} = 78,732\)
Hence, the tenth term of the given series is \(78,732\).
Q.5. Find the missing value in the sequence given below: \(1, 4, 9, 16, 36, 49,….\)
Ans: Given sequence is \(1, 4, 9, 16,36, 49,….\)
The given sequence is known as the sequence of square numbers.
From the above sequence, we can write \({1^2},{2^2},{3^2},{4^2},{5^2},{6^2},{7^2}, \ldots \)
So, the missing number in the sequence is \({5^2} = 25\).
This article studied the sequence, which tells the common relationship between the given set of numbers or objects. We have studied different orders of the sequence (ascending or descending). A repeating arrangement of numbers with a certain rule known as a number sequence is also discussed with examples.
We discussed special sequences, such as arithmetic sequence, geometric sequence, harmonic sequence, triangular number sequence, square number sequence, cube number sequence, Fabinocci sequence, discussed with examples.
We have provided some frequently asked questions about sequences here:
Q.1. What is an arithmetic sequence?
Ans: An arithmetic sequence is a series of numbers related to each other by a constant addition or subtraction.
Q.2. What are the four types of sequences?
Ans: The four types of sequences are
1. Arithmetic sequence
2. Geometric sequence
3. Harmonic Sequence
4. Fibonacci sequence
Q.3. Explain the orders of the sequences.
Ans: There are two types of orders in the sequences are
1. Ascending or increasing order
2. Descending or decreasing order
Q.4. What is a sequence?
Ans: A repeating arrangement of values with a certain rule is known as a sequence. A sequence is the list of objects or numbers in a particular order.
Example: \(1, 2, 3, 4, 5, 6, 7, 8, 9, ….\)
Q.5. What is a geometric sequence?
Ans: The geometric sequence is a series of numbers related to each other by a constant multiplication or division.
We hope this detailed article on sequences proves helpful to you. If you have any doubts or queries on this topic, feel to ask us in the comment section we will assist you at the earliest.
Scan to Download the App 
JEE Main