Set Theoretic Approach: The concept of a set theory is foundational in modern mathematics. Today, practically every branch of Mathematics employs the use of this concept. Studying geometry, sequencing, probability, and other subjects involves understanding sets. Georg Cantor, a German mathematician, invented the theory of sets.

Set theory is a part of mathematical logic that analyses sets comprised of an informal grouping of objects. A set is a group of objects or a collection of objects. These objects are commonly referred to as set elements or members. The foundation of set theory is a binary relationship between an object \(x\) and a set \(A\). Set -theory is divided into several variants, each with its own set of rules and axioms. Continue reading this article to know more about Set Theoretic Approach, its definition, types, symbols, examples and more.

Definition of Sets and Representation

A set is defined as the collection of items (called members or elements). The notation \(x \in \,A\) is used when \(x\) is a member (or element) of \(A\), whereas \(x \notin \,A\) indicates that \(x\) is not a member of set \(A\).

A set is defined by a list of elements separated by commas within braces.

Example: The set of prime numbers less than \(10\) is written as \(A = \left\{ {2,3,5,7} \right\}\)

A set is a well-defined collection of things in Mathematics. An upper-case letter is used to name and represent sets. The elements that make up a set according to set theory can be anything, such as names, letters of the alphabet, numbers, shapes, and variables.

Cardinality of Set

A set’s cardinality is the number of elements in it. As a result, the cardinality of a finite set is always a natural number. \(\left| A \right|,{\text{ }}n\left( A \right)\) denotes the cardinality of a set \(A\). For instance, the set \(A = \left\{ {2,4,6,8} \right\}\) has four elements and cardinality of four.

Types of Sets

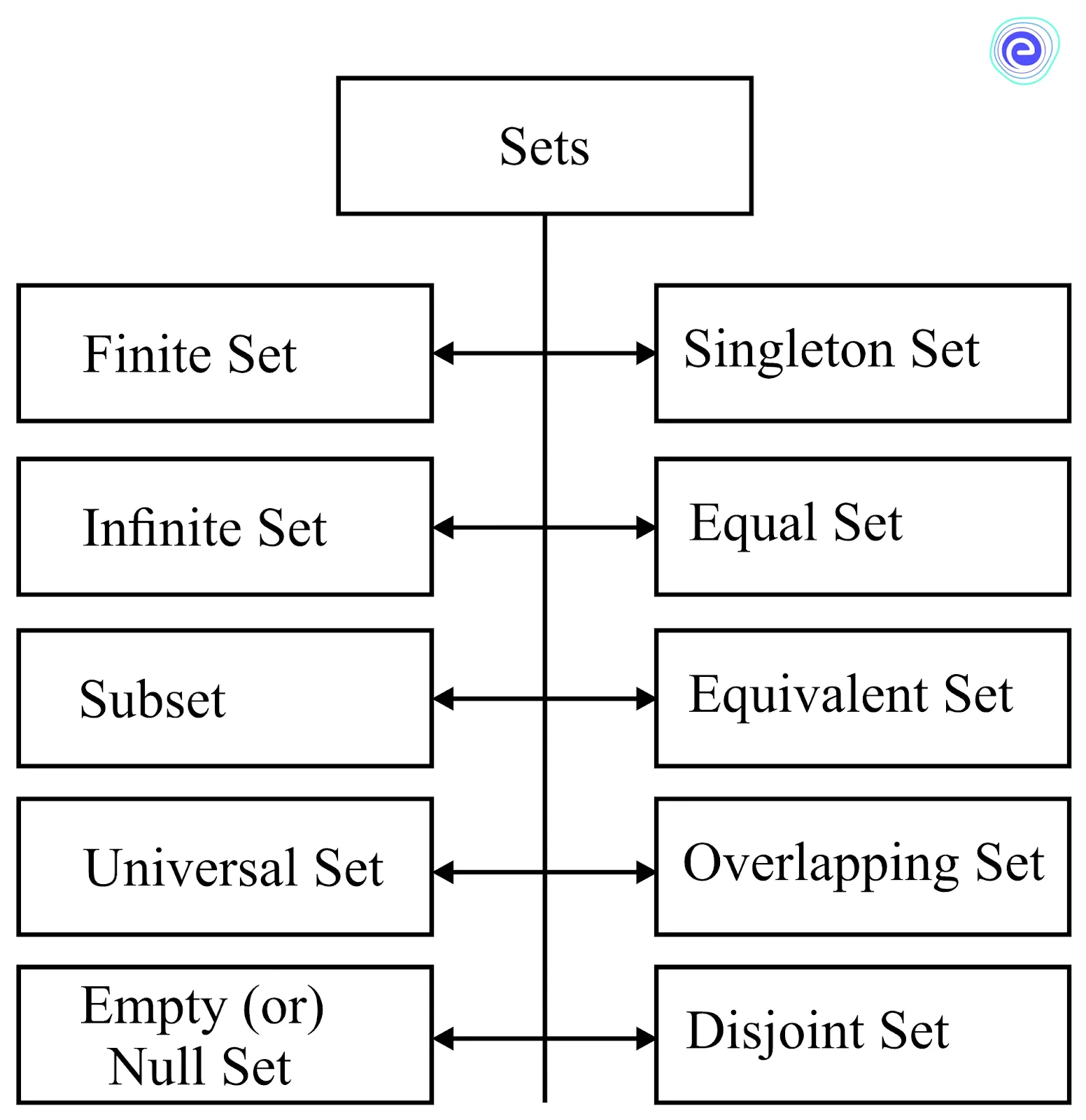
Sets can be categorised into many types based on their properties. Some are shown below.

• Finite Set
  A finite set is a set which contains a fixed or finite number of elements in it. 
  Example: \(A = \left\{ {2,3,4,5,6} \right\}\), hence, \(n\left( A \right) = 5\)
• Infinite Set
  A set which contains an infinite number of elements is called an infinite set.
  Example: Set of whole numbers, \(A = \left\{ {0,1,2,3,…..} \right\}\)
• Subset
  A set \(P\) is a subset of set \(Q\) if every element in \(X\) is also an element of set \(Q\). It is denoted as \(P \subseteq Q\).
  Example: If \(A\left\{ {2,4,6,8} \right\}\) and \(B = \left\{ {1,2,3,4,5,6,7,8,9} \right\},\), then \(B \subseteq B\).
• Universal Set
  The universal set defines the set that contains all of the elements of the sets under consideration. Universal set values change with sets. It is represented by the letter \( \cup \). For the same set, there may be many universal sets.
  Example: The universal set of two sets \(A=\left\{ {2,4,5} \right\}\) and \(B=\left\{ {1,3,5} \right\}\) is \( \cup  = \left\{ {1,2,3,4,5} \right\}\)
• Empty or Null Set
  There are no elements present in an empty set. It is denoted by the symbol \(\emptyset \) or using empty braces \(\left\{ {} \right\}\). An empty set is also finite since the number of elements is finite. The empty set is also known as a null set, and the cardinality of a null set is zero.
  Example: \(A = \left\{ {x:x < 0,\,x\,{\text{is}}\,{\text{a}}\,{\text{natural}}\,{\text{number}}} \right\}\)
• Singleton or Unit Set
  A singleton set, also called a unit set, has only one element. The term “singleton set” refers to a collection of only one item.
  Example: \(A = \left\{ {x:x\,{\text{is}}\,{\text{starting}}\,{\text{digit}}\,{\text{of}}\,{\text{a}}\,{\text{whole}}\,{\text{number}}} \right\}\)
• Equal Set
  Two sets are said to be equal sets if they contain the same elements.
  Example: Set \(A = \left\{ {2,4,6} \right\}\) and \(B=\left\{ {2,4,6} \right\}\) are said to be equal sets.
• Equivalent Set
  If the cardinalities of two sets are the same, they are called equivalent sets.
  Example: Two sets \(A = \left\{ {1,2,3} \right\}\) and \(B = \left\{ {5,6,7} \right\}\) are equivalent sets
• Overlapping Set
  Two sets are referred to as overlapping sets if they have at least one common element.
  Example: Two sets \(A = \left\{ {2,4,5} \right\}\) and \(B = \left\{ {1,3,5} \right\}\) are overlapping sets as they have only one common element.
• Disjoint Set
  Two sets and are called disjoint sets if they do not have even one element in common. 
  Example: Two sets \(A = \left\{ {1,2,3} \right\}\) and \(B = \left\{ {5,6,7} \right\}\) are disjoint sets, as they do not have any common element.

PRACTICE EXAM QUESTIONS AT EMBIBE

Symbols Used in Set Theoretic Approach

There are various symbols are used to represent the elements of a set.

The table below depicts several of these symbols and their meanings.

Symbols	Meaning
\( \cup \)	Universal set
\(n\left( x \right)\)	Cardinality of set \(X\)
\(b \in \,A\)	\(‘b’\) is an element of set \(A\)
\(a \notin \,B\)	\(‘a’\) is not an element of set \(B\)
\(\left\{ {} \right\}\)	Denotes a set
\(\emptyset \)	Null or empty set
\(A \cup B\)	Union set of set \(A\) and set \(B\)
\(A \cap B\)	Intersection set of set \(A\) and set \(B\)
\(A \subseteq B\)	Set \(A\) is a subset of set \(B\)
\(B \supseteq A\)	Set \(B\) is the superset of set \(A\)

Representation of Sets

Sets are represented mainly in two ways

• Set-Builder Method:
  Set builder notation in mathematics is a mathematical notation for describing a set by listing its elements or demonstrating the properties that its members must satisfy.
  Sets are written in the form of in set-builder notation as follows:
  \(\left\{ {y|\left( {{\text{properties}}\,{\text{of}}\,y} \right)} \right\}\,{\text{OR}}\,\left\{ {y:\,\left( {{\text{properties}}\,{\text{of}}\,y} \right)} \right\}\)
  Where \(y’\)s properties are replaced by the condition that completely describes the set’s elements. To separate the elements and properties, the symbol \(‘|’\) or \(‘:’\) is used. The symbols \(‘|’\) or \(‘:’\) are read as “such that,” and the complete set as “the set of all elements y” such that (properties of \(y\)). 
  Example: \(A = \left\{ {x:x < 10,\,\,{\text{is}}\,{\text{a}}\,{\text{prime}}\,{\text{number}}} \right\}\)
• Roaster Method:
  The elements of a set are represented in a row surrounded by curly brackets in roster notation, and if the set contains more than one element, every two elements are separated by commas. For example, if \(A\) is the set of the first ten natural numbers, then \(A = \left\{ {1,2,3,4,5,6,7,8,9,10} \right\}\)

Applications of Set Theoretic Approach

Mathematicians utilise set theory all the time. Many subfields of mathematics rely on it as a foundation. It is extremely useful in the field of statistics, especially in the field of probability. Many of the notions in probability are drawn from set theory.

A set is an abstract data type in Computer Science that stores an unordered collection of unique items. Sets are built-in data structures in many computer languages, akin to arrays or dictionaries.

Engineers utilise the set-theoretic approach mostly to ensure that the mathematics they use is treated precisely. Although the mathematics of logic circuits and set theory are not identical, they are highly comparable. Stochastic Differential Equations are used to analyse noise in circuit design.

Operations on Set Theory

There are various algebraic and arithmetic operations are implemented on the sets. The main four operations on sets such as the union of sets, the intersection of sets, the difference of sets and the symmetric difference of sets etc.

• Set Union:
  All the elements present in either \(A\) or \(B\) are present in the union of \(A\) and \(B\). It is represented as \(A \cup B\)
• Set Intersection:
  The set containing all the elements common to both sets is called the intersection of the given sets.
  for two sets, \(A\) and \(B\), the intersection is represented by \(A \cap B\)
• Set Difference:
  The set of elements that contains the elements of \(A\) but not \(B\) is the difference between the sets \(A\) and \(B\).
• Set Symmetric Difference:
  The set of elements which contains the elements of either set \(A\) or \(B\) but is not in their intersection is the symmetric difference of set \(A\) with respect to set \(B\).

Properties of Set Union and Intersection

The properties of set operations are listed below.

• Commutative Property
  \(A \cap B = B \cap A\)
  \(A \cup B = B \cup A\)
• Associative Property
  \(\left( {A \cup B} \right) \cup C = A \cup \left( {B \cup C} \right)\)
  \(\left( {A \cap B} \right) \cap C = A \cap \left( {B \cap C} \right)\)
• Distributive Property
  \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
  \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
• Property of Identity
  \(A \cup \emptyset  = A\)
  \(A \cap U = A\)
• Complement of Property
  \(A \cup {A^C} = U\)
  \(A \cap {A^C} = \emptyset \)
• Idempotent Property
  \(A \cap A = A\)
  \(A \cup A = A\)

Solved Examples on Set Theoretic Approach

Q.1. If \(U = \{ a,b,c,d,e,f\} ,A = \{ a,b,c\} ,B = \{ c,d,e,f\} ,C = \{ c,d,e\} \), find \(\left( {A \cap B} \right) \cup \left( {A \cap C} \right)\).
Solution:
\(A \cap B = \{ a,b,c\}  \cap \{ c,d,e,f\}  = \{ c\} \)
\(A \cap C = \{ a,b,c\}  \cap \{ c,d,e\}  = \{ c\} \)
\(\therefore (A \cap B) \cup (A \cap C) = \{ c\} \)

Q.2. Give three examples of a finite set.
Solution:
Finite set is a set which has a finite or fixed number of elements. Some of the examples of finite sets are
● Set of months in a year
● Set of days in a week
● Set of natural numbers less than \(20\)
● Set of integers greater than \(-2\) but less than \(3\)

Q.3. If \({\text{U = \{ 2,3,4,5,6,7,8,9,10,11\} , A = \{ 3,5,7,9,11\}}}\) and \(B = \left\{ {7,8,9,10,11} \right\}\), Then find \(\left( {A – B} \right)\).
Solution:
Given, \({\text{U = \{ 2,3,4,5,6,7,8,9,10,11\} , A = \{ 3,5,7,9,11\}}}\) and \(B = \left\{ {7,8,9,10,11} \right\}\)
\(A-B\)  is a set of members which belong to \(A\) but do not belong to \(B\)
\(A – B = \{ 3,5,7,9,11\}  – \{ 7,8,9,10,11\}  = \{ 3,5\} \)
\(\therefore A – B = \{ 3,5\} \)

Q.4. Express the set \(A = \left\{ {2,4,6,8,10,12,14} \right\}\) in set-builder form
Solution:
Given set is \(A = \left\{ {2,4,6,8,10,12,14} \right\}\)
Using sets notations, we can represent the given set \(A\) in set-builder form as,
\(A = \left\{ {x|x\,{\text{is}}\,{\text{an}}\,{\text{even}}\,{\text{natural}}\,{\text{number}}\,{\text{less}}\,{\text{than}}\,15} \right\}\)

Q.5. For the given sets \(A = \left\{ {1,2,3,4,5,6,7,8,9,10} \right\}\) and \(B = \left\{ {2,3,5,7} \right\}\) Find \(A \cap B\).
Solution:
Given \(A = \left\{ {1,2,3,4,5,6,7,8,9,10} \right\}\) and \(B = \left\{ {2,3,5,7} \right\}\)
\(A \cap B\) is the set that has the common elements in both the sets.
\(A \cap B = \{ 1,2,3,4,5,6,7,8,9,10\}  \cap \{ 2,3,5,7\}  = \{ 2,3,5,7\} \)

Summary

Georg Cantor established a solid theoretical foundation for it by recognising the importance of accurately described sets in the investigation of problems in symbolic logic and number theory. The study of set properties is known as set theory, and it is a branch of Mathematics. Set theory is helpful in understanding complex mathematical and philosophical ideas.

Its language and conceptions are useful when used in conjunction with other fields that borrow and alter them. Two of them are the operations of union and intersection. There are different types of sets based on the number of elements in it. The cardinality of a set is the number of elements in it. Sets are represented by set builder form and roaster method.

FAQs on Set Theoretic

Here are some frequently asked questions related to the set theoretic approach.

Q.1. What is the set theoretic approach?
Ans: The basis of the set theoretic approach is a binary relationship between an element \(x\) and a set \(A\). The notation \(x \in A\) is used when o is a member (or element) of \(A\). A set is described by a list of elements separated by commas, or by a characterising attribute of its elements within the brackets.

Q.2. Write the methods of representing the sets?
Ans: The set-builder form and roaster method are the methods of representing the sets.

Q.3. What is set theory?
Ans: Set theory is a mathematical concept that deals with well-defined groupings of objects known as members or elements of the set.

Q.4. What are the applications of set theory?
Ans: The sets used to investigate problems in logic and number theory. Practically every branch of Mathematics employs the use of this concept. The study of geometry, sequencing, probability, and other subjects involves understanding sets.

Q.5. What is the union of sets?
Ans: All of the elements present in either \(A\) or \(B\), or both sets, will be present in the union of \(A\) and \(B\), represented as \(A \cup B\).

ATTEMPT MOCK TESTS ON EMBIBE

We hope this article has provided you with the required information on Set Theoretic Approach. If you have any doubts regarding the same, do drop a comment in the section below and we will get back to you as soon as possible. For more such articles and info, please stay tuned to embibe.