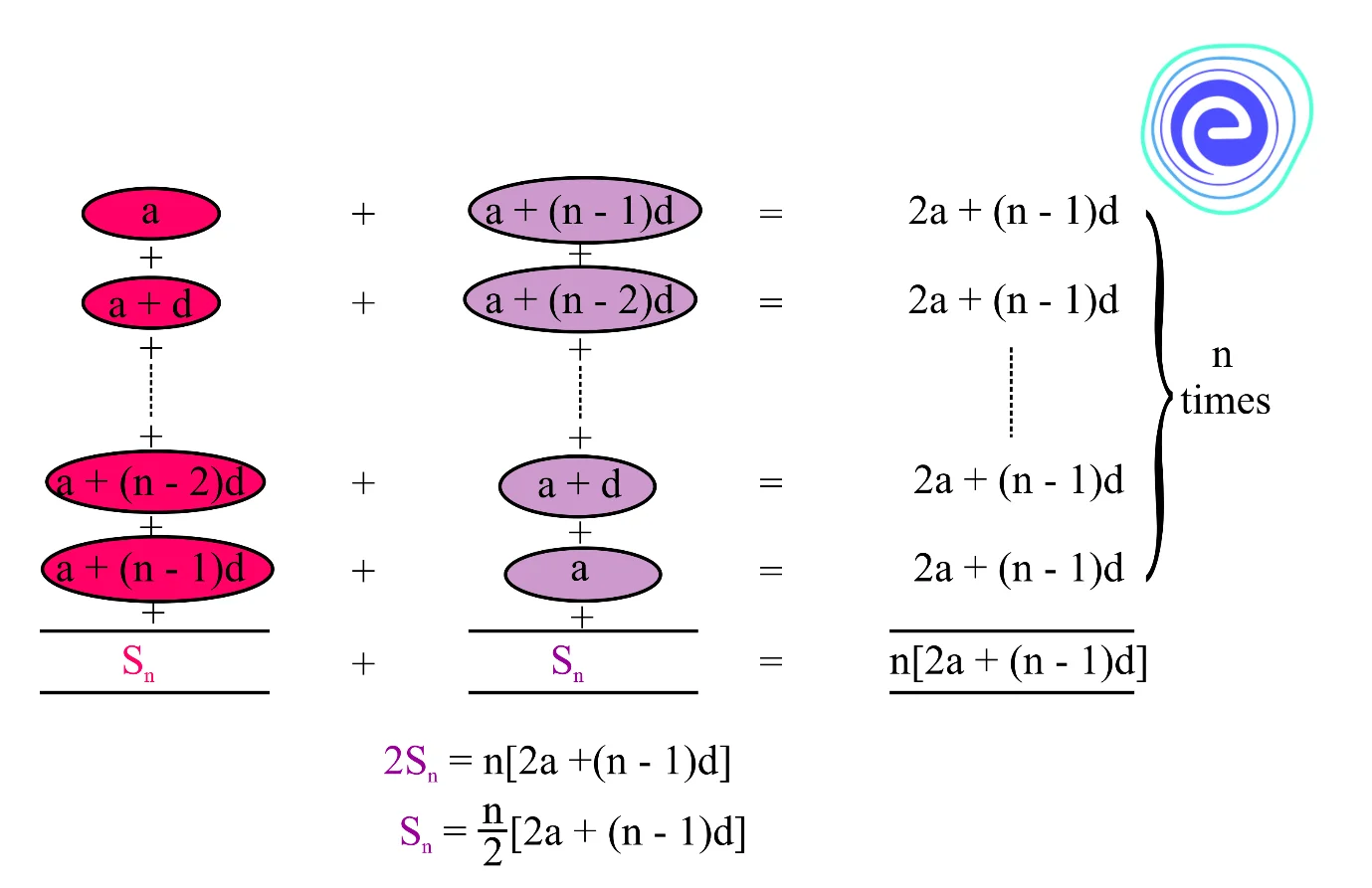Sum to n terms of Special Series: A sequence is a list of numbers in a specific order. Each number in a sequence is called a term. The sum of all the terms of a given sequence is called a series. A series with a countable number of terms is called a finite series, and that with an infinite number of terms is called an infinite series. The sum to \(n\) terms of a series is denoted by \({S_n}.\)

If the given sequence is \({t_{{1^\prime }}}{t_{{2^\prime }}}{t_{{3^\prime }}} \ldots {t_n}\) then the expression \({t_1} + {t_2} + {t_3} + \ldots + {t_n}\) is called the series corresponding to that sequence. Series can be written using sigma \(\left( \sum \right)\) notation. The \(\sum \) represents the summation of the terms. The concept of finite and infinite series has many applications in Mathematics, Computer Science, and Statistics.

Example: If the given sequence is: \({1^2},{2^2},{3^2},{4^2},{5^2},{6^2}, \ldots \ldots {n^2}\) 
Then,
Sum to two terms is: \({S_2} = {1^2} + {2^2}\)
Sum to three terms is: \({S_3} = {1^2} + {2^2} + {3^2}\)  
Sum to four terms is: \({S_4} = {1^2} + {2^2} + {3^2} + {4^2}\)
Sum to n terms is: \({S_n} = {1^2} + {2^2} + {3^2} + {4^2} + \ldots + {n^2}\)

Learn Everything About Mean and Median Here

Different Types of Series

Arithmetic Series

The sum of a definite number of terms in an arithmetic sequence is called an arithmetic series. In an arithmetic series, the difference between two consecutive terms is always equal. This difference is called the common difference, and it is denoted by \(d.\)

The general form of an arithmetic series is:

\({S_n} = a + (a + d) + (a + 2d) + (a + 3d) + \ldots + (a + (n – 1)d)\)

Sigma notation of an arithmetic series is:

\({S_n} = \sum\limits_{k = 1}^n a + (k – 1)d\)

Here, 

\(a\) is the first term

\(d\) is the common difference

\(n\) is the total number of terms

Sum to \(n\) Terms of an Arithmetic Series

The formula used to calculate the sum of n terms of an arithmetic series is:

\({S_n} = \frac{n}{2}[2a + (n – 1)d]\)

Proof: 

Arithmetic series:

\({S_n} = a + (a + d) + (a + 2d) + \ldots + (a + (n – 2)d) + (a + (n – 1)d)\)

By writing the terms of this equation in the reverse order, we get:     

\({S_n} = (a + (n – 1)d) + (a + (n – 2)d) + \ldots (a + 2d) + (a + d) + a\)

Now adding the corresponding terms of the above two equations:

Example 1: 

Find the sum of the series \(1+4+7+10+⋯\) to \(22\) terms.

Ans:     

Sum to \(n\) terms of an arithmetic series: \({S_n} = \frac{n}{2}[2a + (n – 1)d]\)

Here, 

\(a = 1\)

\(d = 3\)

\(n = 22\)

\({S_n} = \frac{n}{2}[2a + (n – 1)d]\)

\(\therefore {S_{22}} = \frac{{22}}{2}[2(1) + (22 – 1)3]\)

\({S_{22}} = 11[2 + (21)3]\)

\({S_{22}} = 11[2 + 63]\)

\({S_{22}} = 11[65]\)

\({S_{22}} = 715\)

Example 2: 

Find the value of \(n\) if \(25+22+19+⋯\) to \(n\) terms\(=116\)

Ans:

Sum to \(n\) terms of an arithmetic series: \({S_n} = \frac{n}{2}[2a + (n – 1)d]\)

Here, 

\(a = 25\)

\(d = 22 – 25 =\, – 3\)

\({S_n} = 116\)

\(\therefore 116 = \frac{n}{2}[2(25) + (n – 1)( – 3)]\)

\(232 = n[50 – 3n + 3]\)

\(232 = 53n – 3{n^2}\)

\(3{n^2} – 53n + 232 = 0\)

\((3n – 29)(n – 8) = 0\)

\(3n – 29 = 0\) or \((n – 8) = 0\)

\(n = \frac{{29}}{3}\) or \(n = 8\)

but \(n \in N,\,\therefore n = 8\)

Geometric Series

The sum of a definite number of terms in a geometric sequence is called a geometric series. In a geometric series, the ratio of two consecutive terms is always equal. This ratio is called the common ratio, and it is denoted by \(r.\)

The general form of a geometric series is:

\({S_n} = a + (ar) + \left( {a{r^2}} \right) + \left( {a{r^3}} \right) + \ldots \ldots … + \left( {a{r^{n – 1}}} \right)\)

The sigma notation of a geometric series is:

\({S_n} = \sum\limits_{k = 1}^n a {r^{k – 1}}\)

Here, 

\(a\) is the first term,

\(r\) is the common ratio,

Sum to \(n\) Terms of a Geometric Series 

\(n\) is the total number of terms.

The formula used to calculate the sum of \(n\) terms of a geometric series is:

\({S_n} = \frac{{a\left( {{r^n} – 1} \right)}}{{(r – 1)}}\)

Proof: 

Geometric series: \({S_n} = a + (ar) + \left( {a{r^2}} \right) + \left( {a{r^3}} \right) + \ldots \ldots + \left( {a{r^{n – 1}}} \right) \to ({\rm{i}})\)

Multiplying the above equation with r on both the sides, we get:

\(r{S_n} = (ar) + \left( {a{r^2}} \right) + \left( {a{r^3}} \right) + \ldots …. + \left( {a{r^{n – 1}}} \right) + a{r^n} \to {\rm{(ii)}}\)

Subtracting above two equations: (ii) – (i), we get: 

\(r{S_n} – {S_n} = a{r^n} – a\)

\({S_n}(r – 1) = a\left( {{r^n} – 1} \right)\)

\({S_n} = \frac{{a\left( {{r^n} – 1} \right)}}{{(r – 1)}}\)

Example 1:

Find the sum of first \(n\) terms and the sum of first \(5\) terms of the geometric

series \(1 + \frac{2}{3} + \frac{4}{9} + \ldots \)

Ans:

Sum of \(n\) terms of a geometric series: \({S_n} = \frac{{a\left( {{r^n} – 1} \right)}}{{(r – 1)}}\)

Here, 

\(a=1\)

\(r = \frac{2}{3}\)

\(\therefore {S_n} = \frac{{1 \cdot \left[ {{{\left( {\frac{2}{3}} \right)}^n} – 1} \right]}}{{\frac{2}{3} – 1}}\)

\( = 3\left[ {1 – {{\left( {\frac{2}{3}} \right)}^n}} \right]\)

Sum of \(5\) terms of the series: \(:{S_5} = 3\left[ {1 – {{\left( {\frac{2}{3}} \right)}^5}} \right]\)

\( = 3 \times \frac{{211}}{{243}}\)

\({S_5} = \frac{{211}}{{81}}\)

\({S_5} = 2\frac{{49}}{{81}}\)

Example 3:

Find the sum of the series \(7+77+777+7777+…\) to \(n\) terms.

Ans:

First, we need to write it as a geometric series:

\({S_n} = 7 + 77 + 777 + 7777 + \ldots {\rm{to}}\,n\,{\rm{terms}}\)

\( = \frac{7}{9}[9 + 99 + 999 + 9999 + \ldots {\rm{to}}\,n\,{\rm{terms}}]\)

\( = \frac{7}{9}\left[ {(10 – 1) + \left( {{{10}^2} – 1} \right) + \left( {{{10}^3} – 1} \right) + \left( {{{10}^4} – 1} \right) + \ldots n} \right.\,{\rm{terms}}]\)

\( = \frac{7}{9}\left[ {\left( {10 + {{10}^2} + {{10}^3} + \cdots n} \right.} \right.\,{\rm{terms}}) – (1 + 1 + 1 + \ldots n\,{\rm{terms}}\left. ) \right]\)

\( = \frac{7}{9}\left[ {\frac{{10\left( {{{10}^n} – 1} \right)}}{{10 – 1}} – n} \right]\)

\({S_n} = \frac{7}{9}\left[ {\frac{{10\left( {{{10}^n} – 1} \right)}}{9} – n} \right]\)

Arithmetico-Geometric Series

A sequence in which each term is the product of the corresponding terms of an arithmetic sequence and geometric sequence is called an arithmetico-geometric sequence. The sum of all the terms of this sequence is called arithmetico-geometric series.
The general form of an arithmetico-geometric series is:
\(a + \left( {a + d} \right)r + \left( {a + 2d} \right){r^2} + … + \left( {a + \left( {n – 1} \right)d} \right){r^{n – 1}}\)

Sum to \(n\) Terms of an Arithmetico-Geometric Series: 

The arithmetico-geometric series is represented as:

\({S_n} = a + (a + d)r + (a + 2d){r^2} + \cdots + (a + (n – 1)d){r^{n – 1}}\)

The formula used to calculate the sum of \(n\) terms of an arithmetico-geometric series is:

\({S_n} = \frac{a}{{(1 – r)}} + \frac{{dr\left( {1 – {r^{n – 1}}} \right)}}{{{{(1 – r)}^2}}} + \frac{{(a + (n – 1)d){r^n}}}{{1 – r}}\)

Proof:

Arithmetico-geometric series:

\({S_n} = a + (a + d)r + (a + 2d){r^2} + \ldots + [a + (n – 1)d]{r^{n – 1}}\)

\(\therefore {S_n} = a + ar + dr + a{r^2} + 2d{r^2} + \ldots + a{r^{n – 1}} + (n – 1)d{r^{n – 1}}…..\left( {\rm{i}} \right)\)

\(\therefore r{S_n} = ar + a{r^2} + d{r^2} + a{r^3} + 2d{r^3} + \ldots + a{r^n} + (n – 1)d{r^n}……\left( {{\rm{ii}}} \right)\)

Subtracting \(\left( {{\rm{ii}}} \right)\) from \(\left( {\rm{i}} \right)\) we get

\({S_n} – r{S_n} = a + dr + d{r^2} + \ldots d{r^{n – 1}} – a{r^n} – (n – 1)d{r^n}\)

\(\therefore {S_n}(1 – r) = a + dr + d{r^2} + \ldots + d{r^{n – 1}} – [a + n(n – 1)d]{r^n}\)

\({S_n}(1 – r) = a + dr\left( {\frac{{1 – {r^{n – 1}}}}{{(1 – r)}}} \right) – [a + (n – 1)d]{r^n}\)

\({S_n} = \frac{a}{{1 – r}} + \frac{{dr\left( {1 – {r^{n – 1}}} \right)}}{{{{(1 – r)}^2}}} – \frac{{[a + (n – 1)d]{r^n}}}{{1 – r}}\)

Example 5: 

Find the sum of first \(n\) terms of the series  \(1 + 4 + 12 + 32 + 80 + 192 + \ldots \)

Ans:

Given series can be written as \(1 \times 1 + 2 \times 2 + 3 \times 4 + 4 \times 8 + 5 \times 16 + \ldots \)

Sum of \(n\) terms of arithmetic-geometric series:

\({S_n} = \frac{a}{{(1 – r)}} + \frac{{dr\left( {1 – {r^{n – 1}}} \right)}}{{{{(1 – r)}^2}}} + \frac{{(a + (n – 1)d){r^n}}}{{1 – r}}\)

Here,  

\(a=1\)

\(d=1\)

\(r=2\)

Substituting the values of \(a, d, r\) we get: 

\({S_n} = \frac{1}{{1 – 2}} + 1 \times 2\frac{{\left( {1 – {2^{n – 1}}} \right)}}{{{{(1 – 2)}^2}}} – \frac{{[1 + (n – 1)1]{2^n}}}{{1 – 2}}\)

\({S_n} = \frac{1}{{ – 1}} + 2\left( {1 – {2^{n – 1}}} \right) + n \times {2^n}\)

\({S_n} = \, – 1 + 2 – {2^n} + n{2^n}\)

\({S_n} = 1 – {2^n} + n{2^n}\)

\({S_n} = 1 – {2^n}(1 – n) = 1 + (n – 1){2^n}\)

Special Series

Special series are those which have special use in evaluating summation of the other types of series. 

Some special series are listed below:

(i) Sum of the first \(n\) natural numbers\( = 1 + 2 + 3 + \ldots + n\)

\({S_n} = \sum\limits_{k = 1}^n k = 1 + 2 + 3 + \cdots + n\)

(ii) Sum of squares of the first \(n\) natural numbers\( = {1^2} + {2^2} + {3^2} + \ldots + {n^2}\)

\({S_n} = \sum\limits_{k = 1}^n {{k^2}} = {1^2} + {2^2} + {3^2} + \ldots + {n^2}\)

(iii) Sum of cubes of the first \(n\) natural numbers\( = {1^3} + {2^3} + {3^3} + \ldots + {n^3}\)

\({S_n} = \sum\limits_{k = 1}^n {{k^3}} = {1^3} + {2^3} + {3^3} + \ldots + {n^3}\)

Sum to \(n\) Terms of Special Series

(i) Sum of the First \(n\) Natural Numbers

The formula used to calculate the first \(n\) natural numbers:

\({S_n} = \frac{{n(n + 1)}}{2}\)

Proof:

We need to find the sum of the first \(n\) natural numbers. 

Here,

\(a=1\)

\(d=1\)

The sum to \(n\) terms of an arithmetic series is given by:

\({S_n} = \frac{n}{2}[2a + (n – 1)d]\)

\({S_n} = \frac{n}{2}[2(1) + (n – 1)1]\)

\({S_n} = \frac{{n(n + 1)}}{2}\)

(ii) Sum of the Squares of the First \(n\) Natural Numbers

The formula used to calculate the squares of first \(n\) natural numbers:

\({S_n} = \frac{{n(n + 1)(2n + 1)}}{6}\)

Proof:

Sum of the squares of first \(n\) natural numbers: \({S_n} = {1^2} + {2^2} + {3^2} + \ldots + {n^2}\)

Now, consider the identity, \({k^3} – {(k – 1)^3} = 3{k^2} – 3k + 1\)

Substituting \(k = 1,2 \ldots ,n\)  successively, we obtain

\({1^3} – {0^3} = 3{(1)^2} – 3(1) + 1\)

\({2^3} – {1^3} = 3{(2)^2} – 3(2) + 1\)

\({3^3} – {2^3} = 3{(3)^2} – 3(3) + 1\)

\({n^3} – {(n – 1)^3} = 3{(n)^2} – 3(n) + 1\)

Adding both sides of all these equations, we get

\({n^3} – {0^3} = 3\left( {{1^2} + {2^2} + {3^2} + \ldots + {n^2}} \right) – 3(1 + 2 + 3 + \ldots + n) + n\)

\({n^3} = 3\sum\limits_{k = 1}^n {{k^2}} – 3\sum\limits_{k = 1}^n k + n\)

We know that,

\(\sum\limits_{k = 1}^n k = 1 + 2 + 3 + \cdots + n = \frac{{n(n + 1)}}{2}\)

So now,

\({S_n} = \sum\limits_{k = 1}^n {{k^2}} \)

\( = \frac{1}{3}\left[ {{n^3} + \frac{{3n(n + 1)}}{2} – n} \right]\)

\({S_n} = \frac{1}{6}\left( {2{n^3} + 3{n^2} + n} \right)\)

\({S_n} = \frac{{n(n + 1)(2n + 1)}}{6}\)

(iii) Sum of the Cubes of the First \(n\) Natural Numbers

The formula used to calculate the cubes of first \(n\) natural numbers:

\({S_n} = {\left[ {\frac{{n(n + 1)}}{2}} \right]^2}\)

Proof:

Sum of cubes of natural numbers: \({S_n} = {1^3} + {2^3} + {3^3} + \ldots + {n^3}\)

Consider the identity, \({(k + 1)^4} – {k^4} = 4{k^3} + 6{k^2} + 4k + 1\)

By substituting \(k\) with \(1, 2,3, …n,\) we get:

\({2^4} – {1^4} = 4{(1)^3} + 6{(1)^2} + 4(1) + 1\)

\({3^4} – {2^4} = 4{(2)^3} + 6{(2)^2} + 4(2) + 1\)

\({4^4} – {3^4} = 4{(3)^3} + 6{(3)^2} + 4(3) + 1\)

\({(n – 1)^4} – {(n – 2)^4} = 4{(n – 2)^3} + 6{(n – 2)^2} + 4(n – 2) + 1\)

\({n^4} – {(n – 1)^4} = 4{(n – 1)^3} + 6{(n – 1)^2} + 4(n – 1) + 1\)

\({(n + 1)^4} – {n^4} = 4{n^3} + 6{n^2} + 4n + 1\)

Adding both sides of all these equations, we get

\({(n + 1)^4} – {1^4} = 4\left( {{1^3} + {2^3} + {3^3} + \ldots + {n^3}} \right) + 6\left( {{1^2} + {2^2} + {3^2} + \ldots + {n^2}} \right) +\)
\( 4(1 + 2 + 3 + \ldots + n) + n\)

\({(n + 1)^4} – {1^4} = 4\sum\limits_{k = 1}^n {{k^3}} + 6\sum\limits_{k = 1}^n {{k^2}} + 4\sum\limits_{k = 1}^n k + n \to \left( 1 \right)\)

We know that,

\(\sum\limits_{k = 1}^n k = \frac{{n(n + 1)}}{2}\)

and,

\({S_n} = \sum\limits_{k = 1}^n {{k^2}} = \frac{{n(n + 1)(2n + 1)}}{6}\)

Substituting these values in equation \((1)\) we obtain:

\(4\sum\limits_{k = 1}^n {{k^3}} = {n^4} + 4{n^3} + 6{n^2} + 4n – \frac{{6n(n + 1)(2n + 1)}}{6} – \frac{{4n(n + 1)}}{2} – n\)

\(4{S_n} = {n^4} + 4{n^3} + 6{n^2} + 4n – n\left( {2{n^2} + 3n + 1} \right) – 2n(n + 1) – n\)

\(4{S_n} = {n^4} + 2{n^3} + {n^2}\)

\(4{S_n} = {n^2}{(n + 1)^2}\)

\({S_n} = {\left[ {\frac{{n(n + 1)}}{2}} \right]^2}\)

Properties of Summation

i)  Summation can be applied by bringing the constant term outside the summation operator.

\(\sum\limits_{r – 1}^n K {t_r} = K\sum\limits_{r = 1}^n {{t_{{r^\prime }}}} K \ne 0\)

ii) Summation can be applied to two terms in addition separately.

\(\sum\limits_{r = 1}^n {\left( {{a_r} + {b_r}} \right)} = \sum\limits_{r = 1}^n {{a_r}} + \sum\limits_{r = 1}^n {{b_r}} \)

iii) Summation of \(1\) added \(n\) times is \(n.\)

\(\sum\limits_1^n 1 = n\)

iv) Summation of \(K\) added \(n\) times is \(Kn.\)

\(\sum\limits_1^n K = K\sum\limits_1^n 1 = Kn, \ldots ,K \ne 0\)

Solved Problems on Sum to n Terms of Special Series

Q.1. Find the sum of the first 50 natural numbers.
Ans: Sum of the first \(50\) natural numbers\(5 = 1 + 2 + 3 + \ldots + 48 + 49 + 50\)
The formula used to calculate the first \(n\) natural numbers:
\({S_n} = \frac{{n(n + 1)}}{2}\)
Here, \(n=50\)
\({S_{50}} = \frac{{50(50 + 1)}}{2}\)
\( = \frac{{50 \times 51}}{2}\)
\(=1275\)

Q.2. Evaluate: \({3^2} + {4^2} + {5^2} + \cdots + {29^2}\)
Ans: The formula used to calculate the first n natural numbers:
\({S_n} = \frac{{n(n + 1)}}{2}\)
Given: \({3^2} + {4^2} + {5^2} + \cdots + {29^2}\)
This can be written as,
\( = \left( {{1^2} + {2^2} + {3^2} + \ldots + {{29}^2}} \right) – \left( {{1^2} + {2^2}} \right)\)
\( = \sum\limits_{r = 1}^{29} {{r^2}} – (1 + 4)\)
\( = \sum\limits_{r = 1}^{29} {{r^2}} – \left( 5 \right)\)
We know that,
\(\sum\limits_{r = 1}^n {{r^2}} = \frac{{n(n + 1)(2n + 1)}}{6}\)
Here \( = \frac{{29(29 + 1)(58 + 1)}}{6} – 5\)
\( = \frac{{29 \times 30 \times 59}}{6} – 5\)
\( = 5(29 \times 59 – 1)\)
\( = 5(1711 – 1)\)
\( = 5(1710)\)
\( = 8550\)

Q.3. Find the sum to n terms of the series: \(5+11+19+29+41….\)
Ans: Given:
\({S_n} = 5 + 11 + 19 + 29 + \ldots + {a_{n – 1}} + {a_n}\)
\({S_n} = 5 + 11 + 19 + \ldots + {a_{n – 2}} + {a_{n – 1}} + {a_n}\)
on subtracting, we get:
\(0 = 5 + [6 + 8 + 10 + 12 + \ldots (n – 1)\,{\rm{terms}}] – {a_n}\)
or
\({a_n} = 5 + \frac{{(n – 1)[12 + (n – 2) \times 2]}}{2}\)
\( = 5 + (n – 1)(n + 4)\)
\(\therefore {a_n} = {n^2} + 3n + 1\)
Hence,
\({S_n} = \sum\limits_{k = 1}^n {{a_k}} = \sum\limits_{k = 1}^n {\left( {{K^2} + 3k + 1} \right)} = \sum\limits_{K = 1}^n {{k^2}} + 3\sum\limits_1^n k + n\)
We know that,
\(\sum\limits_{k = 1}^n k = \frac{{n(n + 1)}}{2}\)
and,
\(\sum\limits_{k = 1}^n {{k^2}} = \frac{{n(n + 1)(2n + 1)}}{6}\)
So now,
\({S_n} = \frac{{n(n + 1)(2n + 1)}}{6} + \frac{{3n(n + 1)}}{2} + n\)
\(\therefore {S_n} = \frac{{n(n + 2)(n + 4)}}{3}\)

Q.4. Find the sum to n terms of the series whose \({n^{{\rm{th}}}}\) term is \(n\left( {n + 3} \right).\)
Ans: Given: \({a_n} = n(n + 3) = {n^2} + 3n\)
Thus, the sum to n terms is given by,
\({S_n} = \sum\limits_{k = 1}^n {{a_k}} = \sum\limits_{k = 1}^n {{k^2}} + 3\sum\limits_{k = 1}^n k \)
\( = \frac{{n(n + 1)(2n + 1)}}{6} + \frac{{3n(n + 1)}}{2}\)
\({S_n} = \frac{{n(n + 1)(n + 5)}}{3}\)

Q.5. Find the sum to n terms of the series: \({100^2} – {99^2} + {98^2} – {97^2} + \ldots + {2^2} – {1^2}\)
Ans: Given: \({100^2} – {99^2} + {98^2} – {97^2} + \ldots + {2^2} – {1^2}\)
\( = \left( {{{100}^2} + {{98}^2} + {{96}^2} + \ldots + {2^2}} \right) – \left( {{{99}^2} + {{97}^2} + {{95}^2} + \ldots . + {1^2}} \right)\)
\( = \sum\limits_{r = 1}^{50} {{{(2r)}^2}} – \sum\limits_{r = 1}^{50} {{{(2r – 1)}^2}} \)
\( = \sum\limits_{r = 1}^{50} {\left( {4{r^2} – 4{r^2} + 4r – 1} \right)} \)
\( = \sum\limits_{r = 1}^{50} {(4r – 1)} \)
\( = \sum\limits_{r = 1}^{50} 4 r – \sum\limits_{r = 1}^{50} 1 \)
\( = 4\sum\limits_{r = 1}^{50} r – \sum\limits_{r = 1}^{50} 1 \)
we know that,
\(\sum\limits_{k = 1}^n k = \frac{{n(n + 1)}}{2}\)
and
\(\sum\limits_{r = 1}^n 1 = n\)
\( = 4 \times \frac{{50(50 + 1)}}{2} – 50\)
\( = 2 \times 50 \times 51 – 50\)
\( = 50(2 \times 51 – 1)\)
\( = 50(101)\)
\( = 5050\)

Q.6. Find the sum to n terms of the series: \(1 \times 5 + 3 \times 7 + 5 \times 9 + 7 \times 11 + \ldots \)
Ans: Let \({S_n} = 1 \times 5 + 3 \times 7 + 5 \times 9 + 7 \times 11 + \ldots \)
\(\therefore {S_n} = \sum\limits_{r = 1}^n {(2r – 1)} (2r + 3)\)
\( = \sum\limits_{r = 1}^n {\left( {4{r^2} + 4r – 3} \right)} \)
\( = 4\sum\limits_{r = 1}^n {{r^2}} + 4\sum\limits_{r = 1}^n r – \sum\limits_{r = 1}^n 3 \)
we know that,
\(\sum\limits_{r = 1}^n {{r^2}} = \frac{{n(n + 1)(2n + 1)}}{6}\)
\(\sum\limits_{r = 1}^n r = \frac{{n(n + 1)}}{2}\)
and
\(\sum\limits_{r = 1}^n k = kn\)
So,
\({S_n} = 4\frac{{n(n + 1)(2n + 1}}{6} + 4\frac{{n(n + 1)}}{2} – 3n\)
\( = n\left[ {\frac{{2(n + 1)(2n + 1}}{3}} \right] + 2n(n + 1) – 3n\)
\( = \frac{n}{3}\left[ {2\left( {2{n^2} + n + 2n + 1} \right) + 6(n + 1) – 9} \right]\)
\( = \frac{n}{3}\left[ {\left( {4{n^2} + 6n + 2} \right) + 6n – 3} \right]\)
\( = \frac{n}{3}\left( {4{n^2} + 12n – 1} \right)\)

Summary

This article explains how a series is different from a sequence and about how they are similar too. A few common types of series are discussed, such as arithmetic series and geometric series with solved problems. It also shows how to employ the formulas to calculate the values of different special series. It also explains about properties of summation and sum of the first \(n\) natural numbers, the sum of the squares of the first \(n\) natural numbers, the sum of the cubes of the first \(n\) natural numbers and finding sum to \(n\) terms of given series using these properties and formulas.

FAQs

Q.1. What is the sum of n terms of series?
Ans: The sum of \(n\) terms of series is the addition of all the terms from \({1^{{\rm{st}}}}\) term to \({n^{{\rm{th}}}}\) term of a given series.
For example, the sum of \(n\) terms of an arithmetic series is given by:
\({S_n} = \frac{n}{2}[2a + (n – 1)d]\)

Q.2. How do you find the sum of \(n\) terms of special series?
Ans: First, find the general term or \({n^{{\rm{th}}}}\) of the given series and then by applying the summation to this \({n^{{\rm{th}}}}\) term and simplifying, we get the sum of \(n\) terms of special series.

Q.3. What is the sum of the first \(n\) natural numbers?
Ans: The sum of the first \(n\) natural numbers is given by:
\({S_n} = \sum\limits_{k = 1}^n k = 1 + 2 + 3 + \cdots + n = \frac{{n(n + 1)}}{2}\)

Q.4. What is the sum of the squares of the first n natural numbers?
Ans: The sum of the squares of the first \(n\) natural numbers is given by:
\({S_n} = \sum\limits_{k = 1}^n {{k^2}} = {1^2} + {2^2} + {3^2} + \ldots + {n^2} = \frac{{n(n + 1)(2n + 1)}}{6}\)

Q.5. What is the sum of geometric series?
Ans: To find the sum to \(n\) terms of a geometric series, we use the following formula:
\({S_n} = \frac{{a\left( {{r^n} – 1} \right)}}{{(r – 1)}}\)
Where,
a is the first terms,
\(n\) is the number of terms.

Learn About Arithmetic Progression Here

We hope this article on Sum to n terms of Special Series has helped you. If you have any queries, drop a comment below, and we will get back to you.