Theorems on probability: The probability of the event is the chance of its occurrence. Theorems of probability tell the rules and conditions related to the addition, multiplication of two or more events. Probability density functions are statistical measures that are used to predict the likely outcome of a discrete value (e.g., the price of a stock or ETF). PDFs are typically plotted on a graph that resembles a bell curve, with the probability of the outcomes lying below the curve. A probability density function (PDF) is a continuous histogram with densities.

Basic Rules of Probability

The following probability rules are useful in understanding probability applications and performing multiple probability calculations.

Rule 1: \(P(A)+P(\) not \(A)=1\)
Rule 2: \(P\left( \emptyset \right) = 0\), where \(\emptyset\) is impossible event.
Rule 3: \(P(A)=1\), where \(A\) is sure event
Rule 4: \(0 \leq \mathrm{P}(\mathrm{E}) \leq 1\)
Rule 5: For any two events \(A, B\)
1. \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)
2. \(P(A \cup B)=P(A)+P(B)\), where \(A, B\) are mutually exclusive events.

Rule 1: The sum of two complementary events is one or we can say that, sum of probability of happening of an event and not happening of event is one.

Proof:

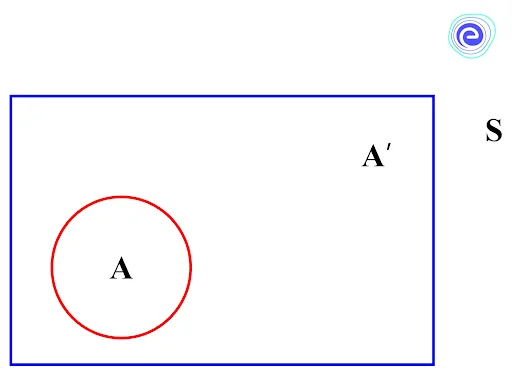
Let \(A\) be the event of a sample space \(S\)

We know that, the events \(A\) and \(A’\) will constitute the sample space.

\(\Rightarrow P(A)+P\left(A^{\prime}\right)=\frac{A}{S}+\frac{A^{\prime}}{S}\)

\(\Rightarrow P(A)+P\left(A^{\prime}\right)=\frac{A+A^{\prime}}{S}\)

\(\Rightarrow P(A)+P\left(A^{\prime}\right)=\frac{S}{S}\)

\(\Rightarrow P(A)+P\left(A^{\prime}\right)=1\)

Therefore, \(P\)(event)\(+P\)(not event)\(=1\)

Rule 2: The probability of an impossible event is zero.

Proof:

Let \(A\) be an impossible event, then \(A’\) is a sure event.

So, \(P(A)=1-P\left(A^{\prime}\right)=1-1=0\)

Rule 3: The probability of a sure event is one.

Proof:

Let \(A\) be a sure event, then the total outcomes is equals to events of sample space.

So, \(P(A)=\frac{S}{S}=1\)

Rule 4: For any event \(A\), the limits is given by \(0 \leq P(A) \leq 1\)

Proof:

Let \(A\) be any event other than impossible event.

Then the probability of the event \(A\) is \(P(A) \geq 0\).

We know that, \(A\) is the subset of sample space \(S\).

\(A \subset S\)

So, \(\mathrm{P}(\mathrm{A}) \leq 1\)

Therefore, \(0 \leq P(A) \leq 1\).

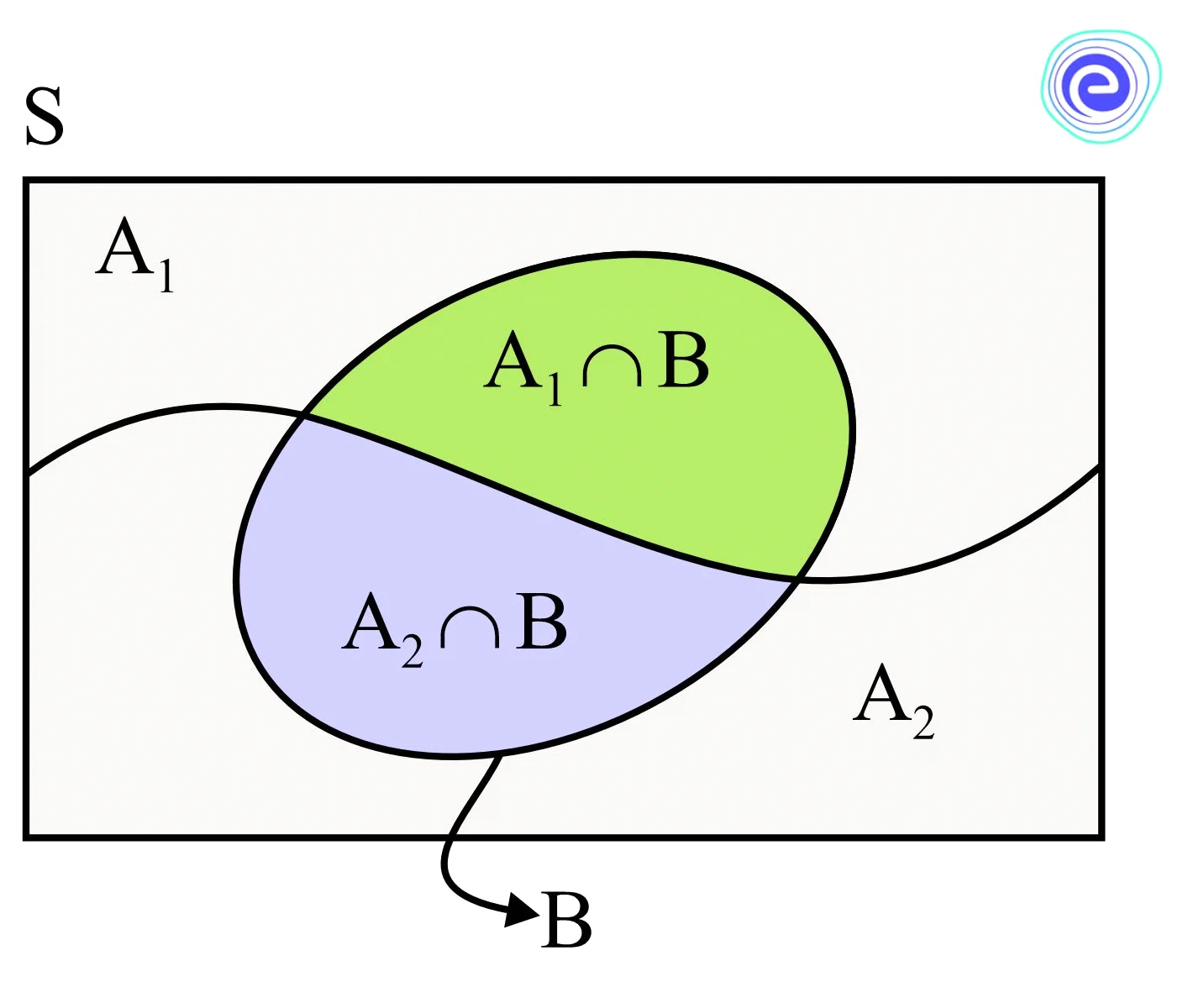
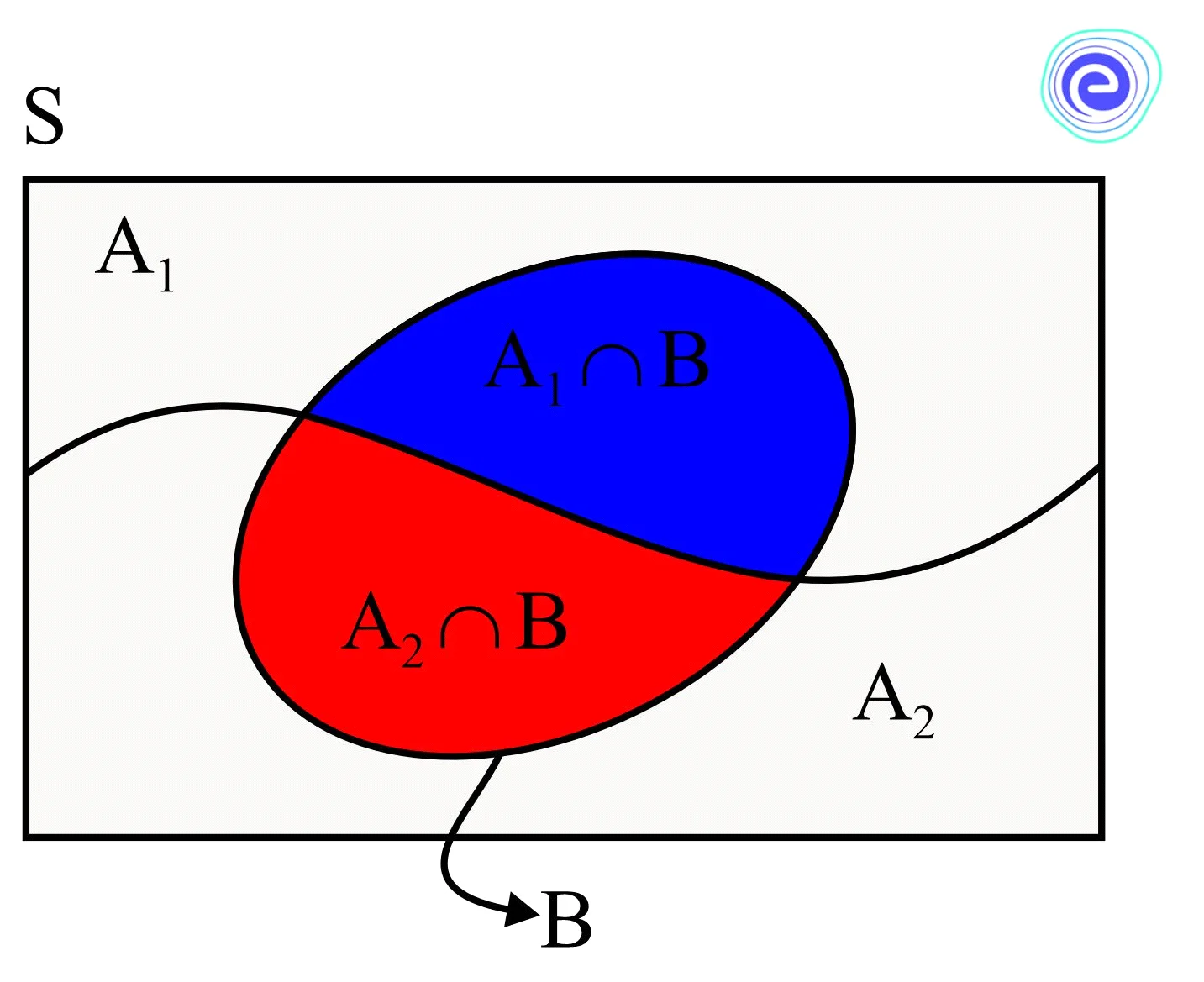
Rule 5: For two events \(A\) and \(B, P(A \cup B)=P(A)+P(B)-P(A \cap B)\)

Proof:

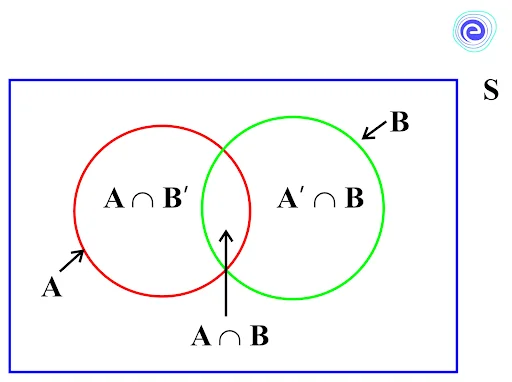
Let two events be \(A\) and \(B\)

From the Venn diagram,

\(A^{\prime} \cap B=B-(A \cap B)\) and \(A \cap B^{\prime}=A-(A \cap B)\)

Also, \(A \cup B=A \cup\left(A^{\prime} \cap B\right)\)

\(P(A \cup B)=P\left(A \cup\left(A^{\prime} \cap B\right)\right)\)

\(P(A \cup B)=P(A)+P\left(A^{\prime} \cap B\right)\)

\(P(A \cup B)=P(A)+P(B-(A \cap B))\)

\(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)

Here, \(A\) and \(B\) are two not mutually exclusive events.

If \(A\) and \(B\) are dis-joint sets or mutually exclusive events, then \(A \cap B=\varnothing\)

\(P(A \cap B)=P(\emptyset)=0\)

So,

\(P(A \cup B)=P(A)+P(B)\)

Addition Theorem of Probability

According to the addition theorem, if two events \(A\) and \(B\) are mutually exclusive, the probability of either \(A\) or \(B\) occurring is the total of the individual probabilities of \(A\) and \(B\).

For two mutually exclusive events \(A, B\)

\(P(A\) or \(B)=P(A)+P(B)\)

Proof:

Let event \(A\) happen in \(x\) ways, and event \(B\) happen in \(y\) ways.

Then the total number of happening of events is \(n\), which is \(n=x+y\)

Thus, the probability of happening events is given by \(P(A\) or \(B)\).

By the definition of probability,

\(P(A)=\frac{x}{n}\) and \(P(B)=\frac{y}{n}\)

Adding,

\(P(A)+P(B)=\frac{x}{n}+\frac{y}{n}=\frac{x+y}{n}=\frac{n}{n}=1\)

Therefore,

\(P(A\) or \(B)=P(A)+P(B)\)

Multiplication Theorem of Probability

According to the multiplication theorem of probability, the probability of both events \(A\) and \(B\) occurring is equal to the product of the probability of \(B\) occurring and the conditional probability of event \(A\) occurring if event \(B\) occurs.

Let \(A\) and \(B\) be two events associated with the sample space \(S\).

Then, \(P(A \cap B)=P(B) \cdot P\left(\frac{A}{B}\right)\)

Proof:

Let \(A\) and \(B\) be two events associated with the sample space \(S\). \(A \cap B\) gives the simultaneous occurrence of two events \(A\) and \(B\)

We know that the conditional probability of the event \(A\) given that \(B\) has occurred is given by \(P(A \mid B)\) and is given by

\(P(A \mid B)=\frac{P(A \cap B)}{P(B)}, P(B) \neq 0\)

We can write the above equation as

\(P(A \cap B)=P(A \mid B) \cdot P(B) \cdots(i)\)

Also, we can write

\(P(B \mid A)=\frac{P(B \cap A)}{P(A)}, P(A) \neq 0\)

\(P(A \cap B)=P(B \mid A) \cdot P(A)\)

Combining \((i)\) and \((ii)\), we can write

\(P(A \cap B)=P(A \mid B) \cdot P(B)=P(B \mid A) \cdot P(A)\), where \(P(B), P(A) \neq 0\)

Total Theorem of Probability

If \(A_{1}, A_{2}, A_{3}, \ldots A_{n}\) are mutually exclusive and exhaustive events in the sample space and each has non-zero probability of occurrence. Let \(B\) be any event associated with \(S\), then

\(P(B)=P\left(A_{1}\right) \cdot P\left(\frac{B}{A_{1}}\right)+P\left(A_{2}\right) \cdot P\left(\frac{B}{A_{2}}\right)+\cdots P\left(A_{n}\right) \cdot P\left(\frac{B}{A_{n}}\right)=\sum_{i=1}^{n} P\left(A_{i}\right) \cdot P\left(\frac{B}{A_{i}}\right)\)

Proof:

Given: \(A_{1}, A_{2}, A_{3}, \ldots A_{n}\) are events in the sample space \(S\).

\(A_{1} \cup A_{2} \cup A_{3} \cup \ldots A_{n}=S \text { and } A_{1} \cap A_{2} \cap A_{3} \cap \ldots A_{n}=0\)

Let \(B\) be any event in the sample space \(S\)

\(B=B \cap S\)

\(B = B \cap \left\{ {{A_1} \cup {A_2} \cup {A_3} \cup  \ldots  \ldots {A_n}} \right\}\)

\(B = \left\{ {B \cap {A_1}} \right\} \cup \left\{ {B \cap {A_2}} \right\} \ldots  \ldots  \ldots \left\{ {B \cap {A_n}} \right\}\)

\(P(B) = P\left( {\left\{ {B \cap {A_1}} \right\} \cup \left\{ {B \cap {A_2}} \right\} \ldots  \ldots  \ldots \left\{ {B \cap {A_n}} \right\}} \right)\)

\(P(B) = P\left\{ {B \cap {A_1}} \right\} \cup P\left\{ {B \cap {A_2}} \right\} \ldots  \ldots  \ldots P\left\{ {B \cap {A_n}} \right\}\)

Now, by the rule of multiplication of probability,

\(P\left(B \cap A_{i}\right)=P\left(A_{i}\right) \cdot P\left(\frac{B}{A_{i}}\right)\)

Thus, \(P(B)=P\left(A_{1}\right) \cdot P\left(\frac{B}{A_{1}}\right)+P\left(A_{2}\right) \cdot P\left(\frac{B}{A_{2}}\right)+\cdots P\left(A_{n}\right) \cdot P\left(\frac{B}{A_{n}}\right)\)

Therefore, \(P(B)=\sum_{i=1}^{n} P\left(A_{i}\right) \cdot P\left(\frac{B}{A_{i}}\right)\)

Baye’s Theorem

Let \(A_{1}, A_{2}, A_{3}, \ldots \ldots A_{n}\) be a set of events associated with a sample space \(S\), where all the events \(A_{1}, A_{2}, A_{3}, \ldots \ldots A_{n}\) have non-zero probability of occurrence. Let \(B\) be any event which occurs with \(A_{1}, A_{2}\) or \(A_{3}\) or \(\ldots \ldots A_{n}\), then according to Bayes theorem,

\(P\left(A_{i} \mid B\right)=\frac{P\left(A_{i}\right) P\left(B \mid A_{i}\right)}{\sum_{k=1}^{n} P\left(A_{k}\right) \cdot P\left(B \mid A_{k}\right)}, i=1,2,3 \ldots \ldots n\)

Proof:

Given, \(A_{1}, A_{2}, A_{3}, \ldots \ldots A_{n}\) are events in the sample space \(S\) and they are exhaustive and exclusive events.

\(A_{1} \cup A_{2} \cup A_{3} \cup \ldots \ldots A_{n}=S\) and \(A_{1} \cap A_{2} \cap A_{3} \cap \ldots \ldots A_{n}=0\)

Let \(B\) be any event in the sample space \(S\).

\(B=B \cap S\)

\(B = B \cap \left\{ {{A_1} \cup {A_2} \cup {A_3} \cup  \ldots  \ldots {A_n}} \right\}\)

\(B = \left\{ {B \cap {A_1}} \right\} \cup \left\{ {B \cap {A_2}} \right\} \ldots  \ldots  \ldots \left\{ {B \cap {A_n}} \right\}\)

\(P(B) = P\left( {\left\{ {B \cap {A_1}} \right\} \cup \left\{ {B \cap {A_2}} \right\} \ldots  \ldots  \ldots \left\{ {B \cap {A_n}} \right\}} \right)\)

\(P(B) = P\left\{ {B \cap {A_1}} \right\} \cup P\left\{ {B \cap {A_2}} \right\} \ldots  \ldots  \ldots P\left\{ {B \cap {A_n}} \right\}\)

Now, by the rule of multiplication of probability,

\(P\left(B \cap A_{i}\right)=P\left(A_{i}\right) \cdot P\left(\frac{B}{A_{i}}\right)\)

Thus, \(P(B)=P\left(A_{1}\right) \cdot P\left(\frac{B}{A_{1}}\right)+P\left(A_{2}\right) \cdot P\left(\frac{B}{A_{2}}\right)+\cdots \ldots . P\left(A_{n}\right) \cdot P\left(\frac{B}{A_{n}}\right)\)

Therefore, \(P(B) = \sum _{i = 1}^nP\left( {{A_i}} \right) \cdot P\left( {\frac{B}{{{A_i}}}} \right) \cdots (i)\)

Recalling the conditional probability, \(P\left(A_{i} \mid B\right)=\frac{P\left(A_{i} \cap B\right)}{P(B)}\cdots (ii)\)

Using the conditional probability formula of \(P\left(B \mid A_{i}\right)\)

\(P\left(A_{i} \cap B\right)=P\left(B \mid A_{i}\right) \cdot P\left(A_{i}\right) \cdots(i i i)\)

Substituting equations (i), (iii) in (ii), we get

\(P\left(A_{i} \mid B\right)=\frac{P\left(A_{i}\right) P\left(B \mid A_{i}\right)}{\sum_{k=1}^{n} P\left(A_{k}\right) \cdot P\left(B \mid A_{k}\right)}, i=1,2,3 \ldots n\)

Solved Examples on Theorems on Probability

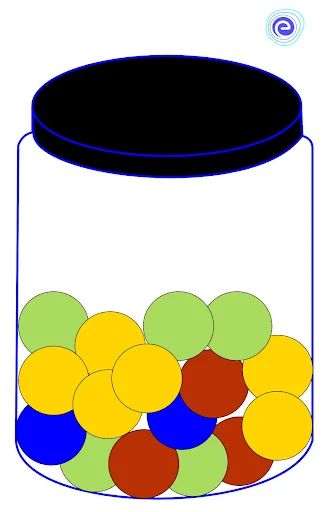
Q.1. A jar contains \(3\) red, \(2\) blue, \(5\) green and \(6\) yellow marbles. A marble is chosen at random from the jar. After replacing a first marble, a second marble is chosen. What is the probability of choosing a green and then a yellow marble?

Ans: A jar contains \(3\) red, \(2\) blue,\(5\) green, and \(6\) yellow marbles.

Total number of marbles in a jar \(=3\) red \(+2\) blue \(+5\) green \(+6\) yellow \(=16\) marbles

By, \(P({\text{event}}) = \frac{{{\text{Favourable}}\,{\text{outcomes}}}}{{{\text{Total}}\,{\text{outcomes}}}}\)

\(P(\text {Green})=\frac{5}{16}\)

\(P(\text {Yellow})=\frac{6}{16}\)

The probability of getting one green and one yellow marble is found by using the multiplication theorem, 

\(P(\text {Green and Yellow})=P(\text {Green}) \times P(\text {Yellow})\)

\(P(\text {Green and Yellow})=\frac{5}{16} \times \frac{6}{16}=\frac{30}{256}\)

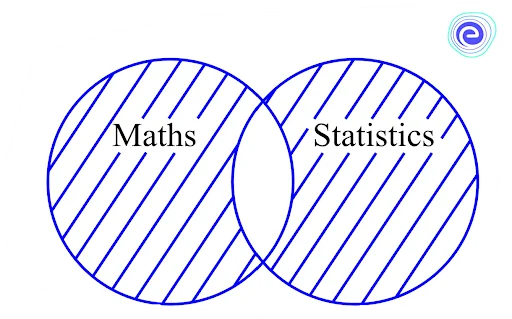
Q.2. In a class of \(125\) students, \(70\) passed in Mathematics and \(55\) passed in Statistics. Find the probability of selecting the student who passes in two subjects.

Ans: The number of students in a class is \(125\)

And, \(70\) passed in Mathematics and \(55\) passed in Statistics.

We know that, \(P({\text{event}}) = \frac{{{\text{Favourable}}\,{\text{outcomes}}}}{{{\text{Total}}\,{\text{outcomes}}}}\)

\(P\left( {{\text{Maths}} \cup {\text{Statistics}}} \right) = \frac{{125}}{{125}} = 1\)

And, \(P\left( {{\text{Maths}}} \right) = \frac{{70}}{{125}}\) and \(P\left( {{\text{Statistics}}} \right) = \frac{{55}}{{125}}\)

By, the theorem of probability,

\(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)

\(\frac{{125}}{{125}} = \frac{{70}}{{125}} + \frac{{55}}{{125}} – P\left( {{\text{Maths}} \cap {\text{Statistics}}} \right)\)

\(P\left( {{\text{Maths}} \cap {\text{Statistics}}} \right) = \frac{{30}}{{125}}\)

Q.3. Urn-\(1\) has eight red and four blue balls, whereas urn-\(2\) has five red and ten blue balls. One urn is randomly selected, and two balls are drawn from it. Calculate the chances of both balls being red.

Ans:

Given, urn-\(1\) has \(8\) red and \(4\) blue balls, whereas urn-\(2\) has \(5\) red and \(10\) blue balls.

Let \(A_{1}\) be the event of selecting urn-\(1\) and \(A_{2}\) be the event of selecting urn-\(2\).

Let \(B\) be the event of selecting \(2\) red balls.

The probability of getting two red balls is found using the total probability theorem.

\(P(B)=P\left(A_{1}\right) \cdot P\left(\frac{B}{A_{1}}\right)+P\left(A_{2}\right) \cdot P\left(\frac{B}{A_{2}}\right)\)

\(P(B)=\frac{1}{2} \times \frac{8 C_{2}}{12 C_{2}}+\frac{1}{2} \times \frac{5 C_{2}}{15 C_{2}}\)

\(P(B)=\frac{1}{2} \times \frac{14}{33}+\frac{1}{2} \times \frac{2}{21}\)

\(P(B)=\frac{20}{77}\)

Hence, the probability of getting two red balls is \(\frac{20}{77}\).

Q.4. Suppose the probability of an event \(A\) is \(0.1\). Find the probability of not getting the event \(A\).

Ans: Given: The probability of \(A\) is \(0.1\).

Probability of not getting an event \([P(\operatorname{not} A)]\) and probability of getting event \(\mathrm{A}\) are complementary events.

So, by the theorem of probability,

\(P(A)+P(\operatorname{not} A)=1\)

\(P(\operatorname{not} A)=1-P(A)=1-0.1=0.9\)

Hence, the probability of not getting event \(A\) is \(0.9\)

Q.5. There are two machines in a factory: I and II. Machine-I produces \(40\%\) of the production, whereas Machine-II produces \(60\%\) of the output. In addition, \(4\%\) of goods produced by Machine-I and \(5\%\) of things produced by Machine-II are defective. Find the chance that an item is defective if it is drawn at random.

Ans: Given, machine I produces \(40 \%\) of the production and \(4 \%\) are defective. Machine II produces \(60 \%\) of the production and \(5 \%\) are defective.

Let \(A_{1}\) be the event of selecting machine \(I\) and \(A_{2}\) be the event of selecting machine II.

Let \(B\) be the event of selecting a defective item.

The probability of getting a defective item is found using the total probability theorem.

\(P(B)=P\left(A_{1}\right) \cdot P\left(\frac{B}{A_{1}}\right)+P\left(A_{2}\right) \cdot P\left(\frac{B}{A_{2}}\right)\)

\(P(B)=0.4 \times 0.04+0.6 \times 0.05\)

\(P(B)=0.046\)

Hence, the probability of getting a defective item is \(0.046\)

Summary

Probability is the chance of getting things to happen. There are various terms associated with probability, such as random experiment, sample space, event, outcome, impossible and sure events. There are five theorems in a probability, such as the probability of impossible and sure events is \(0\) and \(1\). The sum of probabilities of complementary events is one.

The addition theorem of probability states that it is the sum of probabilities of two mutually exclusive events and the multiplication theorem of probability is the product of independent events.

Frequently Asked Questions (FAQs)

Q.3. What is the addition theorem of probability?
Ans: According to the addition theorem, if two events \(A\) and \(B\) are mutually exclusive, the probability of either \(A\) or \(B\) occurring is the total of the individual probabilities of \(A\) and \(B\)

Q.4. What is the concept of probability?
Ans: Probability is the mathematical concept of studying uncertain things. It is the ratio of favourable outcomes to the total number of outcomes.

Q.5. What is the multiplication theorem of probability?
Ans: According to the multiplication theorem, the probability that two independent events \(A\) and \(B\) will occur is equal to the product of their probabilities.

ATTEMPT MATHS MOCK TESTS

We hope this detailed article on Theorems on Probability is helpful to you. If you have any queries on this article or in general about Theorems on Probability, ping us through the comment box below and we will get back to you as soon as possible.