Towards Quantum Mechanical Model of the Atom: Bohr is widely credited with developing the first quantitatively successful model of the atom. However, the newer Wave Mechanical Theory has entirely replaced it. The new idea contradicts Bohr’s visualisation of electrons moving in tight orbits. The Wave Mechanical Theory made a significant breakthrough by proposing that electron motion is complicated and best represented by wave characteristics and probability.

Discoveries Leading Towards Quantum Mechanical Model

de Broglie Equation

We have studied that light shows dual nature, i.e., Wave nature (Electromagnetic Radiation) and Particle nature (photons).
After quantum theory, de Broglie proposed that, like light, an electron behaves both as a particle and a wave. So, a new approach was proposed, which is called Wave Mechanical Model of Matter or Dual Nature of Matter.

According to him, every form of matter (electron or proton or any other particle) behaves like a wave in some circumstances. These were called Matter-waves or de Broglie waves. de Broglie derived an expression for calculating the $\lambda$ of the wave associated with the electron.

According to Planck’s theory: $\mathrm{E}=\mathrm{h}\mathrm{v}=\mathrm{h}\frac{\mathrm{c}}{\lambda }$
According to Einstein theory: $\mathrm{E}=\mathrm{m}{\mathrm{c}}^2$
With the help of both the above equations we get
$\lambda =\frac{\mathrm{h}}{\mathrm{p}}=\frac{\mathrm{h}}{\mathrm{m}\mathrm{v}}$
$\mathrm{m}=$ Mass of the particle
$\mathrm{v}=$ Velocity of the particle
$\mathrm{p}=$ Momentum of the particle

Heisenberg’s Uncertainty Principle

Due to the wave nature of electrons in an atom, it is now highly impossible to ascertain the exact whereabouts of an electron. Heisenberg’s Uncertainty Principle defines this idea as:

“It is impossible to specify both the momentum and the position of a subatomic particle like an electron at any given instant.”

Whenever there is an attempt to specify the electron’s position precisely, uncertainty is introduced in its momentum and vice-versa. If $\mathrm{\Delta }\mathrm{x}$ is the uncertainty in position and $\mathrm{\Delta }\mathrm{p}$ is the uncertainty in its momentum, then according to Heisenberg, these quantities are related as follows:
$\mathrm{\Delta }\mathrm{x}\cdot \mathrm{\Delta }\mathrm{p}\ge \frac{\mathrm{h}}{4\pi }$

Hence, in new atomic theory, an electron cannot be regarded as having fixed (definite) paths around the nucleus, called orbits. It is a matter of probability that an electron is more likely to be found in one place or the other. So, we can now visualise a region in space (diffused cloud) surrounding the nucleus, where the probability of finding the electron is maximum. Such a region is called an Orbital. It can be defined as, “the electron distribution described by a wave function and associated with a particular energy.”

Quantum Mechanical Model of Atom

Fundamental Equation of Quantum Mechanics

The motion of all macroscopic objects is successfully described by classical mechanics based on Newton’s equations of motion. Classical mechanics, on the other hand, fails when applied to microscopic particles such as electrons and atoms because it overlooks the concept of the dual behaviour of matter and the uncertainty principle.

Quantum Mechanics is the branch of science that deals with this dual behaviour of matter. It has to do with the study of the motions of microscopic objects that have both wave-like and particle-like features that can be observed.

Quantum Mechanics was developed in $1926$ by Werner Heisenberg and Erwin Schrodinger. Schrodinger develops the fundamental equation of Quantum Mechanics. It is

$\frac{{\partial }^2\psi }{\partial {\mathrm{x}}^2}+\frac{{\partial }^2\psi }{\partial {\mathrm{y}}^2}+\frac{{\partial }^2\psi }{\partial {\mathrm{z}}^2}+\frac{8{\pi }^2\mathrm{m}}{{\mathrm{h}}^2}(\mathrm{E}–\mathrm{V})\psi =0$

or $\hat{\mathrm{H}}\psi =\mathrm{E}\psi$ where $\hat{\mathrm{H}}$ is a mathematical operator called Hamiltonian.
$\psi$ is the amplitude of the wave
$\mathrm{x},\mathrm{y},\mathrm{z}$ are coordinates of the position of electron
$\mathrm{E}$ is total energy of electron
$\mathrm{V}$ is potential energy
$\mathrm{m}$ is the mass of electron
$\mathrm{h}$ is Planck’s constant

The importance of the wave equation solution is that it provides a set of numbers called Quantum Numbers.

Quantum Numbers

A set of four numbers is used to describe the electrons around the nucleus in an atom, called Quantum Numbers. These are designed in such a way that the states available to electrons satisfy quantum or wave mechanics laws.

There are four quantum numbers which are given as follows:
1. Principal Quantum Number
2. Azimuthal Quantum Number
3. Magnetic Quantum Number
4. Spin Quantum Number

Principal Quantum Number

The principal quantum number is denoted by $\mathrm{n}$. It was given by Bohr. This number represents the main energy levels (principal energy levels) designated as $\mathrm{n}=1,2,3\dots$ or the corresponding shells are named as $\mathrm{K},\mathrm{L},\mathrm{M},$ and $\mathrm{N}$ respectively.

(a) Higher is the value of $\mathrm{n}$, greater is its distance from the nucleus, greater is its size, and greater is its energy.
(b) It also gives the total electrons that may be accommodated in each shell; the capacity of each shell is given by the formula $2{\mathrm{n}}^2$, where n is the principal quantum number.
(c) The principal quantum numbers can be used to determine angular momentum.

Azimuthal Quantum Number

The azimuthal quantum number is denoted by $\mathrm{l}$. It was given by Somerfield. This number represents the energy associated with the electron’s angular momentum around the nucleus.

(a) It can assume all integral values from $0$ to $\mathrm{n}–1$. The possible values of $\ell$ are $1,2,3\dots \dots ,\mathrm{n}–1$.
(b) Each value of $\ell$ describes a particular sub-shell within the main energy level and determines the shape of the electron cloud.
(c) The orbital angular momentum of the electron $=\sqrt{\ell (\ell +1)}\frac{\mathrm{h}}{2\pi }$.

Magnetic Quantum Number

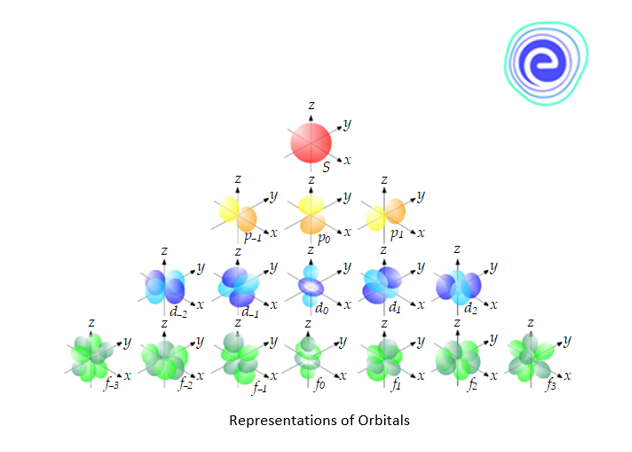
The magnetic quantum number is denoted by $\mathrm{m}$. It was given by Linde to explain the Zeeman Effect. An electron has an angular momentum; its motion may be likened to the flow of an electric current through a loop. Such a flow of current creates a magnetic field. This field can interact with an external magnetic or electric field; as a result of this interaction, the electron in a given energy sublevel orient themselves in certain specific regions of space around the nucleus. These regions of space are called Orbitals.

The magnetic quantum number determines the induced magnetism. The number of possible sub-energy level orientations is defined by the values of $\mathrm{m}$.

(a) $\mathrm{m}$ can have any integral values between $–\ell$ to $+\ell$ including $0$ i.e.., $\mathrm{m}=–\ell ,-\ell +1,\dots \dots \dots ,0,1,2,3,\dots \dots \dots ,\ell –1,+\ell$. We can say that a total of $(2\ell +1)$ values of $\mathrm{m}$ are there for a given value of $\mathrm{l}$.
(b) In $\mathrm{s}$ subshell, there is only one orbital $\ell =0,\Rightarrow \mathrm{m}=(2\ell +1)$
(c) In the $\mathrm{p}$ subshell, there are three orbitals corresponding to three values of $\mathrm{m}:–1,0$ and $1$. $\ell =1\Rightarrow \mathrm{m}=(2\ell +1)=3$. These three orbitals are represented as ${\mathrm{p}}_{\mathrm{x}},{\mathrm{p}}_{\mathrm{y}},{\mathrm{p}}_{\mathrm{z}}$ along $\mathrm{x},\mathrm{y},\mathrm{z}$ axes perpendicular to each other.
(d) In the $\mathrm{d}$ subshell, there are five orbitals corresponding to $–2,–1,0,+1$ and $+2$.
(e) $\ell =2\Rightarrow \mathrm{m}=(2\ell +1)=5$. These five orbitals are represented as ${\text{d}}_{\text{xy}}\text{,}{\text{d}}_{\text{yz}}\text{,}{\text{d}}_{\text{zx}}\text{,}{\text{d}}_{{\text{x}}^{\text{2}}\text{ – }{\text{y}}^{\text{2}}}\text{,}{\text{d}}_{{\text{z}}^{\text{2}}}$
(f) In $\mathrm{f}$ subshell there are seven orbitals corresponding to $–3,-2,-1,0,+1,+2,+3,\ell =3\Rightarrow \mathrm{m}=(2\ell +1)=7$.

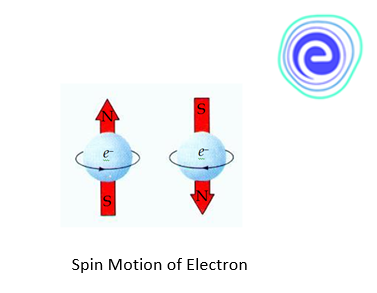
Spin Quantum Number

The electron behaves as if it were rotating around a centre. The two possible values for the spin quantum number correspond to the two directions of spin.

When an electron rotates around a nucleus, it also spins about its axis. If the spin is clockwise, its spin quantum number is $+1/2$ and represented as $\uparrow$ . If the spin is anti-clockwise, its value is $–1/2$ and is represented as $\downarrow$ . If the value of $\mathrm{s}$ is $+1/2$, then by convention, we take that electron as the first electron in that orbital, and if the value of $\mathrm{s}$ is $–1/2$, it is taken as the second electron.

Summary of Towards Quantum Mechanical Model of the Atom

• Following quantum theory, de Broglie postulated that an electron, like light, operates as both a particle and a wave.
• According to Heisenberg’s uncertainty principle, “It is impossible to specify both the momentum and the position of a subatomic particle like an electron at any given instant.”
• Quantum Mechanics was developed in $1926$ by Werner Heisenberg and Erwin Schrodinger. Schrodinger develops the fundamental equation of Quantum Mechanics.
• The importance of the wave equation solution is that it provides a set of numbers called Quantum Numbers.
• There are four quantum numbers which are given as follows:
  Principal quantum number, Azimuthal quantum number, Magnetic quantum number and Spin quantum number.

FAQs on Towards Quantum Mechanical Model of the Atom

Q.1. What are de Broglie waves?
Ans: After quantum theory, de Broglie proposed that, like light, an electron behaves both as a particle and a wave. So, a new approach was proposed, which is called Wave Mechanical Model of Matter or Dual Nature of Matter. According to him, every form of matter (electron or proton or any other particle) behaves like a wave in some circumstances. These were called Matter-waves or de Broglie waves.

Q.2. What is Heisenberg’s uncertainty principle?
Ans: Due to the wave nature of electrons in an atom, it is now highly impossible to ascertain the exact whereabouts of an electron. Heisenberg’s Uncertainty Principle defines this idea as: “It is impossible to specify both the momentum and the position of a subatomic particle like an electron at any given instant.”

Q.3. What is an orbital?
Ans: In new atomic theory, an electron cannot be regarded as having fixed (definite) paths around the nucleus, called orbits. It is a matter of probability that an electron is more likely to be found in one place or the other. So, we can now visualize a region in space (diffused cloud) surrounding the nucleus, where the probability of finding the electron is maximum. Such a region is called an Orbital.

Q.4. What is represented by the principal quantum number?
Ans: The principal quantum number is denoted by $\mathrm{n}$. It was given by Bohr. This number represents the main energy levels (principal energy levels) designated as $\mathrm{n}=1,2,3\dots$ or the corresponding shells are named as $\mathrm{K},\mathrm{L},\mathrm{M},$ and $\mathrm{N}\dots ..$ respectively.

Q.5. How many orbitals are present in f subshell?
Ans: Seven

Know About Wave Nature of Matter Here

We hope this article on Towards Quantum Mechanical Model of the Atom has helped you. If you have any queries, drop a comment below, and we will get back to you.