স্বয়ংক্ৰিয়ভাৱে প্ৰশ্নোত্তৰ সমাধানকাৰী প্ৰযুক্তি
এডটেক প্লেটফৰ্ম হিচাপে ছাত্ৰ-ছাত্ৰীসকলক শ শ পৰীক্ষাৰ পাঠ্যক্ৰমৰ পৰা হাজাৰ হাজাৰ ধাৰণা সম্পৰ্কে প্ৰশ্ন অনুশীলন কৰিবলৈ অনুমতি দিয়ে, Embibeয়ে ছাত্ৰ-ছাত্ৰীসকলক এটা বিশেষ প্ৰশ্ন কেনেকৈ সমাধান কৰিব পাৰি সেইটো বুজিবলৈ সহায় কৰিবলৈ ব্যাখ্যা আৰু পদক্ষেপ-দ্বাৰা-পৰ্যায়ৰ সমাধান গাইডৰ সৈতে প্ৰশ্নসমূহ সমৃদ্ধ কৰাত বিনিয়োগ কৰিছে। এইটো এটা মেনুৱেল প্ৰক্ৰিয়া হৈ আহিছে য’ত মানৱ বিষয় বিশেষজ্ঞসকলে প্ৰশ্নসমূহ সমাধান কৰে।
এম্বাইবৰ প্ৰশ্ন তথ্য গোট বৃদ্ধি হৈ অহাৰ লগে লগে, মেনুৱেলি সৃষ্টি কৰা সমিধানসমূহৰ ওপৰত নিৰ্ভৰ কৰাটো নিষেধমূলকভাৱে ব্যয়বহুল হৈ পৰিল। সমাধানকাৰী প্ৰযুক্তি এতিয়াও এক তুলনামূলকভাৱে বৰ্ধনশীল ক্ষেত্ৰ যি মধ্যৱৰ্তী স্তৰৰ গণিতৰ দৰে কিছুমান নিৰ্দিষ্ট ক্ষেত্ৰত পাঠ প্ৰশ্ন সমাধান কৰাৰ বাবে সূত্ৰ সৃষ্টি কৰাত কিছু সফলতা লাভ কৰিছে।
বহু সংখ্যক প্ৰশ্নৰ উত্তৰ আৰু পদক্ষেপ অনুসৰি সমাধান স্বয়ংক্ৰিয়ভাৱে সৃষ্টি কৰিবলৈ সক্ষম হ’বলৈ Embibe য়ে এই ক্ষেত্ৰত গৱেষণা কৰি আছে।
সমস্যাৰ বিৱৰণ
গণিতৰ প্ৰশ্নৰ বাবে, সমাধানকাৰী কোড ব্যৱহাৰ কৰি সমাধান কৰা আৰু এটা ষ্টেপ-বাই-ষ্টেপ সমাধান কৰা।
প্ৰশ্নটো শিক্ষাৰ্থীৰ পৰা অহা কোনো মুকলি প্ৰশ্ন হ’ব পাৰে আৰু কোনো নিৰ্দিষ্ট সজ্জাত থকাটো প্ৰয়োজনীয় নহয়। আমি এয়া সমাধান কৰিবলৈ আৰু সমিধানৰ খোজবোৰ প্ৰদান কৰিবলৈ চেষ্টা কৰিম।
পদ্ধতি
সমগ্ৰ প্ৰক্ৰিয়াটো দেখাত এই ধৰণৰ:
উদাহৰণস্বৰূপে,
এয়া হৈছে অসম বোৰ্ডৰ ষষ্ঠ শ্ৰেণীৰ এটা প্ৰশ্ন:
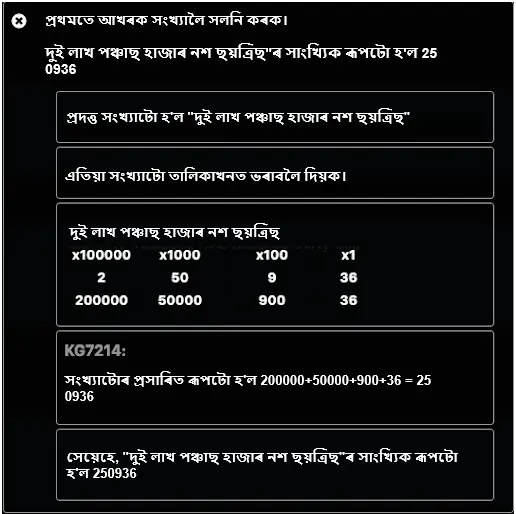
“সংখ্যাত লিখা – দুই লাখ পঞ্চাশ হাজাৰ ন শ ছয়ত্ৰিশ।”
সেয়ে, প্ৰথম স্তৰত, আমি সেই সমাধানকাৰী কোড পূৰ্বানুমান কৰিবলৈ চেষ্টা কৰিম যি ব্যৱহাৰ কৰি এই প্ৰশ্নৰ সমাধান কৰিব পৰা যাব, যি হৈছে “পাঠ_পৰিৱৰ্তন_কৰা_সংখ্যালৈ”।
পৰৱৰ্তী পৰ্যায়ত আমি ইয়াক মূল্যায়ন কৰিবলৈ পূৰ্বানুমান কৰা সমাধানকাৰীৰ বাবে যুক্তিটো আনিম। গতিকে, এই ক্ষেত্ৰত সমাধানকাৰীলৈ ইনপুট যুক্তি হ’ব “দুই লাখ পঞ্চাশ হাজাৰ ন শ ছয়ত্ৰিশ”।
সেয়ে, আমি সম্পূৰ্ণ সমাধানকাৰী পাওঁ
পাঠ_পৰিৱৰ্তন_কৰা_সংখ্যালৈ(দুই লাখ পঞ্চাশ হাজাৰ ন শ ছয়ত্ৰিশ)।
তাৰ পিছত আমি উত্তৰ আৰু ষ্টেপ-বাই-ষ্টেপ সমাধান পাবলৈ যুক্তিটোৰে সমাধানকাৰীক মূল্যায়ন কৰোঁ, তেতিয়া এনে দেখা যায়:
আহা আমি আন এক প্ৰশ্নৰ উদাহৰণৰ সৈতে বিস্তাৰ কৰোঁ:
“শ্ৰীমতী চোনীয়ে 7 1/2 লিটাৰ গাখীৰ কিনে।যদি তাৰ পৰা তেওঁ 5 3/4 লিটাৰ গাখীৰ খায়। তেওঁৰ ওচৰত কিমান গাখীৰ বাকী থাকিল?”
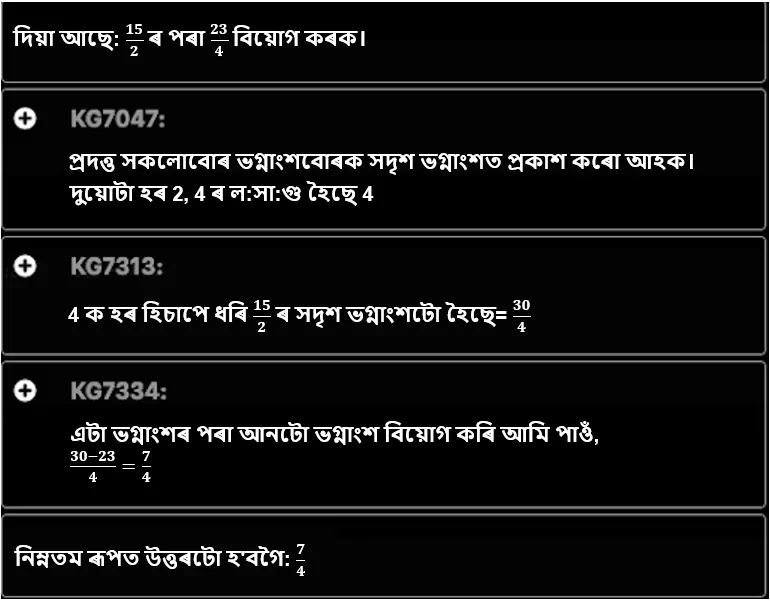
এয়া “বিয়োগ_ভগ্নাংশ_মিশ্ৰিত_প্ৰকাৰ(7 1/2, 5 3/4)” সমাধানকাৰী সূত্ৰ ব্যৱহাৰ কৰি সমাধান কৰিব পৰা যায়।
আমি সমিধানবোৰ পৰ্যায়গত ৰূপত এইদৰে পাম।
সমাধান
আমি সমাধানটো দুটা ভাগত ভাগ কৰিব পাৰোঁ।
- সমাধানকাৰী ক’ড পূৰ্বানুমান
- যুক্তি আহৰণৰ জৰিয়তে
সমাধানকাৰী ক’ড পূৰ্বানুমানত আমি কোনবোৰ গণিতৰ সমস্যা সমাধান কৰিব পাৰি সেইটো ব্যৱহাৰ কৰি সমাধানকাৰী ক’ডবোৰ পূৰ্বানুমান কৰিবলৈ চেষ্টা কৰোঁ। উদাহৰণস্বৰূপে, ওপৰৰ উদাহৰণটোত, “বিয়োগ_ভগ্নাংশ_মিশ্ৰিত_প্ৰকাৰ” আছিল সঠিক সমাধানকাৰী যাক ব্যৱহাৰ কৰি প্ৰদত্ত সমস্যাটো সমাধান কৰিব পাৰি। আমি T5[1] ৰ দৰে ডিপ লাৰ্নিং জেনেৰেটিভ seq2seq মডেল ব্যৱহাৰ কৰিব পাৰো, যিয়ে সমাধানকাৰী ক’ড সৃষ্টি কৰিব পাৰে যিয়ে সমস্যাটো সমাধান কৰিব।
আমি দ্বিতীয় পদক্ষেপলৈ আগবঢ়াৰ আগতে, আমাক প্ৰতিটো সমাধানকাৰী সূত্ৰৰ বাবে 1টা নমুনা সমাধানকাৰী লাগিব যুক্তিৰ সৈতে। উদাহৰণস্বৰূপে, “বিয়োগ_ভগ্নাংশ_মিশ্ৰিত_প্ৰকাৰ” বাবে এক নমুনা সমাধানকাৰী হ’ব পাৰে “subtract_fractions_mixed_type(1 2/3, 4 5/6)” ধৰণৰ হ’ব পাৰে। এয়া কিদৰে উপকাৰী হ’ব, আমি শীঘ্ৰে অম্বেষণ কৰিম।
এবাৰ আমি প্ৰদত্ত সমস্যাটো সমাধান কৰিব পৰা পূৰ্বানুমান কৰা সমাধানকাৰী ক’ডটো পালেই আমি প্ৰশ্নটোৰ পৰা যুক্তিবোৰ আনিব লাগিব। তাৰ বাবেও আমি T5[1] ৰ দৰে জেনেৰেটিভ seq2seq মডেল ব্যৱহাৰ কৰিব পাৰো। জ্ঞানৰ গ্ৰাফসমূহত ধৰা পৰা অৰ্থগত সম্পৰ্কসমূহৰ লাভ উঠাবলৈ এনে ভাষাৰ আৰ্হিসমূহক জ্ঞান ইনপুটৰ সৈতে আৰু অধিক সম্প্ৰসাৰিত কৰা হয় [3][4] । আমি পূৰ্বানুমান কৰা সমাধানকাৰীৰ বাবে সমস্যাৰ বিৱৰণ আৰু নমুনা সমাধানকাৰী দিব পাৰো। আৰু আমি T5[1] মডেলৰ পৰা প্ৰশ্নবোৰৰ পৰা প্ৰকৃত যুক্তিৰ সৈতে সমাধানকাৰী ক’ডটো পাম। গতিকে শেষত আমাৰ ওচৰত ওপৰৰ উদাহৰণটোৰ পৰা যুক্তি অৰ্থাৎ “subtract_fractions_mixed_type(7 1/2, 5 3/4)” থকা সমাধানকাৰী ক’ডটো থাকিব।
আমি লগতে তুলনামূলকভাৱে সৰল পদ্ধতি কিছুমান ব্যৱহাৰ কৰিব পাৰোঁ প্ৰশ্নটোৰ পৰা যুক্তি সমূহ লোৱাৰ বাবে। যেনে, যদি আমাৰ ওচৰত প্ৰতিটো সমাধানকাৰীৰ বাবে তথ্যৰ প্ৰকাৰ আৰু যুক্তিবোৰৰ নমুনা থাকে, যি আমাৰ ক্ষেত্ৰত আছে, আমি প্ৰশ্নটোৰ পৰা সদৃশ সংখ্যাবোৰ ল’বলৈ চেষ্টা কৰিব পাৰোঁ।
এইদৰে আমি সমাধানকাৰী সূত্ৰ পূৰ্বানুমান কৰিম আৰু প্ৰশ্নটোৰ পৰা সমাধানকাৰী যুক্তি বোৰ ল’ম। এবাৰ আমি এই দুয়োটা পালে, আমি কেৱল সমাধানকাৰী ত গণনা কৰিব লাগিব শুদ্ধ উত্তৰ আৰু ঢাপ-অনুযায়ী সমিধান পাবলৈ।
তথ্যসূত্ৰ
[1] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, Peter J. Liu. “Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer”
[2] Amini, Aida, Saadia Gabriel, Peter Lin, Rik Koncel-Kedziorski, Yejin Choi, and Hannaneh Hajishirzi. “MathQA: Towards interpretable math word problem solving with operation-based formalisms.” arXiv preprint arXiv:1905.13319 (2019