At Embibe, we help students improve their scores in standardized examinations by incorporating insights and models from learning theory and education research through item response theory models.
One widely used model named Item Response Theory[1, 2] predicts a student’s likelihood of answering a question correctly by estimating the student’s skill or ability level and the difficulty level of the question being attempted. It was first proposed in the 1960s, and many variants of this exist today, such as the 1PL model[2, 3] and the 2PL model[2].
1PL Model of Item Response Theory
The 1PL or 1 parameter Item Response Theory model, also known as the Rasch model[3] is described as follows.
Let i be a learner or student; j be a question. Let θi be the learner’s ability and βj the question’s difficulty level. Then as per the 1PL model, the probability Pij of the ith user correctly answering the jth question is given as Pij = 1 / (1 + exp(θi – βj)) The term βj – θi represents the difference between the difficulty of the question (βj) and the ability of the learner (θi). The probability of a correct response is modelled using the logistic function, which maps the difference to a probability value between 0 and 1.
The logit function, which is the inverse of the logistic function, is used to transform the probability back to a log-odds scale. The logit function is defined as follows:
- logit(x) = log(x / (1 – x))
Using the 1PL Item Response Theory parameter estimation techniques, we can predict the ability level θi of a learner, given the data about the learner’s response to each attempted question.
A Deep Learning Architecture for 1PL Item Response Theory
The 1PL item response theory model is indeed logistic regression with a domain-specific parametrization. Consequently, we can realize such a model using any deep learning framework. The deep learning architecture for the 1PL model is shown in Figure 1.
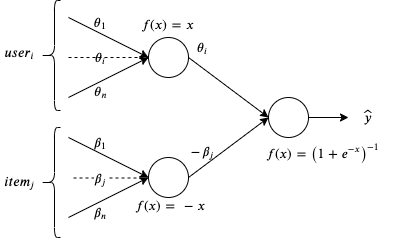
Figure 1: Neural Network Architecture for Estimating the 1PL IRT Model Parameters
Our model is implemented in Keras[4] as a deep neural network. The advantages of modelling the problem as a neural network are:
- Ability to handle missing values in the input — not every user needs to attempt every question,
- Ability to scale to a large number of users and items,
- Ability to extend the framework to 2PL, 3PL and other Item Response Theory models with more parameters.
We refer to this model as the 1PL Deep Item Response Theory model.
Validation
In order to benchmark and validate the modelling strategy, we generate simulated data as follows:
- i N(0,1): learner ability is generated using a normal distribution with mean 0 and standard deviation 1,
- j U(-1,1): question difficulty values are uniformly generated between -1 and 1,
- Pij= i – j: the probability of correct responses is calculated using user ability and item difficulty (using the 1PL Item Response Theory equation),
- yijk Bern(Pij): binary responses (correct, not-correct) are sampled from the Bernoulli distribution with success probability Pij, where the number of responses per item per learner is configurable.
We have simulated 100 questions, 100 learners, and one response per learner per question using applications of item response theory to practical testing problems.
We fit the 1PL Deep Item Response Theory model to the simulated dataset. Inputs to the neural network are the user vector (one-hot encoded) and the question vector (also one-hot encoded), and outputs are the parameters of the Item Response Theory model, including item difficulty, learner ability and prediction of whether the learner will answer correctly or not. The neural network is fully connected. It has two input layers, intermediate layers for difficulty and ability, and one output layer for prediction.
We compare the 1PL Deep Item Response Theory output from the neural network with the true outputs from the simulated data.
Implementation
Model: The architecture of 1PL Item Response Theory is defined by harnessing the compositionality of NNs, utilizing Keras functional APIs. The overall model is structured by stacking Dense layers – here, 2 Dense layers for the 1PL model, each representative of a User or Item parameters pivotal in driving the likelihood (Pij) of a user (i) responding to an Item (j).
Hyper Parameters: The following default settings are used in each dense layer
- Kernel & Bias initializers: Normal (0,1)
- l1/l2 regularizations: l_1=0, l_2=0
- Activity regularizers: l_1=0, l_2=0
A developer can override the above settings, or the best configuration can be obtained by searching over a space of configurations for item response theory parameter estimation techniques. Such details will be in a forthcoming blog. The defined model is flexible enough to extend its usage for two or even three parameters, namely discrimination and guessability, and consequently, in retrospect, an extended model coupled with Neural Architecture Search capability can be constrained to perform as one or two PL models.
Experimental Results
The below plots show the correlation between:
- Predicted difficulty versus true difficulty level, with Pearson correlation coefficient 0.9857.
- Predicted ability versus true ability level, with Pearson correlation coefficient 0.9954.
- Predicted probability of answering each question correctly versus true probability, with Pearson correlation coefficient 0.9926.
From the Deep Item Response Theory model trained on 1PL data, the log-likelihood of the 1PL DIRT model is 0.587.
As we can see, we get a good correlation in all three cases, indicating that our 1PL Deep Item Response Theory model successfully predicts the difficulty, ability and test score with good accuracy.

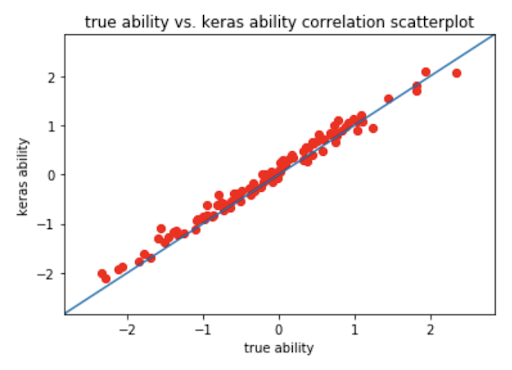
Figure 2: Scatterplots of the True Versus Derived Keras Model Difficulty and Ability Parameters

Figure 3: Hexbin Plot of the True Probability of Answering the Questions Correctly Versus. The Probability Derived from our Trained Keras Model
Conclusion
We have shown that, based on simulations, the 1PL Item Response Theory model can be implemented via a Deep Learning model. Using the Item Response Theory parameters, we can get good estimates of learner ability and the difficulty level of the questions using our 1PL Item Response Theory-based model. These estimates can, in turn, be used in generating adaptive tests, goal setting, and other downstream problems.
References
- Frank B. Baker. “The basics of item response theory.” ERIC, USA, 2001
- Wikipedia. Item Response Theory https://en.wikipedia.org/wiki/Item_response_theory
- Georg Rasch. “Studies in mathematical psychology: I. Probabilistic models for some intelligence and attainment tests.” 1960.
- Keras Deep Learning framework: Keras