स्फेरोमीटर या गोलाईमापी प्रयोग

गोलीय पृष्ठ की वक्रता त्रिज्या क्या है?

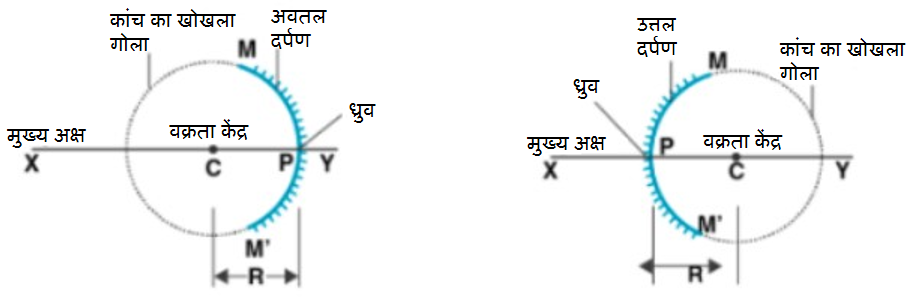
गोलीय पृष्ठ, गोले का वह भाग होता है, जिसका उपयोग प्रकाश के परावर्तन के सिद्धांत का उपयोग करके किसी वस्तु का अभीष्ट प्रतिबिंब बनाने के लिए किया जाता है। गोलीय पृष्ठ दो प्रकार के होते हैं: उत्तल और अवतल।

ध्रुव और वक्रता केंद्र के बीच की रेखीय दूरी को वक्रता त्रिज्या कहा जाता है। गोलीय पृष्ठ के केंद्र को ध्रुव कहा जाता है, जबकि गोले के केंद्र (जिससे गोलीय पृष्ठ को काटा जाता है) को वक्रता केंद्र कहा जाता है। जब वक्रता त्रिज्या अनंत हो जाती है, तो गोलीय दर्पण एक समतल दर्पण के रूप में व्यवहार करता है। वक्रता त्रिज्या गोलीय पृष्ठ के मुख्य अक्ष पर स्थित होती है।

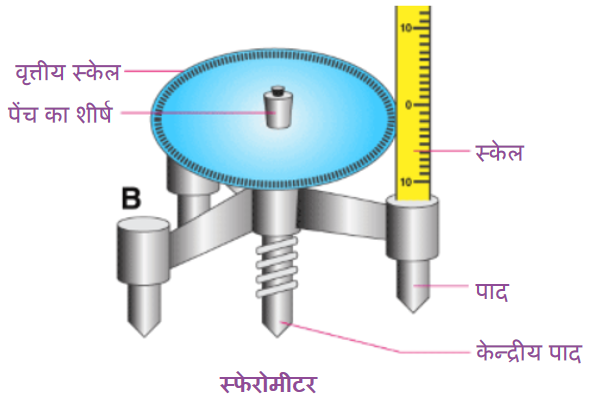
स्फेरोमीटर का चित्र

नीचे एक स्फेरोमीटर का नामांकित आरेख दिया गया है।

स्फेरोमीटर से पाठ्यांक कैसे लिया जाता है?

स्फेरोमीटर का उपयोग करने के लिए निम्नलिखित प्रक्रिया अपनाई जाती है:

• पहले, उपकरण को पूर्णतः समतल पृष्ठ पर रखिए, ताकि केंद्रीय पाद को तब तक धीरे-धीरे नीचे किया जा सके, जब तक कि यह सतह को स्पर्श नहीं कर ले। जब केंद्रीय पाद पृष्ठ को स्पर्श करता है, तो उपकरण केंद्रीय पाद के परितः चक्कर लगाता है।
• माइक्रोमीटर पेंच से पाठ्यांक लेने के लिए सतह से स्फेरोमीटर को हटा दें। यदि उपकरण ठीक से कार्य करता है, तो पाठ्यांक 0-0 होना चाहिए। हालांकि, उपकरण में हमेशा एक अल्प त्रुटि होती है, जो या तो धनात्मक या ऋणात्मक त्रुटि हो सकती है।
• उपकरण को पृष्ठ से बाहर हटाइए और केंद्रीय पाद को वापस खींचिए।
• आइए, हम उत्तल पक्ष से गोले की त्रिज्या को मापने पर विचार करते हैं।
• अब स्केल और पेंच शीर्ष को पढ़िए। यदि पाठ्यांक 2 और 0.155 है, तो कुल पाठ्यांक 2.155 होगा।
• यदि पाठ्यांक शून्य रेखाओं के नीचे है, तो पाठ्यांक को शून्यांक त्रुटि में जोड़ा जाना चाहिए। यदि पाठ्यांक शून्य रेखाओं के ऊपर है, तो पाठ्यांक को शून्यांक त्रुटि से घटाया जाना चाहिए।
• दो पादों के बीच की लंबाई को मापने के लिए, उपकरण को समतल कार्ड पर रखिए और मीटर स्केल का उपयोग करके लंबाई को मापिए।
• निम्नलिखित समीकरण का उपयोग करके वक्रता त्रिज्या की गणना की जा सकती है:

स्फेरोमीटर का अल्पतमांक क्या है?

निम्न संबंध का उपयोग करके अल्पतमांक (L.C.) की गणना की जा सकती है:

स्फेरोमीटर का पिच: पिच को मुख्य स्केल के अनुदिश एक पूर्ण घूर्णन में वृत्ताकार चकती द्वारा तय की गई दूरी के रूप में परिभाषित किया जाता है। इसलिए, स्फेरोमीटर का पिच 1 mm = 0.1 cm के रूप में दिया जाता है।

वृत्तीय भागों की संख्या = 100

इसलिए,

स्फेरोमीटर में शून्यांक त्रुटि क्या है?

शून्यांक त्रुटि आपके पाठ्यांक में वह त्रुटि है जो तब निर्धारित की जाती है, जब आपका उपकरण शून्य मान के स्थान पर कोई शून्येतर मान पढ़ता है।

स्फेरोमीटर में शून्यांक त्रुटि नहीं है क्योंकि प्राप्त परिणाम अंतिम और प्रारंभिक पाठ्यांकों के बीच का अंतर होता है।

स्फेरोमीटर के उपयोग

स्फेरोमीटर या गोलाईमापी का उपयोग प्रकाशिक लेंस, गोलीय दर्पण और गेंद जैसी गोलीय सतहों की वक्रता त्रिज्या को मापने के लिए किया जाता है। इन छोटे, उच्च यथार्थता वाले प्रकाशिक परीक्षण उपकरणों का उपयोग सूक्ष्मदर्शी स्लाइड की मोटाई या स्लाइड गर्तों की गहराई को मापने के लिए भी किया जाता है।

स्फेरोमीटर के लिए हल किए गए उदाहरण

उदाहरण-1 एक छात्र एक स्फेरोमीटर का उपयोग करके उत्तल दर्पण की ऊंचाई h को मापता है। स्फेरोमीटर के पाद एक-दूसरे से 4 cm की दूरी पर हैं, और इसके रैखिक स्केल पर प्रति cm दस भाग हैं, और वृत्तीय स्केल में 50 भाग हैं। छात्र 2 को रैखिक स्केल के भाग के रूप में और 40 को वृत्तीय स्केल के भाग के रूप में लेता है। उत्तल दर्पण की वक्रता त्रिज्या क्या है?

हल:

उदाहरण-2 स्फेरोमीटर द्वारा मापी जाने वाली एक अवतल दर्पण की वक्रता त्रिज्या निम्न द्वारा दी जाती है:

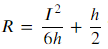
I और h के मान क्रमश: 4 cm और 0.065 cm हैं, जहाँ ‘I’ को एक मीटर स्केल द्वारा और h को एक स्फेरोमीटर द्वारा मापा जाता है। R के मापन में आपेक्षिक त्रुटि ज्ञात कीजिए।

हल:

स्फेरोमीटर या गोलाईमापी प्रयोग

प्रयोग शीर्षक – वक्रता त्रिज्या ज्ञात करने के लिए स्फेरोमीटर का उपयोग

प्रयोग विवरण – एक स्फेरोमीटर एक परिशुद्ध उपकरण है, जो बहुत छोटी लंबाई को मापता है। आइए एक स्फेरोमीटर का उपयोग करके दिए गए गोलीय पृष्ठ की वक्रता त्रिज्या निर्धारित करते हैं।

प्रयोग का उद्देश्य – एक स्फेरोमीटर द्वारा किसी दिए गए गोलीय पृष्ठ की वक्रता त्रिज्या को निर्धारित करना। 

आवश्यक सामग्री – एक स्फेरोमीटर, एक उत्तल कांच का पृष्ठ, समतल कांच की एक प्लेट, एक पेंसिल, एक मापक स्केल, कागज की एक शीट और कागज का एक छोटा टुकड़ा।

प्रक्रिया –

1. दिए गए स्फेरोमीटर का निरीक्षण कीजिए और इसके पिच स्केल के एक भाग के मान को नोट कीजिए।

2. वृत्तीय स्केल का निरीक्षण कीजिए और इस पर भागों की संख्या को नोट कीजिए।

3. स्फेरोमीटर का अल्पतमांक (L.C.) और पिच निर्धारित कीजिए। दी गई समतल कांच की प्लेट को एक क्षैतिज तल पर रखिए और उस पर स्फेरोमीटर को इस प्रकार रखिए कि इसके तीन पाद प्लेट पर विरामावस्था में हो।

4. कागज की एक शीट लीजिए, उस पर स्फेरोमीटर रखिए, और तीनों पादों के शीर्षों की छाप लेने के लिए इसे धीरे से दबाइए। तीनों छापों को मिलाकर एक समबाहु त्रिभुज ABC बनाइए और ΔABC की सभी भुजाओं को मापिए। दो स्फेरोमीटर पादों के बीच की माध्य दूरी, l ज्ञात कीजिए।
लंबाई l मापने में बहुत सावधानी बरतें क्योंकि l² पद का उपयोग दी गई गोलीय पृष्ठ की वक्रता R निर्धारित करने के लिए किया जाता है।

5. दिए गए गोलीय पृष्ठ को समतल कांच की प्लेट पर रखिए और फिर केंद्रीय पेंच को पर्याप्त ऊपर उठाकर उस पर स्फेरोमीटर रखिए, ताकि स्फेरोमीटर के तीन पाद गोलीय पृष्ठ पर टिके रहें, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

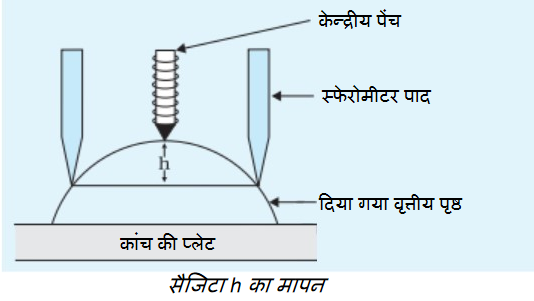
6. केंद्रीय पेंच को तब तक घुमाएं जब तक कि इसका निचला सिरा गोलीय पृष्ठ को धीरे से स्पर्श न कर ले। यह सुनिश्चित करने के लिए कि पेंच पृष्ठ को स्पर्श करता है, नीचे की सतह से परावर्तन के कारण निर्मित पेंच के प्रतिबिंब का निरीक्षण कीजिए।

7. पिच स्केल के पाठ्यांक और वृत्तीय स्केल के भागों का अवलोकन कीजिए, जो स्फेरोमीटर पाठ्यांक h लेने के लिए पिच स्केल के साथ रेखा में है प्रेक्षण सारणी में प्रेक्षणों को दर्ज कीजिए।

8. गोलीय पृष्ठ को हटाकर स्फेरोमीटर को समतल काँच की प्लेट पर रख दीजिए। केंद्रीय पेंच को तब तक घुमाएं जब तक कि इसका निचला सिरा कांच की प्लेट को धीरे से स्पर्श न कर जाए। फिर से, स्फेरोमीटर का पाठ्यांक h₂ लीजिए और इसे प्रेक्षण सारणी में रिकॉर्ड कीजिए। h₁ और h₂ के बीच का अंतर सैजिटा (h) के मान के बराबर है।

9. गोलीय पृष्ठ को इसके केंद्र में बिना कोई परिवर्तन किए तीन बार घुमा कर (5) से (8) तक चरणों की पुनरावृत्ति कीजिए। h का माध्य मान ज्ञात कीजिए।

सावधानियां –

1. स्फेरोमीटर के पेंच में घर्षण हो सकता है।
2. स्फेरोमीटर में पश्च त्रुटि हो सकती है।

स्फेरोमीटर पर अक्सर पूछे जाने वाले प्रश्न