1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿಯೊಂದಿಗೆ ಪ್ರಮಾಣಿತ ಟೆಸ್ಟ್ಗಳಲ್ಲಿ ವಿದ್ಯಾರ್ಥಿಗಳ ಸ್ಕೋರ್ಗಳನ್ನು ಊಹಿಸುವುದು
Embibe ನಲ್ಲಿ ಕಲಿಕೆಯ ಸಿದ್ಧಾಂತ ಮತ್ತು ಶಿಕ್ಷಣ ಸಂಶೋಧನೆಯಿಂದ ಒಳನೋಟಗಳು ಮತ್ತು ಮಾದರಿಗಳನ್ನು ಸಂಯೋಜಿಸುವ ಮೂಲಕ ಪ್ರಮಾಣಿತ ಪರೀಕ್ಷೆಗಳಲ್ಲಿ ವಿದ್ಯಾರ್ಥಿಗಳು ತಮ್ಮ ಅಂಕಗಳನ್ನು ಸುಧಾರಿಸಲು, ನಾವು ಸಹಾಯ ಮಾಡುತ್ತೇವೆ.
ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುವ ಅಂತಹ ಮಾದರಿಯ ಹೆಸರು ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ[1, 2], ವಿದ್ಯಾರ್ಥಿಯ ಕೌಶಲ್ಯ ಅಥವಾ ಸಾಮರ್ಥ್ಯದ ಮಟ್ಟ ಹಾಗೂ ಪ್ರಯತ್ನಿಸುತ್ತಿರುವ ಪ್ರಶ್ನೆಯ ಕ್ಲಿಷ್ಟತೆಯ ಮಟ್ಟವನ್ನು ಅಂದಾಜು ಮಾಡುವ ಮೂಲಕ, ಪ್ರಶ್ನೆಗೆ ಸರಿಯಾಗಿ ಉತ್ತರಿಸುವ ವಿದ್ಯಾರ್ಥಿಯ ಸಾಧ್ಯತೆಯನ್ನು ಊಹಿಸುತ್ತದೆ. ಇದನ್ನು ಮೊದಲು 1960 ರ ದಶಕದಲ್ಲಿ ಪ್ರಸ್ತಾಪಿಸಲಾಯಿತು ಮತ್ತು 1PL ಮಾದರಿ[2, 3 ] ಮತ್ತು 2PL[2,] ಮಾದರಿಯಂತಹ ಅನೇಕ ರೂಪಾಂತರಗಳು ಇಂದು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ.
ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿಯ 1PL ಮಾದರಿ
1PL ಅಥವಾ 1 ಪ್ಯಾರಾಮೀಟರ್ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿ, ಇದನ್ನು ರಾಶ್ ಮಾಡೆಲ್[3] ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ, ಇದನ್ನು ಈ ಕೆಳಗಿನಂತೆ ವಿವರಿಸಲಾಗಿದೆ.
i ನ್ನು ಶಿಕ್ಷಣಾರ್ಥಿ ಅಥವಾ ವಿದ್ಯಾರ್ಥಿ, j ಯು ಒಂದು ಪ್ರಶ್ನೆ ಎಂದುಕೊಳ್ಳೋಣ. θi ಶಿಕ್ಷಣಾರ್ಥಿಯ ಸಾಮರ್ಥ್ಯ ಮತ್ತು βj ಪ್ರಶ್ನೆಯ ಕ್ಲಿಷ್ಟತೆಯ ಮಟ್ಟವಾಗಿರಲಿ. ನಂತರ 1PL ಮಾದರಿಯ ಪ್ರಕಾರ, j ನೇ ಪ್ರಶ್ನೆಗೆ ಸರಿಯಾಗಿ ಉತ್ತರಿಸುವ i ಬಳಕೆದಾರರ ಸಂಭವನೀಯತೆ Pij ಅನ್ನು logit(Pij) = i – j ಎಂದು ನೀಡಲಾಗಿದೆ, ಅಲ್ಲಿ logit ಕಾರ್ಯವನ್ನು logit(x) =(1+(-x))-1 ಮೂಲಕ ನೀಡಲಾಗುತ್ತದೆ.
1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿಯನ್ನು ಬಳಸಿಕೊಂಡು, ಪ್ರತಿ ಪ್ರಯತ್ನದ ಪ್ರಶ್ನೆಗೆ ಶಿಕ್ಷಣಾರ್ಥಿಗಳ ಪ್ರತಿಕ್ರಿಯೆಯ ಡೇಟಾವನ್ನು ನೀಡಲಾಗಿದೆ, ಇದರಿಂದ ನಾವು ಶಿಕ್ಷಣಾರ್ಥಿಗಳ ಸಾಮರ್ಥ್ಯದ ಮಟ್ಟ θi ಅನ್ನು ಊಹಿಸಬಹುದು.
1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿಗಾಗಿ ಆಳವಾದ ಕಲಿಕೆಯ ವಿನ್ಯಾಸ
1PL ಮಾದರಿಯು ಡೊಮೇನ್-ನಿರ್ದಿಷ್ಟ ನಿಯತಾಂಕಗಳೊಂದಿಗೆ ಲಾಜಿಸ್ಟಿಕ್ ರಿಗ್ರೆಷನ್ ಎಂದು ನಾವು ನೋಡಬಹುದು. ಪರಿಣಾಮವಾಗಿ, ಯಾವುದೇ ಆಳವಾದ ಕಲಿಕೆಯ ಚೌಕಟ್ಟನ್ನು ಬಳಸಿಕೊಂಡು ನಾವು ಅಂತಹ ಮಾದರಿಯನ್ನು ಅರಿತುಕೊಳ್ಳಬಹುದು. 1PL ಮಾದರಿಯ ಆಳವಾದ ಕಲಿಕೆಯ ವಾಸ್ತುಶಿಲ್ಪವನ್ನು ಚಿತ್ರ 1 ರಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ.
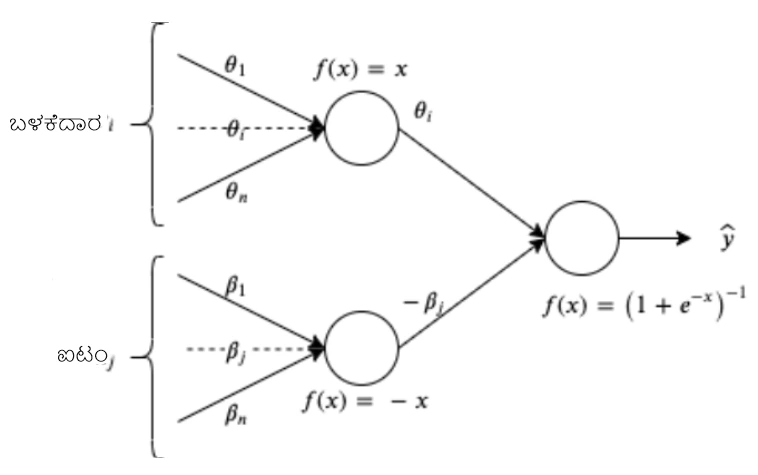
ಚಿತ್ರ 1: 1PL IRT ಮಾದರಿ ನಿಯತಾಂಕಗಳನ್ನು ಅಂದಾಜು ಮಾಡಲು ನ್ಯೂರಲ್ ನೆಟ್ವರ್ಕ್ ವಿನ್ಯಾಸ
ನಮ್ಮ ಮಾದರಿಯನ್ನು ಕೆರಾಸ್[4]ನಲ್ಲಿ ಆಳವಾದ ನ್ಯೂರಲ್ ನೆಟ್ವರ್ಕ್ ಮೂಲಕ ಅಳವಡಿಸಲಾಗಿದೆ. ನ್ಯೂರಲ್ ನೆಟ್ವರ್ಕ್ ರೀತಿಯಲ್ಲಿ ಸಮಸ್ಯೆಯನ್ನು ಮಾದರಿಯಾಗಿ ಮಾಡುವ ಅನುಕೂಲಗಳು:
- ಇನ್ಪುಟ್ನಲ್ಲಿ ಬಿಟ್ಟುಹೋಗಿರುವ ಮೌಲ್ಯಗಳನ್ನು ನಿರ್ವಹಿಸುವ ಸಾಮರ್ಥ್ಯ — ಪ್ರತಿಯೊಬ್ಬ ಬಳಕೆದಾರರು ಪ್ರತಿ ಪ್ರಶ್ನೆಯನ್ನು ಪ್ರಯತ್ನಿಸುವ ಅಗತ್ಯವಿಲ್ಲ
- ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಬಳಕೆದಾರರು ಮತ್ತು ಐಟಂಗಳನ್ನು ಅಳೆಯುವ ಸಾಮರ್ಥ್ಯ
- 2PL, 3PL ಮತ್ತು ಇತರೆ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿಯ ಮಾದರಿಗಳ ಚೌಕಟ್ಟನ್ನು ಹೆಚ್ಚಿನ ನಿಯತಾಂಕಗಳೊಂದಿಗೆ ವಿಸ್ತರಿಸುವ ಸಾಮರ್ಥ್ಯ
ನಾವು ಈ ಮಾದರಿಯನ್ನು 1PL ಆಳವಾದ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿ ಎಂದು ಉಲ್ಲೇಖಿಸುತ್ತೇವೆ.
ಮೌಲ್ಯೀಕರಣ
ಮಾದರಿಗೊಳಿಸುವಿಕೆಯ ತಂತ್ರವನ್ನು ಬೆಂಚ್ಮಾರ್ಕ್ ಮಾಡಲು ಮತ್ತು ಮೌಲ್ಯೀಕರಿಸಲು, ನಾವು ಈ ಕೆಳಗಿನಂತೆ ಸಿಮ್ಯುಲೇಟ್ ಆದ ಡೇಟಾವನ್ನು ರಚಿಸುತ್ತೇವೆ:
- i N(0,1) : ಸರಾಸರಿ 0 ಮತ್ತು ಪ್ರಮಾಣಿತ ವಿಚಲನ 1 ರೊಂದಿಗೆ ಸಾಮಾನ್ಯ ವಿತರಣೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಕಲಿಯುವ ಸಾಮರ್ಥ್ಯವನ್ನು ಉತ್ಪಾದಿಸಲಾಗುತ್ತದೆ
- j U(-1,1) : ಪ್ರಶ್ನೆಯ ತೊಂದರೆ ಮೌಲ್ಯಗಳನ್ನು -1 ಮತ್ತು 1 ರ ನಡುವೆ ಏಕರೂಪವಾಗಿ ರಚಿಸಲಾಗಿದೆ
- Pij= i - j : ಸರಿಯಾದ ಪ್ರತಿಕ್ರಿಯೆಗಳ ಸಂಭವನೀಯತೆಯನ್ನು ಬಳಕೆದಾರರ ಸಾಮರ್ಥ್ಯ ಮತ್ತು ಐಟಂ ತೊಂದರೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ (1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಸಮೀಕರಣವನ್ನು ಬಳಸಿಕೊಂಡು)
- yijk ಬರ್ನ್(Pij): ಬೈನರಿ ಪ್ರತಿಕ್ರಿಯೆಗಳನ್ನು ( ಸರಿಯಾದದ್ದು- ಸರಿಯಾಗಿ ಇಲ್ಲದೆ ಇರುವಂತದ್ದು) ಬರ್ನೌಲಿ ಹಂಚಿಕೆಯಿಂದ ಯಶಸ್ಸಿನ ಸಂಭವನೀಯತೆ Pij ನೊಂದಿಗೆ ಮಾದರಿ ಮಾಡಲಾಗುತ್ತದೆ, ಇಲ್ಲಿ ಪ್ರತಿ ವಿದ್ಯಾರ್ಥಿಗೆ ಪ್ರತಿ ಐಟಂಗೆ ಪ್ರತಿಕ್ರಿಯೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ವಿನ್ಯಾಸ ಮಾಡಬಹುದಾಗಿದೆ.
ನಾವು 100 ಪ್ರಶ್ನೆಗಳನ್ನು ಸಿಮ್ಯುಲೇಟ್ ಮಾಡಿದ್ದೇವೆ, 100 ಜನ ಶಿಕ್ಷಣಾರ್ಥಿಗಳು ಮತ್ತು ಪ್ರತಿ ಪ್ರಶ್ನೆಗೆ ಪ್ರತಿ ಶಿಕ್ಷಣಾರ್ಥಿಗೆ ಒಂದು ಪ್ರತಿಕ್ರಿಯೆ.
ನಾವು 1PL ಆಳವಾದ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿಯನ್ನು ಅನುಕರಿಸಲಾದ ದತ್ತಾಂಶ ಗುಂಪಿಗೆ ಹೊಂದಿಸುತ್ತೇವೆ. ನ್ಯೂರಲ್ ನೆಟ್ವರ್ಕ್ ವ್ಯವಸ್ಥೆಗೆ ಇನ್ಪುಟ್ಗಳು ಬಳಕೆದಾರರ ವೆಕ್ಟರ್ (ಒಂದು-ಹಾಟ್ ಎನ್ಕೋಡ್) ಮತ್ತು ಪ್ರಶ್ನೆ ವೆಕ್ಟರ್ (ಒಂದು-ಹಾಟ್ ಎನ್ಕೋಡ್ ಕೂಡ), ಮತ್ತು ಔಟ್ಪುಟ್ಗಳು ಐಟಂ ಪ್ರತಿಕ್ರಿಯೆ ಸಿದ್ಧಾಂತದ ಮಾದರಿಯ ನಿಯತಾಂಕಗಳಾಗಿವೆ, ಇದರಲ್ಲಿ ಐಟಂ ಕಷ್ಟ, ಶಿಕ್ಷಣಾರ್ಥಿಗಳ ಸಾಮರ್ಥ್ಯ ಮತ್ತು ಶಿಕ್ಷಣಾರ್ಥಿ ಭವಿಷ್ಯದಲ್ಲಿ ಸರಿಯಾಗಿ ಉತ್ತರಿಸುತ್ತಾರೋ ಅಥವಾ ಇಲ್ಲವೋ ಎಂಬುದನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ. ನ್ಯೂರಲ್ ನೆಟ್ವರ್ಕ್ ಸಂಪೂರ್ಣವಾಗಿ ಸಂಪರ್ಕ ಹೊಂದಿರುತ್ತದೆ. ಇದು ಎರಡು ಇನ್ಪುಟ್ ಪದರಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಕಷ್ಟ ಮತ್ತು ಸಾಮರ್ಥ್ಯಕ್ಕಾಗಿ ಮಧ್ಯಂತರ ಪದರಗಳು ಮತ್ತು ಒಂದು ಸಂಭವನೀಯ ಔಟ್ಪುಟ್ ಪದರ.
ನಾವು ನ್ಯೂರಲ್ ನೆಟ್ವರ್ಕ್ನಿಂದ 1PL ಆಳವಾದ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಔಟ್ಪುಟ್ ಅನ್ನು ಸಿಮ್ಯುಲೇಟ್ ಆದ ಡೇಟಾದಿಂದ ನಿಜವಾದ ಔಟ್ಪುಟ್ಗಳೊಂದಿಗೆ ಹೋಲಿಸುತ್ತೇವೆ.
ಅನುಷ್ಠಾನ
ಮಾದರಿ: 1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿಯ ವಿನ್ಯಾಸವನ್ನು ಕೆರಾಸ್ ಕ್ರಿಯಾತ್ಮಕ API ಗಳನ್ನು ಬಳಸಿಕೊಂಡು NN ಗಳ ಸಂಯೋಜನೆಯನ್ನು ಬಳಸಿಕೊಳ್ಳುವ ಮೂಲಕ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ದಟ್ಟವಾದ ಪದರಗಳನ್ನು ಪೇರಿಸಿ ಒಟ್ಟಾರೆ ಮಾದರಿಯನ್ನು ರಚಿಸಲಾಗಿದೆ – ಇಲ್ಲಿ, 1PL ಮಾದರಿಗಾಗಿ 2 ದಟ್ಟವಾದ ಪದರಗಳು, ಬಳಕೆದಾರನ ಪ್ರತಿ ಪ್ರತಿನಿಧಿ ಅಥವಾ ಐಟಂ ನಿಯತಾಂಕಗಳು ಒಂದು ಐಟಂ (j) ಗೆ ಪ್ರತಿಕ್ರಿಯಿಸುವ ಬಳಕೆದಾರರ (i) ಸಂಭವನೀಯತೆಯನ್ನು ಚಾಲನೆ ಮಾಡುವಲ್ಲಿ ಪ್ರಮುಖವಾಗಿದೆ (Pij).
ಅಧಿಕ ನಿಯತಾಂಕಗಳು: ಕೆಳಗಿನ ಡೀಫಾಲ್ಟ್ ಸಂಯೋಜನೆಗಳನ್ನು ಪ್ರತಿ ದಟ್ಟವಾದ ಪದರದಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ
- ಕರ್ನಲ್ ಮತ್ತು ಬಯಾಸ್ ಪ್ರಾರಂಭಿಕಗಳು: ಸಾಮಾನ್ಯ (0,1)
- l1/l2 ಕ್ರಮಬದ್ಧಗೊಳಿಸುವಿಕೆಗಳು : l_1=0, l_2=0
- ಚಟುವಟಿಕೆ ಕ್ರಮಬದ್ಧಗೊಳಿಸುವಿಕೆಗಳು : l_1=0, l_2=0
ಮೇಲಿನ ಸಂಯೋಜನೆಗಳನ್ನು ಡೆವಲಪರ್ನಿಂದ ಅತಿಕ್ರಮಿಸಬಹುದು ಅಥವಾ ಸಂರಚನೆಗಳ ಜಾಗದಲ್ಲಿ ಹುಡುಕುವ ಮೂಲಕ ಉತ್ತಮ ಸಂರಚನೆಯನ್ನು ಪಡೆಯಬಹುದು. ಅಂತಹ ವಿವರಗಳು ಮುಂಬರುವ ಬ್ಲಾಗ್ ಆಗಿರುತ್ತದೆ. ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಮಾದರಿಯು ಅದರ ಬಳಕೆಯನ್ನು ಎರಡು ಅಥವಾ ಮೂರು ನಿಯತಾಂಕಗಳಿಗೆ ವಿಸ್ತರಿಸಲು ಸಾಕಷ್ಟು ಹೊಂದಿಕೊಳ್ಳುತ್ತದೆ, ಅವುಗಳೆಂದರೆ ತಾರತಮ್ಯ ಮತ್ತು ಊಹೆ, ಮತ್ತು ಪರಿಣಾಮವಾಗಿ ಸಿಂಹಾವಲೋಕನದಲ್ಲಿ, ನ್ಯೂರಲ್ ವಿನ್ಯಾಸದ ಹುಡುಕಾಟ ಸಾಮರ್ಥ್ಯದೊಂದಿಗೆ ವಿಸ್ತೃತ ಮಾದರಿಯನ್ನು ಒಂದು ಅಥವಾ ಎರಡು PL ಮಾದರಿಯಂತೆ ನಿರ್ವಹಿಸಲು ನಿರ್ಬಂಧಿಸಬಹುದು.
ಪ್ರಾಯೋಗಿಕ ಫಲಿತಾಂಶಗಳು
ಕೆಳಗಿನ ನಕ್ಷೆಗಳು ಇವುಗಳ ನಡುವಿನ ಪರಸ್ಪರ ಸಂಬಂಧವನ್ನು ತೋರಿಸುತ್ತವೆ:
- ಪಿಯರ್ಸನ್ ಪರಸ್ಪರ ಸಂಬಂಧ ಗುಣಾಂಕ 0.9857 ನೊಂದಿಗೆ ನಿಜವಾದ ಕ್ಲಿಷ್ಟತಾ ಮಟ್ಟಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ ಊಹಿಸಲಾದ ಕ್ಲಿಷ್ಟತೆಯಾಗಿದೆ.
- ಪಿಯರ್ಸನ್ ಪರಸ್ಪರ ಸಂಬಂಧ ಗುಣಾಂಕ 0.9954 ನೊಂದಿಗೆ ನಿಜವಾದ ಸಾಮರ್ಥ್ಯದ ಮಟ್ಟಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ ಊಹಿಸಲಾದ ಸಾಮರ್ಥ್ಯ.
- ಪಿಯರ್ಸನ್ ಪರಸ್ಪರ ಸಂಬಂಧ ಗುಣಾಂಕ 0.9926 ನೊಂದಿಗೆ ಪ್ರತಿ ಪ್ರಶ್ನೆಗೆ ಸರಿಯಾಗಿ ಉತ್ತರಿಸುವ ಸಂಭವನೀಯತೆ ಮತ್ತು ನಿಜವಾದ ಸಂಭವನೀಯತೆ.
1PL ಡೇಟಾದಲ್ಲಿ ತರಬೇತಿ ಪಡೆದ ಆಳವಾದ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿಯಿಂದ, 1PL DIRT ಮಾದರಿಯ ಕೋಷ್ಟಕ ಸಂಭವನೀಯತೆ 0.587 ಆಗಿದೆ.
ನಾವು ನೋಡಿದಂತೆ, ನಮ್ಮ 1PL ಆಳವಾದ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿಯು ಕ್ಲಿಷ್ಟತೆ, ಸಾಮರ್ಥ್ಯವನ್ನು ಮತ್ತು ಟೆಸ್ಟ್ ಸ್ಕೋರ್ ಅನ್ನು ನಿಖರವಾಗಿ ಊಹಿಸುವಲ್ಲಿ ಯಶಸ್ವಿಯಾಗಿದೆ, ಎಲ್ಲಾ ಮೂರು ಸಂದರ್ಭಗಳಲ್ಲಿ ನಾವು ಪರಸ್ಪರ ಸಂಬಂಧವನ್ನು ಉತ್ತಮವಾಗಿ ಹೊಂದುತ್ತೇವೆ ಎಂದು ಸೂಚಿಸುತ್ತದೆ.
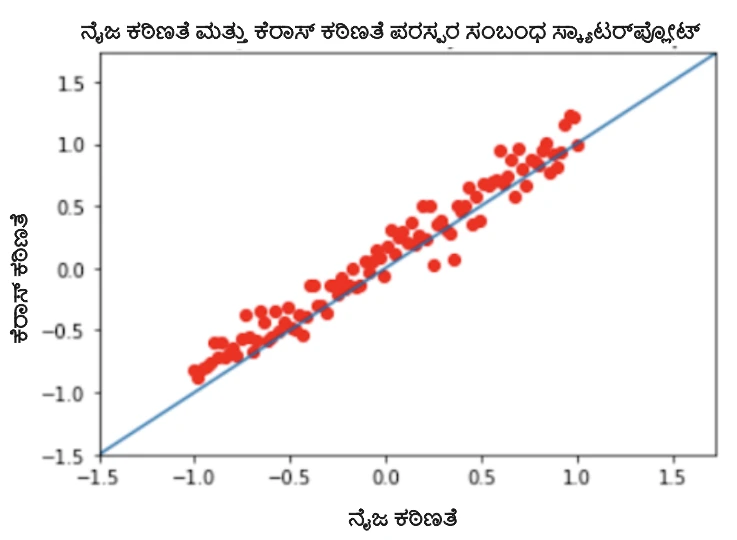
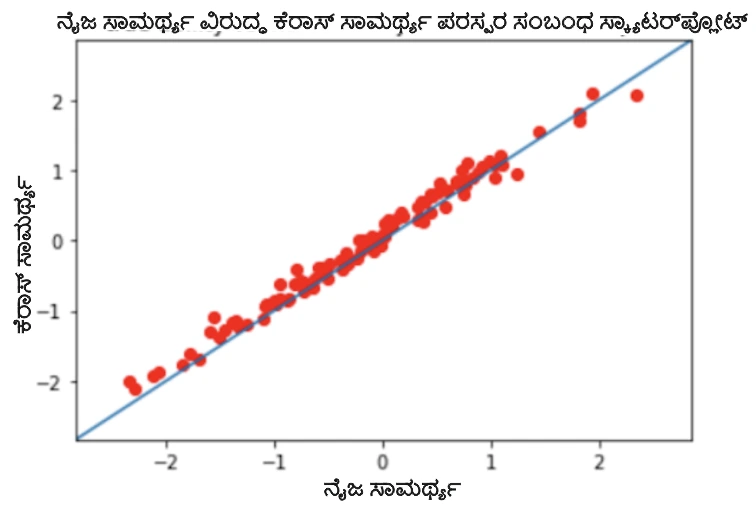
ಚಿತ್ರ 2: ನಿಜವಾದ ಮತ್ತು ಕೆರಾಸ್ ನಡುವಿನ ಮಾದರಿಯ ತೊಂದರೆ ಮತ್ತು ಸಾಮರ್ಥ್ಯದ ನಿಯತಾಂಕಗಳ ಸ್ಕ್ಯಾಟರ್ಪ್ಲಾಟ್ಗಳು
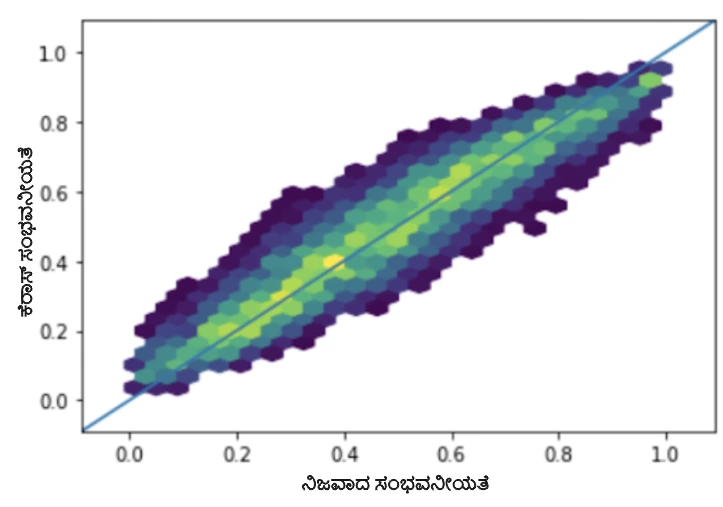
ಚಿತ್ರ 3: ಪ್ರಶ್ನೆಗಳಿಗೆ ಸರಿಯಾಗಿ ಉತ್ತರಿಸುವ ನಿಜವಾದ ಸಂಭವನೀಯತೆಯ ಎದುರಾಗಿ ನಮ್ಮ ತರಬೇತಿ ಪಡೆದ ಕೆರಾಸ್ ಮಾದರಿಯಿಂದ ಪಡೆದ ಸಂಭವನೀಯತೆಯ ಹೆಕ್ಸ್ಬಿನ್ ನಕ್ಷೆ
ನಿರ್ಣಯ
ಸಿಮ್ಯುಲೇಶನ್ಗಳ ಆಧಾರದ ಮೇಲೆ, 1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಮಾದರಿಯನ್ನು ಆಳವಾದ ಕಲಿಕೆಯ ಮಾದರಿಯ ಮೂಲಕ ಕಾರ್ಯಗತಗೊಳಿಸಬಹುದು ಎಂದು ನಾವು ತೋರಿಸಿದ್ದೇವೆ. ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ನಿಯತಾಂಕಗಳನ್ನು ಬಳಸಿಕೊಂಡು, 1PL ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ ಆಧಾರಿತ ಮಾದರಿಯನ್ನು ಬಳಸಿಕೊಂಡು ನಮ್ಮ ಕಲಿಕಾ ಸಾಮರ್ಥ್ಯ ಮತ್ತು ಕಷ್ಟಕರ ಪ್ರಶ್ನೆಗಳ ಮಟ್ಟವನ್ನು ನಾವು ಉತ್ತಮವಾಗಿ ಅಂದಾಜಿಸಬಹುದು. ಅಡಾಪ್ಟಿವ್ ಟೆಸ್ಟ್ಗಳನ್ನು ರಚಿಸಲು, ಗುರಿ ನಿರ್ಧರಿಸಲು ಮತ್ತು ಇತರ ಕೆಳಹಂತದ ಸಮಸ್ಯೆಗಳನ್ನು ಅಂದಾಜಿಸಲು ಇದನ್ನು ಬಳಸಬಹುದು.
ಉಲ್ಲೇಖಗಳು:
- “ಫ್ರಾಂಕ್ ಬಿ. ಬೇಕರ್. “ದಿ ಬೇಸಿಕ್ಸ್ ಆಫ್ ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ.” ERIC, USA, 2001
- ವಿಕಿಪೀಡಿಯಾ. ಐಟಂ ರೆಸ್ಪಾನ್ಸ್ ಥಿಯರಿ https://en.wikipedia.org/wiki/Item_response_theory
- ಜಾರ್ಜ್ ರಾಶ್. “ಸ್ಟಡೀಸ್ ಇನ್ ಮ್ಯಾಥಮೆಟಿಕಲ್ ಸೈಕಾಲಜಿ: I. ಪ್ರಾಬಬಿಲಿಸ್ಟಿಕ್ ಮೋಡೆಲ್ಸ್ ಫಾರ್ ಸಮ್ ಇಂಟೆಲಿಜೆನ್ಸ್ ಅಂಡ್ ಅಟ್ಟಿಂಮೆಂಟ್ ಟೆಸ್ಟ್ಸ್.” 1960.
- ಕೇರಸ್ ಡೀಪ್ ಲರ್ನಿಂಗ್ ಫ್ರೇಮ್ವರ್ಕ್: ಕೇರಾಸ್”