1PL ഐറ്റത്തിൻ്റെ റെസ്പോൺസ് സിദ്ധാന്തം ഉപയോഗിച്ച് സ്റ്റാൻഡേർഡ് ടെസ്റ്റുകളിൽ വിദ്യാർത്ഥികളുടെ സ്‌കോറുകൾ പ്രവചിക്കുന്നു

Embibe-ൽ, പഠന സിദ്ധാന്തം, വിദ്യാഭ്യാസ ഗവേഷണം എന്നിവയിൽ നിന്നുള്ള ഉൾക്കാഴ്‌ചകളും മാതൃകകളും ഉൾപ്പെടുത്തി, സ്റ്റാൻഡേർഡ് പരീക്ഷകളിൽ അവരുടെ സ്‌കോർ മെച്ചപ്പെടുത്താൻ ഞങ്ങൾ വിദ്യാർത്ഥികളെ സഹായിക്കുന്നു.

ഐറ്റം റെസ്‌പോൺസ് തിയറി[1, 2] എന്ന പേരിൽ വ്യാപകമായി ഉപയോഗിക്കപ്പെടുന്ന ഒരു മോഡൽ, വിദ്യാർത്ഥിയുടെ വൈദഗ്ധ്യം അല്ലെങ്കിൽ കഴിവ് നിലയും അതുപോലെ പരീക്ഷിക്കപ്പെടുന്ന ചോദ്യത്തിന്റെ ബുദ്ധിമുട്ട് നിലയും കണക്കാക്കി, ഒരു ചോദ്യത്തിന് ശരിയായി ഉത്തരം നൽകാനുള്ള വിദ്യാർത്ഥിയുടെ സാധ്യത പ്രവചിക്കുന്നു. 1960-കളിൽ ഇത് ആദ്യമായി നിർദ്ദേശിക്കപ്പെട്ടു, 1PL മോഡൽ[2, 3], 2PL മോഡൽ[2] പോലെയുള്ള പല വകഭേദങ്ങളും ഇന്ന് നിലവിലുണ്ട്.

ഐറ്റം റെസ്പോൺസ് സിദ്ധാന്തത്തിന്റെ 1PL മോഡൽ

റാഷ് മോഡൽ[3] എന്നും അറിയപ്പെടുന്ന 1PL അല്ലെങ്കിൽ 1 പാരാമീറ്റർ ഐറ്റം റെസ്‌പോൺസ് തിയറി മോഡൽ ഇനി പറയുന്ന രീതിയിൽ വിവരിച്ചിരിക്കുന്നു.

 i ഒരു പഠിതാവോ വിദ്യാർത്ഥിയോ ആകട്ടെ, j ഒരു ചോദ്യമാകട്ടെ. θi എന്നത് പഠിതാവിന്റെ കഴിവും βj എന്നത് ചോദ്യത്തിന്റെ ബുദ്ധിമുട്ട് ലെവലും ആകട്ടെ. തുടർന്ന് 1PL മോഡൽ അനുസരിച്ച്, jth ചോദ്യത്തിന് ശരിയായി ഉത്തരം നൽകുന്ന ith ഉപയോക്താവിന്റെ പ്രോബബിലിറ്റി Pij logit(Pij) = i – j എന്ന് നൽകിയിരിക്കുന്നു, അവിടെ ലോജിറ്റ് ഫംഗ്ഷൻ ലോജിറ്റ്(x) =(1+(-x)) -1 നൽകുന്നു. 

1PL ഐറ്റം റെസ്‌പോൺസ് തിയറി മോഡൽ ഉപയോഗിച്ച്, പരീക്ഷിച്ച ഓരോ ചോദ്യത്തിനും പഠിതാവിന്റെ പ്രതികരണത്തെക്കുറിച്ചുള്ള ഡാറ്റ നൽകി, ഒരു പഠിതാവിന്റെ കഴിവ് ലെവൽ θi നമുക്ക് പ്രവചിക്കാൻ കഴിയും.

1PL ഐറ്റം റെസ്പോൺസ് സിദ്ധാന്തത്തിനായുള്ള ആഴത്തിലുള്ള പഠന ആർക്കിടെക്ചർ

ഒരു ഡൊമെയ്ൻ-നിർദ്ദിഷ്‌ട പാരാമീട്രൈസേഷൻ ഉള്ള 1PL മോഡൽ തീർച്ചയായും ലോജിസ്റ്റിക് റിഗ്രഷൻ ആണെന്ന് നമുക്ക് കാണാൻ കഴിയും. തൽഫലമായി, ഏതെങ്കിലും ആഴത്തിലുള്ള പഠന ചട്ടക്കൂട് ഉപയോഗിച്ച് നമുക്ക് അത്തരമൊരു മാതൃക തിരിച്ചറിയാൻ കഴിയും. 1PL മോഡലിനായുള്ള ആഴത്തിലുള്ള പഠന വാസ്തുവിദ്യ ചിത്രം 1 ൽ കാണിച്ചിരിക്കുന്നു.

 

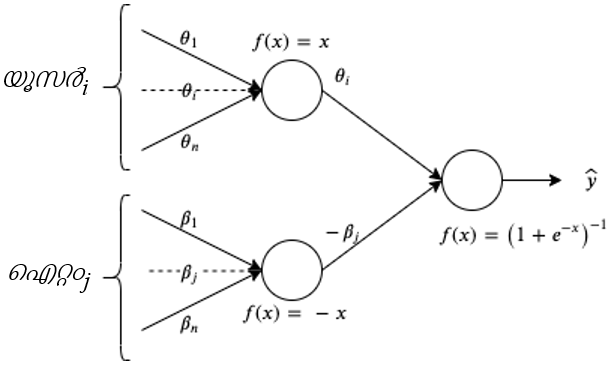
ഞങ്ങളുടെ മാതൃക കേരാസിൽ[4] ഒരു ആഴത്തിലുള്ള ന്യൂറൽ നെറ്റ്‌വർക്ക് ആയി നടപ്പിലാക്കുന്നു. ഒരു ന്യൂറൽ നെറ്റ്‌വർക്ക് എന്ന നിലയിൽ പ്രശ്നത്തെ മാതൃകയാക്കുന്നതിന്റെ ഗുണങ്ങൾ ഇവയാണ്:

• ഇൻപുട്ടിൽ നഷ്ടപ്പെട്ട മൂല്യങ്ങൾ കൈകാര്യം ചെയ്യാനുള്ള കഴിവ് — ഓരോ യൂസറും ഓരോ ചോദ്യവും ശ്രമിക്കേണ്ടതില്ല
• ധാരാളം യൂസറുകളിലേക്കും ഇനങ്ങളിലേക്കും സ്കെയിൽ ചെയ്യാനുള്ള കഴിവ്
• കൂടുതൽ പാരാമീറ്ററുകളുള്ള 2PL, 3PL, മറ്റ് ഐറ്റം റെസ്‌പോൺസ് തിയറി മോഡലുകളിലേക്ക് ചട്ടക്കൂട് വിപുലീകരിക്കാനുള്ള കഴിവ്

ഞങ്ങൾ ഈ മോഡലിനെ 1PL ഡീപ് ഇനം റെസ്‌പോൺസ് തിയറി മോഡൽ എന്ന് വിളിക്കുന്നു.

മൂല്യനിർണ്ണയം

മോഡലിംഗ് തന്ത്രം മാനദണ്ഡമാക്കുന്നതിനും സാധൂകരിക്കുന്നതിനും, ഞങ്ങൾ ഇനി പറയുന്ന രീതിയിൽ സിമുലേറ്റഡ് ഡാറ്റ സൃഷ്ടിക്കുന്നു:

• i N(0,1) : ശരാശരി 0 ഉം സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ 1 ഉം ഉള്ള ഒരു സാധാരണ ഡിസ്ട്രിബ്യൂഷൻ ഉപയോഗിച്ചാണ് പഠിതാവിന്റെ കഴിവ് സൃഷ്ടിക്കുന്നത്.
• j U(-1,1) : ചോദ്യ വൈഷമ്യ മൂല്യങ്ങൾ -1 നും 1 നും ഇടയിൽ ഒരേപോലെ സൃഷ്ടിക്കപ്പെടുന്നു
• Pij= i ​​- j : യൂസറിന്റെ കഴിവും ഐറ്റത്തിന്റെ ബുദ്ധിമുട്ടും (1PL ഐറ്റം റെസ്‌പോൺസ് തിയറി സമവാക്യം ഉപയോഗിച്ച്) ഉപയോഗിച്ച് ശരിയായ പ്രതികരണങ്ങളുടെ സംഭാവ്യത കണക്കാക്കുന്നു.
• yijk Bern(Pij): ബൈനറി റെസ്പോൺസുകൾ (ശരിയായത്, ശരിയല്ല) Bernulli വിതരണത്തിൽ നിന്ന് വിജയ സാധ്യതയുള്ള Pij-ൽ നിന്ന് സാമ്പിൾ ചെയ്യുന്നു, ഇവിടെ ഓരോ പഠിതാവിനും ഓരോ ഐറ്റത്തിനും റെസ്പോൺസുകളുടെ എണ്ണം കോൺഫിഗർ ചെയ്യാവുന്നതാണ്.

ഓരോ ചോദ്യത്തിനും 100 ചോദ്യങ്ങൾ, 100 പഠിതാക്കൾ, ഒരു പഠിതാവിന് ഒരു റെസ്പോൺസ് എന്നിങ്ങനെ ഞങ്ങൾ അനുകരിച്ചിട്ടുണ്ട്.

സിമുലേറ്റഡ് ഡാറ്റാസെറ്റിലേക്ക് ഞങ്ങൾ 1PL ഡീപ്  ഐറ്റം റെസ്‌പോൺസ് തിയറി മോഡൽ ഉൾക്കൊള്ളുന്നു. ന്യൂറൽ നെറ്റ്‌വർക്കിലേക്കുള്ള ഇൻപുട്ടുകൾ ഉപയോക്തൃ വെക്‌ടറും (വൺ-ഹോട്ട് എൻകോഡ് ചെയ്‌തത്) ചോദ്യ വെക്‌ടറും (ഒപ്പം-ഹോട്ട് എൻകോഡ് ചെയ്‌തതും) ആണ്, കൂടാതെ  ഐറ്റത്തിന്റെ ബുദ്ധിമുട്ട്, പഠിതാവിന്റെ കഴിവ്, പ്രവചനം എന്നിവ ഉൾപ്പെടെ  ഐറ്റം റെസ്‌പോൺസ് സിദ്ധാന്തത്തിന്റെ മാതൃകയുടെ പാരാമീറ്ററുകളാണ് ഔട്ട്‌പുട്ടുകൾ. പഠിതാവ് ശരിയായി ഉത്തരം നൽകും അല്ലെങ്കിൽ ഇല്ല. ന്യൂറൽ നെറ്റ്‌വർക്ക് പൂർണ്ണമായും ബന്ധിപ്പിച്ചിരിക്കുന്നു. ഇതിന് രണ്ട് ഇൻപുട്ട് ലെയറുകൾ ഉണ്ട്, ബുദ്ധിമുട്ടിനും കഴിവിനുമുള്ള ഇന്റർമീഡിയറ്റ് ലെയറുകൾ, പ്രവചനത്തിന് ഒരു ഔട്ട്പുട്ട് ലെയർ.

ന്യൂറൽ നെറ്റ്‌വർക്കിൽ നിന്നുള്ള 1PL ഡീപ് ഐറ്റം റെസ്‌പോൺസ് തിയറി ഔട്ട്‌പുട്ടും സിമുലേറ്റഡ് ഡാറ്റയിൽ നിന്നുള്ള യഥാർത്ഥ ഔട്ട്‌പുട്ടുകളും ഞങ്ങൾ താരതമ്യം ചെയ്യുന്നു.

നടപ്പിലാക്കൽ

മാതൃക: 1PL ഐറ്റം റെസ്‌പോൺസ് തിയറിയുടെ ആർക്കിടെക്ചർ നിർവചിക്കുന്നത്, കെരാസ് ഫങ്ഷണൽ API-കൾ ഉപയോഗിച്ചുകൊണ്ട്, NN-കളുടെ ഘടനാപരമായ ഗുണങ്ങൾ ഉപയോഗിച്ചാണ്. ഡെൻസ് ലെയറുകൾ അടുക്കി വച്ചാണ് മൊത്തത്തിലുള്ള മോഡൽ ക്രമീകരിച്ചിരിക്കുന്നത് – ഇവിടെ, 1PL മോഡലിന് 2 ഡെൻസ് ലെയറുകൾ, ഒരു ഉപയോക്താവിന്റെ ഓരോ പ്രതിനിധിയും അല്ലെങ്കിൽ ഇനത്തിന്റെ പാരാമീറ്ററുകൾ ഒരു ഇനത്തോട് (j) പ്രതികരിക്കുന്ന ഒരു ഉപയോക്താവിന്റെ ഡ്രൈവിംഗ് സാധ്യതയിൽ (Pij) സുപ്രധാനമാണ്.

ഹൈപ്പർ പാരാമീറ്ററുകൾ: ഓരോ ഡെൻസ് ലെയറിലും ഇനി പറയുന്ന സ്ഥിരസ്ഥിതി ക്രമീകരണങ്ങൾ ഉപയോഗിക്കുന്നു

• കേർണൽ & ബയസ് ഇനീഷ്യലൈസറുകൾ: നോർമൽ (0,1)
• l1/l2 റെഗുലറൈസേഷനുകൾ : l_1=0, l_2=0
• ആക്റ്റിവിറ്റി റെഗുലറൈസറുകൾ : l_1=0, l_2=0

മുകളിലുള്ള ക്രമീകരണങ്ങൾ ഒരു ഡെവലപ്പർക്ക് അസാധുവാക്കാം അല്ലെങ്കിൽ കോൺഫിഗറേഷനുകളുടെ ഒരു സ്ഥലത്ത് തിരയുന്നതിലൂടെ മികച്ച കോൺഫിഗറേഷൻ ലഭിക്കും. അത്തരം വിശദാംശങ്ങൾ വരാനിരിക്കുന്ന ഒരു ബ്ലോഗ് ആയിരിക്കും. നിർവചിക്കപ്പെട്ട മോഡൽ അതിന്റെ ഉപയോഗം രണ്ടോ മൂന്നോ പരാമീറ്ററുകൾ, അതായത് വിവേചനം, ഊഹക്കണക്കുകൾ എന്നിവയ്ക്ക് വിപുലീകരിക്കാൻ പര്യാപ്തമാണ്, തൽഫലമായി, ന്യൂറൽ ആർക്കിടെക്ചർ സെർച്ച് ശേഷിയുമായി ചേർന്ന് ഒരു വിപുലീകൃത മോഡൽ ഒന്നോ രണ്ടോ PL മോഡലായി പ്രവർത്തിക്കാനായി പരിമിതപ്പെടുത്താം.

പരീക്ഷണ ഫലങ്ങൾ

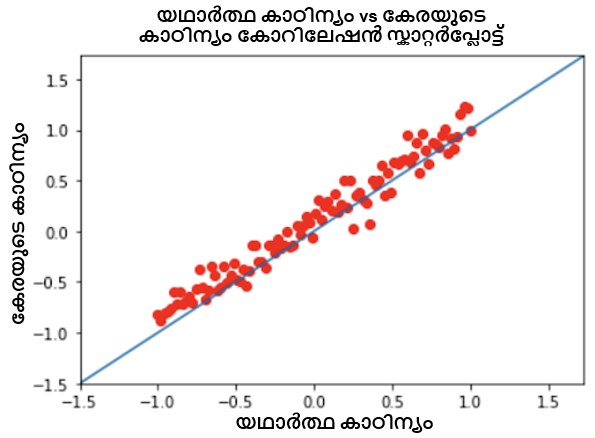
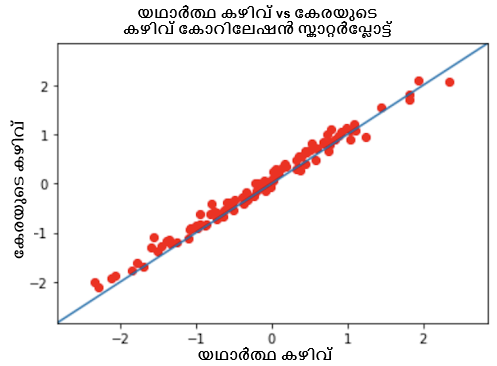
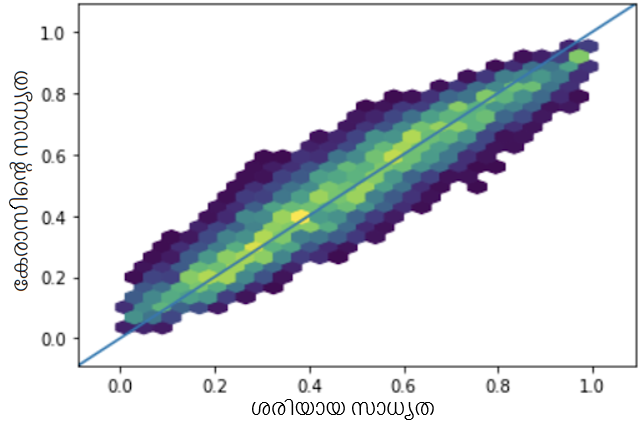
താഴെയുള്ള പ്ലോട്ടുകൾ ഇവ തമ്മിലുള്ള പരസ്പരബന്ധം കാണിക്കുന്നു:

• പിയേഴ്സൺ കോറിലേഷൻ കോഎഫിഷ്യന്റ് 0.9857 ഉള്ള പ്രവചിച്ച ബുദ്ധിമുട്ടും യഥാർത്ഥ ബുദ്ധിമുട്ട് നിലയും.
• പിയേഴ്സൺ കോറിലേഷൻ കോഎഫിഷ്യന്റ് 0.9954 ഉള്ള പ്രവചന ശേഷിയും യഥാർത്ഥ കഴിവ് നിലയും.
• പിയേഴ്സൺ കോറിലേഷൻ കോഎഫിഷ്യന്റ് 0.9926 ഉള്ള, ഓരോ ചോദ്യത്തിനും ശരിയായി ഉത്തരം നൽകാനുള്ള സാധ്യതയും യഥാർത്ഥ പ്രോബബിലിറ്റിയും.

1PL ഡാറ്റയിൽ പരിശീലിപ്പിച്ച ഡീപ് ഐറ്റം റെസ്പോൺസ് തിയറി മോഡലിൽ നിന്ന്, 1PL DIRT മോഡലിന്റെ ലോഗ് സാധ്യത 0.587 ആണ്.

നമുക്ക് കാണാനാകുന്നതുപോലെ, മൂന്ന് സാഹചര്യങ്ങളിലും ഞങ്ങൾക്ക് നല്ല പരസ്പരബന്ധം ലഭിക്കുന്നു, ഞങ്ങളുടെ 1PL ഡീപ് ഐറ്റം റെസ്‌പോൺസ് തിയറി മോഡൽ ബുദ്ധിമുട്ട്, കഴിവ്, ടെസ്റ്റ് സ്‌കോർ എന്നിവ നല്ല കൃത്യതയോടെ പ്രവചിക്കുന്നതിൽ വിജയിച്ചതായി സൂചിപ്പിക്കുന്നു.

ഉപസംഹാരം

സിമുലേഷനുകളെ അടിസ്ഥാനമാക്കി, ഒരു ഡീപ് ലേണിംഗ് മോഡൽ വഴി 1PL ഐറ്റം റെസ്‌പോൺസ് തിയറി മോഡൽ നടപ്പിലാക്കാൻ കഴിയുമെന്ന് ഞങ്ങൾ കാണിച്ചുതന്നു. ഐറ്റം റെസ്‌പോൺസ് തിയറി പാരാമീറ്ററുകൾ ഉപയോഗിച്ച്, ഞങ്ങളുടെ 1PL ഐറ്റം റെസ്‌പോൺസ് തിയറി അടിസ്ഥാനമാക്കിയുള്ള മോഡൽ ഉപയോഗിച്ച് പഠിതാവിന്റെ കഴിവിനെക്കുറിച്ചും ചോദ്യങ്ങളുടെ ബുദ്ധിമുട്ട് നിലയെക്കുറിച്ചും നല്ല കണക്കുകൾ നമുക്ക് ലഭിക്കും. അഡാപ്റ്റീവ് ടെസ്റ്റുകൾ, ഗോൾ ക്രമീകരണം, മറ്റ് ഡൗൺസ്ട്രീം പ്രശ്നങ്ങൾ എന്നിവ സൃഷ്‌ടിക്കുന്നതിന് ഈ കണക്കുകൾ ഉപയോഗിക്കാം

റഫറൻസുകൾ 

1. Frank B. Baker. “The basics of item response theory.” ERIC, USA, 2001
2. Wikipedia. Item Response Theory https://en.wikipedia.org/wiki/Item_response_theory
3. Georg Rasch. “Studies in mathematical psychology: I. Probabilistic models for some intelligence and attainment tests.” 1960.
4. Keras Deep Learning framework: Keras