ചോദ്യങ്ങൾക്ക് സ്വയ൦ ഉത്തരം നൽകാനുള്ള സോള്‍വര്‍ ടെക്നോളജി

നൂറുകണക്കിന് പരീക്ഷകളുടെ സിലബസിൽ നിന്ന് ആയിരക്കണക്കിന് ആശയങ്ങളിൽ ചോദ്യങ്ങൾ പ്രാക്ടീസ് ചെയ്യുന്നതിന് വിദ്യാർത്ഥികളെ അനുവദിക്കുന്ന ഒരു എഡ്‌ടെക് പ്ലാറ്റ്‌ഫോം ആണ് Embibe. ഒരു പ്രത്യേക ചോദ്യം എങ്ങനെ പരിഹരിക്കാമെന്ന് മനസ്സിലാക്കാൻ വിദ്യാർത്ഥികളെ സഹായിക്കുന്നതിനുള്ള വിശദീകരണങ്ങളും ഘട്ടം ഘട്ടമായുള്ള നിർധാരണ മാർഗ്ഗനിർദ്ദേശങ്ങളുമടങ്ങുന്ന സാങ്കേതികത Embibe സ്ഥാപിച്ചെടുത്തിട്ടുണ്ട്. വിഷയ വിദഗ്ധർ തന്നെ ചോദ്യങ്ങൾ നിർധാരണം ചെയ്യുന്ന ഒരു മാനുവൽ പ്രക്രിയയാണ് ഇത്.

Embibe ചോദ്യ ഡാറ്റാസെറ്റ് വിപുലീകൃതമാകുന്നതിനനുസരിച്ച്, സ്വയം സൃഷ്‌ടിച്ചെടുക്കുന്ന നിർധാരണങ്ങളെ ആശ്രയിക്കുന്നത് വളരെ ചെലവേറിയതാണ്. ഇൻ്റർമീഡിയറ്റ് ലെവൽ ഗണിതം പോലുള്ള ചില പ്രത്യേക വിഷയങ്ങളിൽ  പാഠ പുസ്തക ചോദ്യങ്ങൾ പരിഹരിക്കുന്നതിന് അൽഗോരിതം സൃഷ്‌ടിക്കുന്നതിൽ ഫലപ്രാപ്തി നേടിയിട്ടുള്ള  താരതമ്യേന നവീനമായ ഒരു മേഖലയാണ് സോൾവർ ടെക്‌നോളജി.

ധാരാളം ചോദ്യങ്ങൾക്കുള്ള ഉത്തരങ്ങളും ഘട്ടം ഘട്ടമായുള്ള പരിഹാരങ്ങളും സ്വയമേവ സൃഷ്ടിക്കുന്നതിനായി Embibe ഈ മേഖലയിൽ ഗവേഷണം നടത്തി ക്കൊണ്ടിരിക്കുന്നു.

പ്രശ്ന൦ ഉന്നയിക്കൽ 

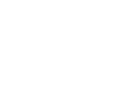
ഗണിതത്തിൻ്റെ ഒരു ടെക്‌സ്‌റ്റ് ചോദ്യം നൽകിയാൽ, സോൾവർ കോഡുകൾ ഉപയോഗിച്ച് അത് പരിഹരിച്ച് ഘട്ടം ഘട്ടമായുള്ള പരിഹാരം നൽകുക.

ചോദ്യം വിദ്യാർത്ഥിയിൽ നിന്നുള്ള ഏതെങ്കിലും സ്വതന്ത്രമായി നിർമ്മിച്ചെടുത്തതാകാം ,ഇത് പക്ഷെ  ഒരു പ്രത്യേക ഫോർമാറ്റിൽ ആയിരിക്കണമെന്നില്ല. ഞങ്ങൾ അത് പരിഹരിക്കാനും പരിഹാര ഘട്ടങ്ങൾ നൽകാനും ശ്രമിക്കുന്നു.

സമീപനം

മുഴുവൻ പ്രക്രിയയും എങ്ങനെ നടക്കുന്നുവെന്നത് ചുവടെ ചേർക്കുന്നു :

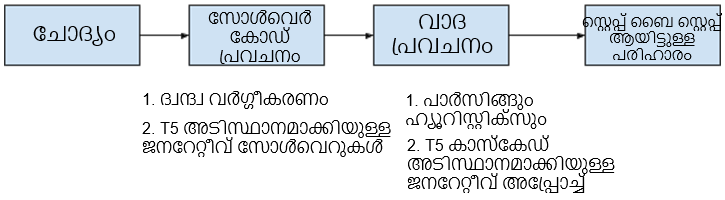
ഉദാഹരണത്തിന്,

സി.ബി.എസ്.ഇ  ആറാം ക്ലാസിലെ ഒരു ചോദ്യം ഇതാ:

“അക്കത്തിൽ എഴുതുക – രണ്ട് ലക്ഷത്തി അൻപതിനായിരത്തി തൊള്ളായിരത്തി മുപ്പത്തിയാറ്.”

അതിനാൽ, ആദ്യ ഘട്ടത്തിൽ, ഈ ചോദ്യം പരിഹരിക്കാൻ കഴിയുന്ന സോൾവർ കോഡിൻ്റെ പ്രെഡിക്ഷൻ  “convert_text_to_number” ആയിരിക്കുമെന്ന് ഞങ്ങൾ കരുതുന്നു. 

അടുത്ത ഘട്ടത്തിൽ, പ്രവചനം അനുസരിച്ച്   സോൾവറിന് മൂല്യനിർണ്ണയം നടത്താനുള്ള ആർഗ്യുമെൻ്റ് ഞങ്ങൾ കൊണ്ടുവരുന്നു. അതിനാൽ, ഈ സാഹചര്യത്തിൽ സോൾവറിലേക്കുള്ള ഇൻപുട്ട് ആർഗ്യുമെൻ്റ് “രണ്ട് ലക്ഷത്തി അൻപതിനായിരത്തി തൊള്ളായിരത്തി മുപ്പത്തിയാറ്” ആയിരിക്കും.

അതിനാൽ, നമുക്ക് പൂർണ്ണമായ സോൾവർ ലഭിക്കും:

വാചകം_നമ്പറിലേക്ക്_പരിവർത്തനം ചെയ്യുക(രണ്ട് ലക്ഷത്തി അൻപതിനായിരത്തി തൊള്ളായിരത്തി മുപ്പത്തിയാറ്).

തുടർന്ന്, ഉത്തരവും ഘട്ടം ഘട്ടമായുള്ള പരിഹാരവും ലഭിക്കുന്നതിനുള്ള ആർഗ്യുമെൻ്റ് ഉപയോഗിച്ച് ഞങ്ങൾ സോൾവറിനെ വിലയിരുത്തുന്നു, അത് ചുവടെ കാണിച്ചിരിക്കുന്നത് പോലെയാണ് :

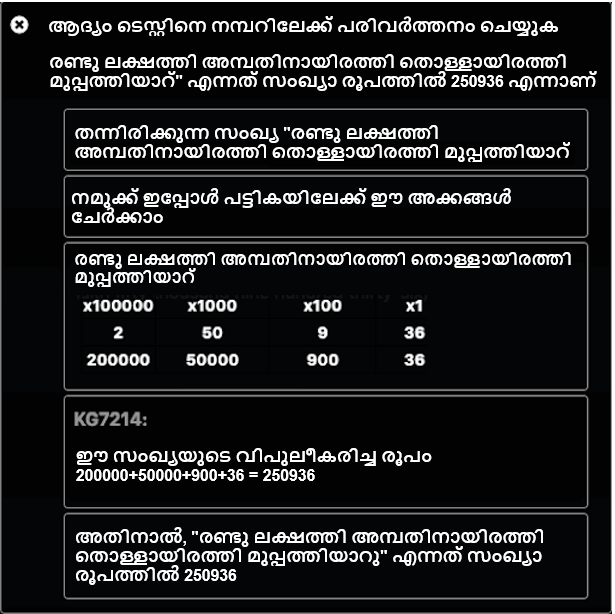
മറ്റൊരു ഉദാഹരണ ചോദ്യം ഉപയോഗിച്ച് നമുക്ക് വിശദീകരിക്കാം:

“ശ്രീമതി  സോണി 7 1/2 ലിറ്റർ പാൽ വാങ്ങി. ഇതിൽ 5 3/4 ലിറ്റർ പാലാണ് ഉപയോഗിച്ചത്. അവളുടെ പക്കൽ എത്ര പാൽ ബാക്കിയുണ്ട്?

“subtract_fractions_mixed_type(7 1/2, 5 3/4)” സോൾവർ കോഡ് ഉപയോഗിച്ച് ഇത് പരിഹരിക്കാവുന്നതാണ്.

പരിഹാര ഘട്ടങ്ങൾ ഇപ്രകാരമാണ്;

പരിഹാരം

നമുക്ക് പരിഹാരം രണ്ട് ഘട്ടങ്ങളായി തിരിക്കാം.

1. സോൾവർ കോഡ്  പ്രെഡിക്ഷൻ 
2. ആർഗ്യുമെൻ്റ് എക്സ്ട്രാക്ഷൻ

സോൾവർ കോഡ്  പ്രെഡിക്ഷനിൽ , നൽകിയിരിക്കുന്ന ഗണിത പ്രശ്നങ്ങൾ പരിഹരിക്കാൻ കഴിയുന്ന സോൾവർ കോഡുകൾ പ്രെഡിക്ട് ചെയ്യാൻ  ഞങ്ങൾ ശ്രമിക്കുന്നു. ഉദാഹരണത്തിന്, മുകളിലെ ഉദാഹരണത്തിൽ, “subtract_fractions_mixed_type” ആണ് ശരിയായ സോൾവർ, അത് ഉപയോഗിച്ച് തന്നിരിക്കുന്ന പ്രശ്നം പരിഹരിക്കാൻ കഴിയും. നമുക്ക് T5[1] പോലുള്ള ഡീപ് ലേണിംഗ് ജനറേറ്റീവ് seq2seq മോഡലുകൾ ഉപയോഗിക്കാം, അത് പ്രശ്‌നം പരിഹരിക്കുന്ന സോൾവർ കോഡ് സൃഷ്ടിക്കും.

ഞങ്ങൾ രണ്ടാം ഘട്ടത്തിലേക്ക് പോകുന്നതിന് മുമ്പ്, ഓരോ സോൾവർ കോഡിനും ആർഗ്യുമെൻ്റുകളുള്ള 1 സാമ്പിൾ സോൾവർ ആവശ്യമാണ്. ഉദാഹരണത്തിന്, “subtract_fractions_mixed_type” എന്നതിനായുള്ള ഒരു സാമ്പിൾ സോൾവർ “subtract_fractions_mixed_type(1 2/3, 4 5/6)” പോലെയായിരിക്കാം. ഇതിനെ എങ്ങനെ ഉപയോഗത്തിൽ കൊണ്ട് വരാം എന്നത്തിലേക്കുള്ള ഗവേഷണം ഞങ്ങൾ ഉടൻ തുടങ്ങും. 

പ്രവചിച്ച സോൾവർ കോഡ് ലഭിച്ചുകഴിഞ്ഞാൽ, നൽകിയിരിക്കുന്ന പ്രശ്നം പരിഹരിക്കാൻ കഴിയും, ചോദ്യത്തിൽ നിന്ന് ആർഗ്യുമെൻ്റുകൾ കണ്ടെത്തേണ്ടതുണ്ട്. അതിനായി, നമുക്ക് T5[1] പോലെയുള്ള ജനറേറ്റീവ് seq2seq മോഡലുകൾ ഉപയോഗിക്കാം. നോളേജ് ഗ്രാഫുകളിൽ അടങ്ങിയിരിക്കുന്ന  അർത്ഥപരമായ ബന്ധങ്ങളെ സ്വാധീനിക്കുന്നതിനായി നോളേജ്  ഇൻഫ്യൂഷൻ ആർക്കിടെക്ചർ ഉപയോഗിച്ച് അത്തരം ഭാഷാ മാതൃകകൾ കൂടുതൽ വിപുലീകരിക്കുന്നു [3][4]. പ്രെഡിക്ടഡ്  സോൾവറിനായി നമുക്ക് പ്രോബ്ലം സ്റ്റേറ്റ്മെൻ്റും സാമ്പിൾ സോൾവറും നൽകാം. കൂടാതെ T5[1] മോഡലിൽ നിന്നുള്ള ചോദ്യങ്ങളിൽ നിന്ന് യഥാർത്ഥ ആർഗ്യുമെൻ്റുകളുള്ള സോൾവർ കോഡ് നമുക്ക് ലഭിക്കും. അതിനാൽ അവസാനം നമുക്ക് ആർഗ്യുമെൻ്റുകളുള്ള സോൾവർ കോഡ് ലഭിക്കും, അതായത് മുകളിലുള്ള ഉദാഹരണത്തിൽ നിന്ന് “subtract_fractions_mixed_type(7 1/2, 5 3/4)”.

ചോദ്യത്തിൽ നിന്ന് ആർഗ്യുമെൻ്റുകൾ കണ്ടെത്തുന്നതിന് താരതമ്യേന ലളിതമായ മറ്റ് രീതികളും നമുക്ക് ഉപയോഗിക്കാം. അതുപോലെ, ഓരോ സോൾവറിനുമുള്ള ആർഗ്യുമെൻ്റുകളുടെ ഡാറ്റ തരങ്ങളും സാമ്പിളുകളും ഞങ്ങളുടെ പക്കലുണ്ടെങ്കിൽ, ചോദ്യത്തിൽ നിന്ന് സമാനമായ സംഖ്യകൾ ലഭ്യമാക്കാൻ നമുക്ക് ശ്രമിക്കാം.

ഇങ്ങനെയാണ് ഞങ്ങൾ സോൾവർ കോഡ് പ്രവചിക്കുകയും ചോദ്യത്തിൽ നിന്ന് സോൾവർ ആർഗ്യുമെൻ്റുകൾ കണ്ടെത്തുകയും ചെയ്യുന്നത്. നമുക്ക് അവ രണ്ടും ലഭിച്ചുകഴിഞ്ഞാൽ, ശരിയായ ഉത്തരവും ഘട്ടം ഘട്ടമായുള്ള പരിഹാരവും ലഭിക്കുന്നതിന് സോൾവർ കോഡ് നോക്കിയാൽ  മതിയാകും.

References

[1] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, Peter J. Liu. “Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer”

[2] Amini, Aida, Saadia Gabriel, Peter Lin, Rik Koncel-Kedziorski, Yejin Choi, and Hannaneh Hajishirzi. “MathQA: Towards interpretable math word problem solving with operation-based formalisms.” arXiv preprint arXiv:1905.13319 (2019).

[3] Faldu, Keyur, Amit Sheth, Prashant Kikani, and Hemang Akabari. “KI-BERT: Infusing Knowledge Context for Better Language and Domain Understanding.” arXiv preprint arXiv:2104.08145 (2021).

[4] Gaur, Manas, Keyur Faldu, and Amit Sheth. “Semantics of the Black-Box: Can knowledge graphs help make deep learning systems more interpretable and explainable?.” IEEE Internet Computing 25, no. 1 (2021): 51-59.