Area Under Simple Curves

The area of the region between the curves  $y=\sqrt{\frac{1+\sin x}{\cos x}}$  and  $y=\sqrt{\frac{\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}1-\sin x}{\cos x}}$  bounded by the lines  $x=0$  and  $x=\frac{\pi }{4}$  is:

Line $L$ passes through the points $\left(-0.25,0\right)$ and $\left(1,10\right)$. Consider the region bounded by the graph of line $L$ for $-0.25\le x\le 1$, the curve $y=(x-4{)}^2+1$ for $1\le x\le 6$ and the $x$ axis. The region is shown below

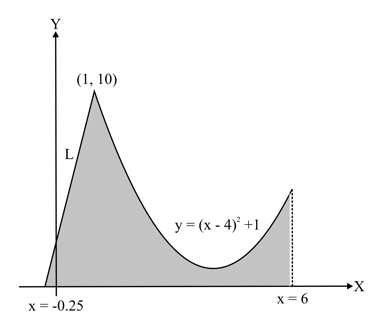
If the area of the shaded region is $k$ sq. units, then the value of $12k$ is

Line $L$ passes through the points $\left(-0.25,0\right)$ and $\left(1,10\right)$. Consider the region bounded by the graph of line $L$ for $-0.25\le x\le 1$, the curve $y=(x-4{)}^2+1$ for $1\le x\le 6$ and the $x$ axis. The region is shown below

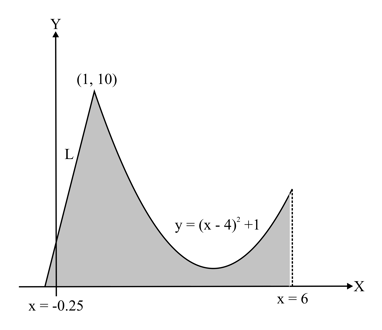
Write down the expression for the area under the curve $y=(x-4{)}^2+1$ for $1\le x\le 6.$

Line $L$ passes through the points $\left(-0.25,0\right)$ and $\left(1,10\right)$. Consider the region bounded by the graph of line $L$ for $-0.25\le x\le 1$, the curve $y=(x-4{)}^2+1$ for $1\le x\le 6$ and the $x$ axis. The region is shown below

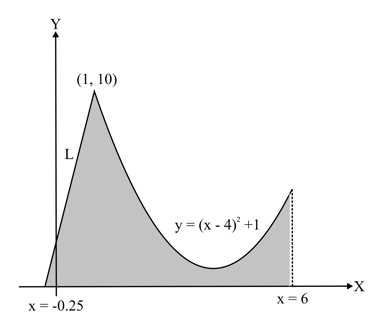
If the area under the graph of $L$ for $-0.25\le x\le 1$ is $k$ sq. units, then the value of $k$ is

Consider the area enclosed by the curve $y=5-\frac{x^3}{25}$ and the positive $x$-axis and $y$-axis. If the shaded area is $k$ sq. units, then the value of $k$ is

Consider the area enclosed by the curve $y=5-\frac{x^3}{25}$ and the positive $x$-axis and $y$-axis.

Using the trapezium rule with five strips, determine an approximation for the shaded area.

Using integration, determine the exact value of the shaded area.

Find the percentage error of your approximation, compared with the exact value.

The diagram below shows an area bounded by the x-axis,the line $$$x=6$,the line $y=2x-2$ and the curve $y=\frac{36}{x^2}$.

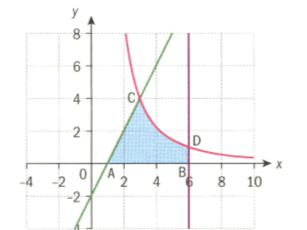
The coordinates of points $A,B,C$ and $D$ are $A(1,0) , B(6,0) , C(3,4) , D(6,1)$

Show that the shaded area is exactly $10$ square units.

The diagram below shows an area bounded by the x-axis,the line $$$x=6$,the line $y=2x-2$ and the curve $y=\frac{36}{x^2}$.

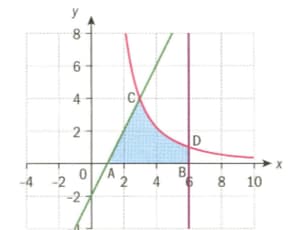
Using technology or otherwise, find the coordinates of points $A,B,C$ and $D$ 

Consider the curve$y=-\frac{x^2}{10}\left(x-10\right)$ 

The area $A$ is defined as the region bounded by the curve and the $x$-axis.

Find the exact value of $A$.

Consider the curve$y=-\frac{x^2}{10}\left(x-10\right)$ 

The area $A$ is defined as the region bounded by the curve and the x-axis.

Write down a definite integral that represents $A$

Find the coordinates of the points of intersection of the graph of $y=6x-x^2$ and $y=10-x$.

The table below shows the coordinates $\left(x,y\right)$ of five points that lie on a curve $y=f\left(x\right)$.

$\begin{array}{|llcccc|}\hline x& 1& 3.25& 5.5& 7.75& 10\\ y=f\left(x\right)& 3& 9& 7& 12& 5\\ \hline\end{array}$

Estimate the area under the curve over the interval $1\le x\le 10.$

Consider the graph of the function $f\left(t\right)=-t^2+2t$ where $f\left(t\right)\ge 0$. Draw the graph of the function $f$ and shade the area enclosed between this graph and the $t$-axis over the interval $0\le t\le x$. Find an expression for the area under the graph of $f$ over the interval $0\le t\le x$.

Consider the graph of the function $f\left(t\right)=4t$ over the interval $3\le t\le x$. Find ${\int }_3^{x}4t \mathrm{d}t$.

Consider the graph of the function $f\left(x\right)={\left(x+2\right)}^2+1.$ The region bounded by the graph of $f$ the $x$-axis, the $y$-axis and the vertical line $x=b$ with $b>0$ has an area equal to $42$. Find the value of $b$.

Consider the graph of the function $f\left(x\right)={\left(x+2\right)}^2+1.$ The region bounded by the graph of $f$ the $x$-axis, the $y$-axis and the vertical line $x=b$ with $b>0$ has an area equal to $42$. Sketch the region.

Consider the curve $y=x^3$. Let $A$ be the region enclosed between this curve, the $x$-axis, and the vertical line $x=2$. Sketch the curve and clearly label $A$

Consider the curve $y=x^3$. Let $A$ be the region enclosed between this curve, the $x$-axis, and the vertical line $x=2$. Write down a definite integral that represents the area of $A$. Find the value of this area.

Consider the curve $y=x^3$. Let $A$ be the region enclosed between this curve, the $x$-axis, and the vertical line $x=2$. Write down a definite integral that represents the area of $A$.

Consider the curve $y=x(x-4{)}^2$. Let $A$ be the region enclosed between this curve and the $x$-axis. Write down a definite integral that represents the area of $A$. Find the value of this area.