A K Upadhyay and S Upadhyay Solutions for Chapter: Introduction to Euclid's Geometry, Exercise 2: EXERCISE 5.1

In a parallelogram $\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$, diagonals $\mathrm{A}\mathrm{C}$ and $\mathrm{B}\mathrm{D}$ bisect at $\mathrm{O}$, show that $\mathrm{O}\mathrm{A}+\mathrm{O}\mathrm{B}=\mathrm{O}\mathrm{C}+\mathrm{O}\mathrm{D}.$

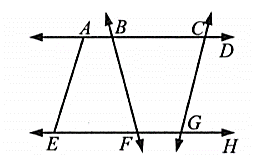
In the figure given below, Name three line segments.

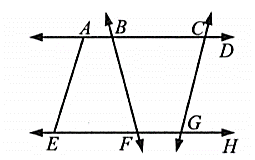
In the figure given below, Name the Four collinear points:

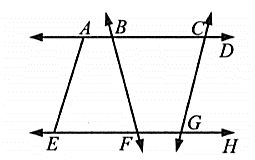
In the figure given below, Name the two pairs of non-intersecting line segments:

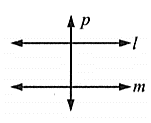
In figure, a line $p$ is perpendicular to both the line $l$ and $m$. Prove that $l\parallel m$ by using Euclid’s fifth postulate.

In the given Figure, $\mathrm{A}\mathrm{B}=\mathrm{C}\mathrm{D}$ and $\mathrm{B}\mathrm{C}=\mathrm{D}\mathrm{E}$. By using Euclid's axiom, prove that $\mathrm{C}$ is the mid point of $\mathrm{A}\mathrm{E}$.

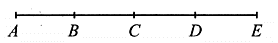
In the given Figure, $\mathrm{A}$ and $\mathrm{B}$ are the centres of the circles. Prove that $∆\mathrm{A}\mathrm{B}\mathrm{C}$ is equilateral.

Solve the equation $x-15=25$ and state Euclid’s axiom used here.