Elastic and Inelastic Collisions

In a collinear collision, a particle with an initial speed $v_0$ strikes a stationary particle of the same mass. If the final total kinetic energy is $50\%$ greater than the original kinetic energy, the magnitude of the relative velocity between the two particles after collision is

A block of mass $0.50 \mathrm{kg}$ is moving with a speed of $2.00 \mathrm{m} {\mathrm{s}}^{-1}$ on a smooth surface. It strikes another mass of $1.00 \mathrm{kg}$ and then they move together as a single body. The energy loss during the collision is:

A point mass of $1 \mathrm{kg}$ collides elastically with a stationary mass of $5 \mathrm{kg}$. After their collision, the $1 \mathrm{kg}$ mass reverses its direction and moves with a speed of $2 \mathrm{m} {\mathrm{s}}^{-1}$. Which of the following statement(s) is (are) correct for the system of these two masses

A particle of mass $m$ is projected from the ground with the initial speed $u_0$ at an angle $\alpha$ with the horizontal. At the highest point of the trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed $u_0$. The angle that the composite system makes with horizontal immediately after the collision is

A particle of mass $m$ moving in the $\mathrm{x}$-direction with speed $2v$ is hit by another particle of mass $2\mathrm{m}$ moving in the $y$-direction with speed $v$. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to,

A particle of mass $m_1$ collides elastically with a stationary particle of mass $m_2\left(m_1>m_2\right)$. Find the maximum angle through which the striking particle may deviate as a result of the collision.

A particle of mass $m$ having collided with a stationary particle of mass $M$ deviated by an angle $\frac{\mathrm{\pi }}{2}$ whereas the particle $M$ recoiled at an angle $\text{θ}=30°$ to the direction of the initial motion of the particle $m$. How much (in per cent) and in what way has the kinetic energy of this system changed after the collision, if $\frac{M}{m}$ $=5.0$?

The particle $1$ moving with velocity $v=10 \mathrm{m} {\mathrm{s}}^{-1}$ experienced a head-on collision with a stationary particle $2$ of the same mass. As a result of the collision, the kinetic energy of the system decreased by $\eta =1.0 \%$. Find the magnitude and direction of the velocity of the particle $1$ after the collision.

A ball moving translationally collides elastically with another, stationary, ball of the same mass. At the moment of impact, the angle between the straight line passing through the centre of the balls and the direction of the initial motion of the striking ball is equal to $\alpha =45°$. Assuming the balls to be smooth, find the fraction $\eta$ of the kinetic energy of the striking ball that turned into potential energy at the moment of the maximum deformation.

Particle $1$ experiences a perfectly elastic collision with a stationary particle $2$. Determine their mass ratio, if

$\left(a\right)$ after a head-on collision the particles fly apart in the opposite directions with equal velocities, 

$\left(b\right)$ the particles fly apart symmetrically relative to the initial motion direction of particle 1 with the angle of divergence $\text{θ}=60°$.

A particle of mass $m_1$ experienced a perfectly elastic collision with a stationary particle of mass $m_2$. What fraction of the kinetic energy does the striking particle lose, if 

$\left(a\right)$ it recoils at right angles to its original motion direction, 

$\left(b\right)$ the collision is a head-on one?

A neutron is scattered through ($\equiv$ deviation from its original direction) $\mathrm{\theta }$ degree in an elastic collision with an initially stationary deuteron. If the neutron loses $\frac{2}{3}$ of its initial $K\mathit{.}E\mathit{.}$ to the deuteron then find the value of $\mathrm{\theta }.$ (In atomic mass unit, the mass of a neutron is $1 \mathrm{u}$ and mass of a deuteron is $2 \mathrm{u}$).

A steel ball falling vertically strikes a fixed rigid plate A with velocity${\mathrm{v}}_{0 }$and rebounds horizontally. The ball then strikes a second fixed rigid plate B and rebounds vertically as shown. Assuming smooth surface and the effect of gravity on motion of ball is to be neglected. Determine

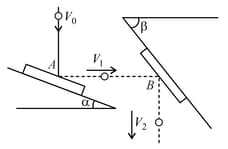
     $\left(\mathrm{a}\right)$ The required angles $\mathrm{\alpha } \mathrm{and} \mathrm{\beta }.$ 

$\left(\mathrm{b}\right)$ The magnitude of the velocity ${\mathrm{v}}_1 \& {\mathrm{v}}_2.$Consider coefficient of restitution for both plates as $\mathrm{e}.$

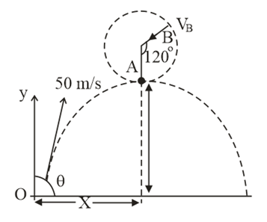
A bullet of mass $M$ is fired with a velocity $50 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle with the horizontal. At the highest point of its trajectory, it collides head on with a bob of mass $3M$ suspended by a massless rod of length $\frac{10}{3} \mathrm{m}$ and gets embedded in the bob. After the collision, the rod moves through an angle $120°.$ Find

$\left(\mathrm{a}\right)$ The angle of projection.
$\left(\mathrm{b}\right)$ The vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$

Two smooth spheres of the same radius, but which have different masses$m_1 \& m_2$collide inelastically. Their velocities before collision are $13 \mathrm{m} {\mathrm{s}}^{-1} \& 5 \mathrm{m} {\mathrm{s}}^{-1}$ respectively along the directions shown in the figure in which $\mathrm{cot\theta } = \frac{5}{12}.$An observer $\mathrm{S}\text{'}$ moving parallel to the positive y - axis with a constant speed of $5 \mathrm{m} {\mathrm{s}}^{-1}$ observes this collision. He finds the final velocity of ${\mathrm{m}}_1$ to be $5 \mathrm{m} {\mathrm{s}}^{-1}$ along the y - direction and the total loss in the kinetic energy of the system to be $\frac{1}{72}$ of its initial value. Determine; 

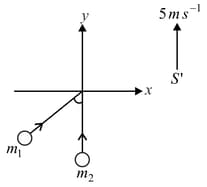
$\left(\mathrm{a}\right)$ The ratio of the masses

$\left(\mathrm{b}\right)$ The velocity of ${\mathrm{m}}_2$ after collision with (respect to observer)

The mass of a hydrogen molecule is $3.32\times {10}^{–27} \mathrm{kg}.$ If ${10}^{23}$ hydrogen molecules strike per second, a fixed wall of area $2 {\mathrm{cm}}^2$ at an angle of $45°$ to the normal and rebound elastically with a speed of ${10}^3 \mathrm{m} {\mathrm{s}}^{-1},$ then the pressure on the wall is nearly: 

It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is $p_{\mathrm{d}},$ while for its similar collision with carbon nucleus at rest, fractional loss of energy is $p_{\mathrm{c}}$. The values of $p_{\mathrm{d}} \mathrm{and} p_{\mathrm{c}}$, respectively.

Statement-1: Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.

Statement-2: Principle of conservation of momentum holds true for all kinds of collisions.

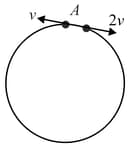
Two small particles of equal masses start moving in opposite directions from a point $A$ in a horizontal circular orbit. Their tangential velocities are $v \text{and} 2v,$respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at $A,$ these two particles will again reach the point $A?$

Statement-1: In an elastic collision between two bodies, the relative speed of the bodies after collision is equal to the relative speed before the collision.

Statement-2: In an elastic collision, the linear momentum of the system is conserved.