Torque

A uniform wooden stick of mass $1.6 \mathrm{kg}$ of length $l$ rests in an inclined manner on a smooth, vertical wall of height $h\left(<l\right)$ such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of $30°$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio $\frac{h}{l}$ and the frictional force $f$ at the bottom of the stick are $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

In case of torque of a couple if the axis is changed by displacing it parallel to itself, torque will :

A force $\overrightarrow{F}=A\hat{\mathrm{i}}+B\hat{\mathrm{j}}$ is applied to a point whose radius vector, relative to the origin of coordinates $O$, is equal to $\overrightarrow{r}=a\hat{\mathrm{i}}+b\hat{\mathrm{j}}$, where $a$, $b$, $A$ and $B$ are constants, and $\hat{\mathrm{i}}$ and $\hat{\mathrm{j}}$ are the unit vectors along $x$ and $y$-axes. Find the moment $N$ and the arm $l$ of the force $F$, relative to the point $O$.

Consider a bicycle in vertical position accelerating forward without slipping on a straight horizontal road. The combined mass of the bicycle and the rider is $M$and the magnitude of the accelerating torque applied on the rear wheel by the pedal and gear system is $\mathrm{\tau }$. The radius and the moment of inertia of each wheel is $R$ and $I$ (with respect to the axis) respectively. The acceleration due to gravity is $g$. 

(a) Draw the free diagram of the system (bicycle and rider ).

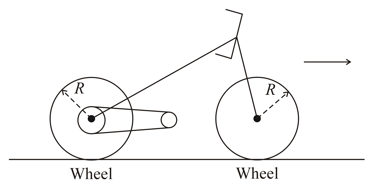
(b) Obtains the acceleration $a$ in terms of the above-mentioned quantities. $a=$

(c) For simplicity assume that the centre of mass of the system is at height $R$ from the ground and equidistant at $2R$ from the centre of each of the wheels. Let $\mathrm{\mu }$ be the coefficient of friction (both static and dynamic) between the wheels and the ground. Consider$M>>\frac{I}{R^2}$ and no slipping. Obtain the conditions for the maximum acceleration $a_{\mathit{m}}$ of the bike. $a_{\mathit{m}}=$

(d) For $\mathrm{\mu } = 1.0$ calculate $a_{\mathit{m}}$ . $a_{\mathit{m}}=$

Two thin circular discs of mass $2 \mathrm{kg}$ and radius $10 \mathrm{cm}$ each are joined by a rigid massless rod of length $20 \mathrm{cm}$. The axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of motion of the truck. The friction with the floor of the truck is large enough, so that object can roll on the truck without slipping. Take $x$-axis as the direction of motion of the truck and $z$-axis as the vertically upward direction. If the truck has an acceleration of $9 \mathrm{m} {\mathrm{s}}^{-2}$, calculate

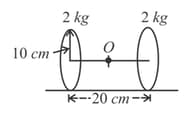
(a) the force of friction on each disc.

(b) the magnitude and direction of frictional torque acting on each disk about the centre of mass $\mathrm{O}$

A bar of mass $m$ is held as shown between $4$ disks, each of mass $M \mathrm{and} \mathrm{radius} r=75 \mathrm{mm}$. Determine the acceleration of the bar immediately after it has been released from rest, knowing that the normal forces exerted on the disks are sufficient to prevent any slipping and assuming that; In (i) case, the discs are attached to the fixed support on wall. In (ii) case, the discs are attached to the bar.

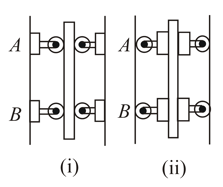
(a) $m=5 \mathrm{kg} \mathrm{and} M=2 \mathrm{kg}$.

(b) the mass of $M$ of the disks is negligible.

(c) the mass of $m$ of the bar is negligible.

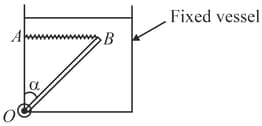
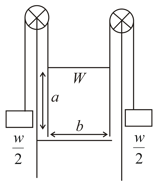
A window (of weight $w$) is supported by two strings passing over two smooth pulleys in the frame of the window in which window just fits in, the other ends of the string being attached to weights each equal to half the weight of the window. One thread breaks and the window moves down. Find acceleration of the window if $\mu$ is the coefficient of friction, and $a$ is the height and $b$ the breadth of the window.

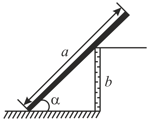
A uniform rod of length $a$ rests against a frictionless wall as shown in figure. Find the friction coefficient between the horizontal surface and the lower end if the minimum angle that the rod can make with the horizontal is $\mathrm{\alpha }$., without slipping.

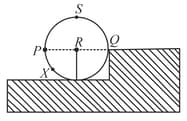
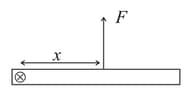
A wheel of radius $R$ and mass $M$ is placed at the bottom of a fixed step of height $R$ as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just climbs the step without slipping. Consider the torque $T$ about an axis normal to the plane of the paper passing through the point $Q$. Which of the following options is/are correct ?

If the positions of two like parallel forces on a light rod are interchanged, their resultant shifts by one-fourth of the distance between them, then the ratio of their magnitude is-

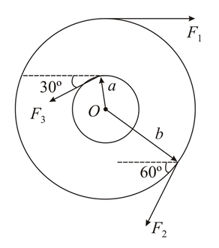
Four forces tangent to the circle of radius $R$ are acting on a wheel as shown in the figure. The resultant equivalent one force system will be

A force $\overrightarrow{F }=4\hat{\mathrm{i}}-10\hat{\mathrm{j}}$ acts on a body at a point having position vector $-5\hat{\mathrm{i}}-3\hat{\mathrm{j}}$ relative to origin of co-ordinates on the axis of rotation. The torque acting on the body about the origin is

A uniform solid sphere is placed on a smooth horizontal surface. An impulse $I$ is given horizontally to the sphere at a height $h=4R/5$ above the centre line. $m$ and $R$ are mass and radius of the sphere, respectively. 

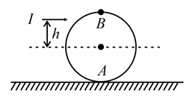
$\left(\mathrm{a}\right)$ Find the angular velocity of the sphere and linear velocity of centre of mass of the sphere after impulse.

$\left(\mathrm{b}\right)$ Find the minimum time after which the highest point $B$ will touch the ground,

$\left(\mathrm{c}\right)$ Find the displacement of the centre of mass during this interval.

A uniform thin rod of length $L$ is hinged about one of its ends and is free to rotate about the hinge without friction. Neglect the effect of gravity.A force$\mathit{ }F\mathit{ }$is applied at a distance $x$ from the hinge on the rod such that force is always perpendicular to the rod. Find the normal reaction at the hinge as function of $x\mathit{,}$ at the initial instant when the angular velocity of rod is zero.

The uniform rod $AB$of mass m is released from rest when $\mathrm{\beta }= 60º.$ Assuming that the friction force between end $A$ and the surface is large enough to prevent sliding, determine (for the instant just after release)

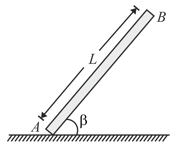
$\left(\mathrm{a}\right)$The angular acceleration of the rod

$\left(\mathrm{b}\right)$ The normal reaction and the friction force at $A.$

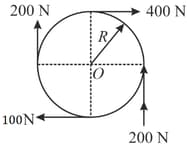
Calculate the net torque on the system about the point $O$ as shown in figure if $F_1=11 \mathrm{N}, F_2=9 \mathrm{N},\mathit{ }{F}_3=10 \mathrm{N}, a=10 \mathrm{cm}$and$b=20 \mathrm{cm}.$(All the forces along the tangent).

A particle having mass $m$ is projected with a speed $v$ at an angle $\alpha$ with horizontal ground. Find the torque of the weight of the particle about the point of projection when the particle (a) is at the highest point. (b) reaches the ground.

A simple pendulum having bob of mass m and length $l$ is pulled aside to make an angle $\mathrm{\theta }$ with the vertical. Find the magnitude of the torque of the weight of the bob about the point of suspension. At which position its torque is zero? At which $\mathrm{\theta }$ it is maximum?

Two forces ${\overrightarrow{F}}_1=2\hat{\mathrm{i}}-5\hat{\mathrm{j}}-6\hat{\mathrm{k}} \text{N}$ and ${\overrightarrow{F}}_2=\hat{\mathrm{i}}+2\hat{\mathrm{j}}-\hat{\mathrm{k}} \text{N}$ are acting on a body at the points $(1, 1, 0)$ and$(0, 1, 2),$ respectively. Find torque acting on the body about point $(–1, 0, 1).$ 

A uniform rod $OB$ of length $1 \mathrm{m}\text{,}$ cross-sectional area $0.012 {\mathrm{m}}^2$ and relative density $2.0$ is free to rotate about $\mathrm{O}$ in vertical plane. The rod is held with a horizontal string $AB$ which can withstand a maximum tension of $45 \mathrm{N}.$ The rod and string system is kept in water as shown in figure. The maximum value of angle $\alpha$ which the rod can make with vertical without breaking the string is