Andhra Pradesh Board Solutions for Chapter: Similar Triangles, Exercise 14: EXERCISE - 8.4
Andhra Pradesh Board Mathematics Solutions for Exercise - Andhra Pradesh Board Solutions for Chapter: Similar Triangles, Exercise 14: EXERCISE - 8.4
Attempt the free practice questions on Chapter 8: Similar Triangles, Exercise 14: EXERCISE - 8.4 with hints and solutions to strengthen your understanding. Mathematics Class 10 solutions are prepared by Experienced Embibe Experts.
Questions from Andhra Pradesh Board Solutions for Chapter: Similar Triangles, Exercise 14: EXERCISE - 8.4 with Hints & Solutions
is a triangle right angle at and is a point on such that . Show that .
is a triangle right angle at and . Show that .
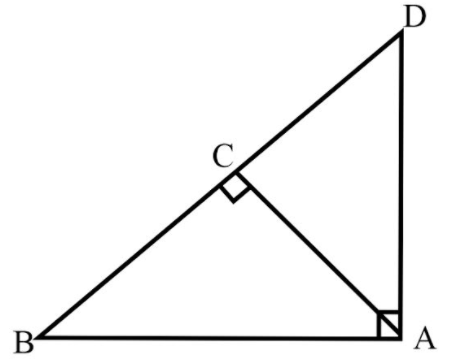
is a triangle right angle at and . Show that .
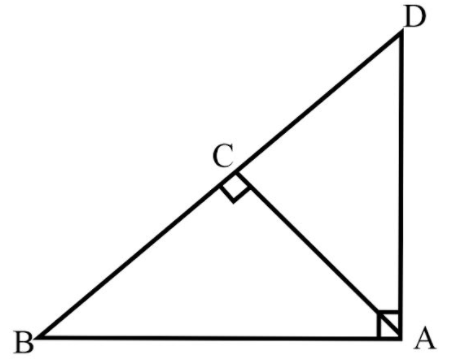
is a triangle right angle at and . Show that .
is an isosceles triangle right angle at . Prove that .
In an equilateral triangle, is a point on side such that . Prove that .
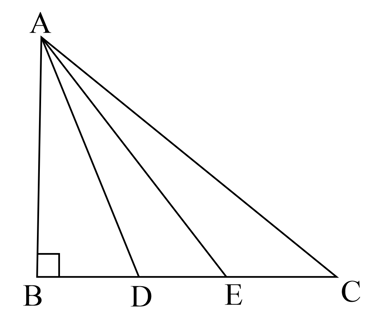
In the given figure, is a triangle right-angled at . and are points on trisect it. Prove that .
is an isosceles triangle right-angled at . Equilateral triangles and are constructed on sides and . Find the ratio between the areas of and .