Andhra Pradesh Board Solutions for Chapter: Similar Triangles, Exercise 15: OPTIONAL EXERCISE
Andhra Pradesh Board Mathematics Solutions for Exercise - Andhra Pradesh Board Solutions for Chapter: Similar Triangles, Exercise 15: OPTIONAL EXERCISE
Attempt the free practice questions on Chapter 8: Similar Triangles, Exercise 15: OPTIONAL EXERCISE with hints and solutions to strengthen your understanding. Mathematics Class 10 solutions are prepared by Experienced Embibe Experts.
Questions from Andhra Pradesh Board Solutions for Chapter: Similar Triangles, Exercise 15: OPTIONAL EXERCISE with Hints & Solutions
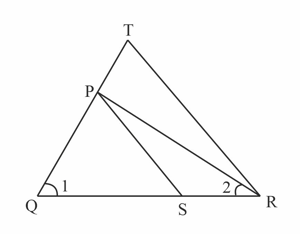
In the figure, and , prove that .
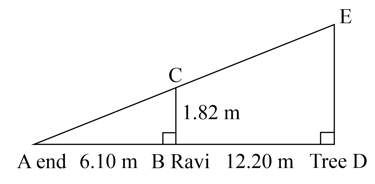
Ravi is tall. He wants to find the height of a tree in his backyard. From the tree's base he walked along the tree's shadow to a position where the end of his shadow exactly overlaps the end of the tree's shadow. He is now from the end of the shadow. How tall is the tree?
The diagonal of a parallelogram intersects at the point , where is any point on side . Prove that .
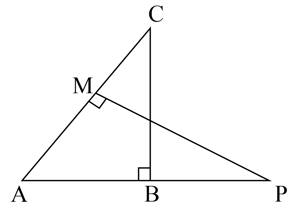
and are two right triangles right-angled at and respectively. Prove that .
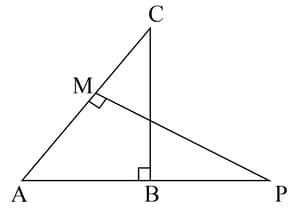
and are two right triangles right-angled at and respectively. Prove that .
An aeroplane leaves an airport and flies due north at a speed of . At the same time another aeroplane leaves the same airport and flies due west at a speed of . How far apart will the two planes be after hours?
In a right triangle right-angled at . and are points on sides and respectively which divide these sides in the ratio of .
Prove that
In a right triangle right-angled at . and are points on sides and respectively which divide these sides in the ratio of .
Prove that .
