Arun Sharma Solutions for Exercise 2: Level of Difficulty

In a $\Delta PQR, X, Y, Z$ are points on sides $PQ, QR, PR$ such that $PX:XQ=1:1, PZ:ZR=1:2, QY:YR=2:3$. What is the ratio of the area of quadrialteral $XYRZ$ to that of $\Delta PXZ$?

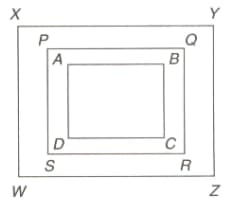
$ABCD$ is a square with sides of length $10$ units. $OCD$ is an isosceles triangle with base $CD$. $OC$ cuts $AB$ at point $Q$ and $OD$ cuts $AB$ at point $P$. The area of trapezoid $PQCD$ is $80$ square units. The altitude from $O$ of the triangle $OPQ$ is:

In a triangle $ABC$ the length of side $BC$ is $295$. If the length of side $AB$ is a perfect square, then the length of side $AC$ is a power of $2,$ and the length of side $AC$ is twice the length of side $AB$. Determine the perimeter of the triangle.

$ABCD$ is a parallelogram with $\angle ABC={60}^{\mathrm{o}}$. If the longer diagonal is of length $7 cm$ and the area of the parallelogram $ABCD$ is $15 \frac{\sqrt{3}}{2} c{m}^2$, then the perimeter of the parallelogram (in $cm$) is:

A city has a park shaped as a right angled triangle. The length of the longest side of this park is $80 m$. The Mayor of the city wants to construct three paths from the corner point opposite to the longest side such that these three paths divide the longest side into four equal segments. Determine the sum of the squares of the lengths of the three paths (in $m^2$)

Let $P_1$ be the circle of radius $r$. $A$ square $Q_1$ is inscribed in $P_1$ such that all the vertices of the square $Q_1$ lie on the circumference of $P_1$. Another square $Q_2$ is inscribed in the circle $P_2$. Circle $P_3$ is inscribed in the square $Q_2$ and so on. If $S_N$ is the area between $Q_N$ and $P_{N-1}$ where $N$ represents the set of natural numbers. If the ratio of sum of all such $S_N$ to that of the area of the square $Q_1$ is $\frac{a-\mathrm{\pi }}{b}$ then $a+b=$?

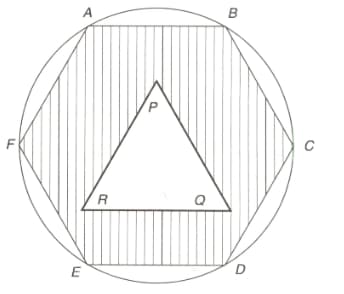
In the figure, $ABCDEF$ is a regular hexagon and $PQR$ is an equilateral triangle of side '$a$'. The area of the shaded portion is $23\sqrt{3} c{m}^2$ and $CD:PQ::2:1$.

If the area of the circle circumscribing the hexagon is $X\pi c{m}^2$ then $X=?$

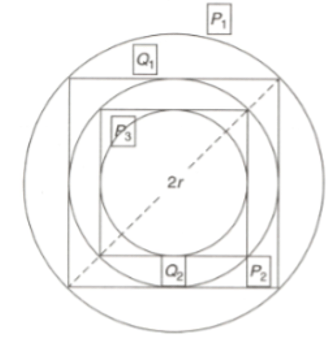
A series of infinite concentric squares are drawn as shown below. Starting with the first square $ABCD,$ subsequent squares drawn are $PQRS, XYZW$ and so on as shown in the diagram. If areas of the squares $ABCD, PQRS, XYZW,...$ are $1, \frac{3}{2}, \frac{7}{4}, \frac{15}{8}...$ and so on, then find the area of the diagram when the infinite number square is drawn.