B M Sharma Solutions for Chapter: Electric Potential, Exercise 5: DPP

Both the ring and the conducting sphere are given the same charge $Q$. Determine the potential of the sphere. Assume that the centre of the sphere lies on the axis of the ring. Is it necessary that the charge on the ring be uniformly distributed to answer the above question?

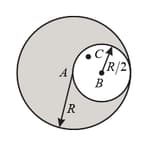
A solid sphere of the radius $R$ has a cavity of radius $\frac{R}{2}.$ The solid part has a uniform charge density $\rho$ and cavity has no charge. Find the electric potential at the point $A$. Also, find the electric field (only magnitude) at a point $C$ inside the cavity.

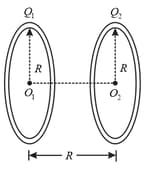
A thin spherical conducting shell of the radius $R$ has a charge $q$. Another charge $Q$ is placed at the centre of the shell. The electrostatic potential at a point $P$ at a distance $\frac{R}{2}$ from the centre of the shell is

An arc of radius $r$ carries a charge. The linear density of charge is $\lambda$ and the arc subtends an angle $\frac{\pi }{3}$ at the centre. What is the electric potential at the centre?

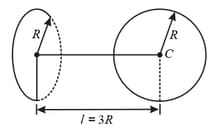
Two identical thin rings each of radius $R$ meters are coaxially placed at a distance $R$ meters apart. If $Q_1$ coulomb and $Q_2$ coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge $q$ from the centre of one ring to that of other is

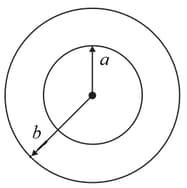
If the electric potential of the inner shell is $10$ volt and that of the outer shell is $5$ volt, then the potential at the centre will be: (the shells are uniformly charged) 

The potential difference between the centre and the surface of the sphere of radius $R$ and having uniform volume charge density $\rho$ within it will be

A mercury drop has potential $V$ on its surface. $1000$ such drops combine to form a new drop. Find the potential on the surface of the new drop.