B M Sharma Solutions for Chapter: Kinetic Theory of Gases, Exercise 3: Exercises

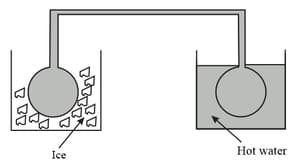
Two identical glass bulbs are interconnected by a thin glass tube at $0 \text{°C}$. A gas is filled in these bulbs. If one bulb is placed in ice and another bulb is placed in hot bath, the pressure of the gas become $1.5$ times. The temperature of hot bath will be.

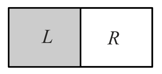
A vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases are filled in left $\left(L\right)$ and right $\left(R\right)$ halves. The root-mean-square speed of the molecules in $L$ part is equal to the mean speed of molecules in the $R$ part. Then the ratio of the mass of a molecule in $L$ part to that of a molecule in $R$  part is:-

If $22 \mathrm{g}$ of ${\mathrm{CO}}_2$ at $27°\mathrm{C}$ is mixed with $16 \mathrm{g}$ of ${\mathrm{O}}_2$ at $37°\mathrm{C}$, the temperature of the mixture is 

A closed vessel contains a mixture of two diatomic gases $A$ and $B$. Molar mass of $A$ is $16$ times that of $B$ and mass of gas $A$ contained in the vessel is $2$ times that of $B$. Choose the correct statement($\mathrm{s}$).

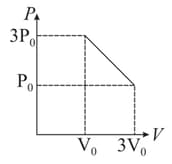
$n$ moles of a gas in a cylinder under a piston are transferred to infinitely slowly from a state with a volume of $V_0$ and a pressure $3P_0$ atoms to state with $3V_0$ and a pressure $P_0$ as shown in figure. If the maximum temperature that the gas will reach in this process is $\frac{x{P}_0{V}_0}{ nR}$, what is the value of $x?$

An ideal gas has a volume $0.3{ \mathrm{m}}^3$ at $150 \mathrm{kPa}$. It is confined by a spring-loaded piston in a vertical cylinder. Initially, the spring is in relaxed state. If the gas is heated to a final state of $0.5{ \mathrm{m}}^3$ and pressure $600 \mathrm{kPa}$, find the work done (in $\mathrm{kJ}$) on the spring (atmospheric pressure, $P_0=1\times {10}^5 \mathrm{N} {\mathrm{m}}^{-2}$).

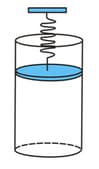
Oxygen is filled in a closed metal jar of volume $1.0\times {10}^{-3}{ \mathrm{m}}^3$at a pressure of $1.5\times {10}^5 \mathrm{Pa}$ and temperature $400 \mathrm{K}$. The jar has a small leak in it. The atmospheric  pressure is $1.0\times {10}^5 \mathrm{Pa}$ and the atmospheric temperature is $300 \mathrm{K}$. Find the mass (in $\mathrm{g}$) of the gas that leaks out by the time the pressure and the temperature inside the jar equalise with the surrounding.

Figure shows a vertical cylindrical vessel separated in two parts by a frictionless piston free to move along the length of the vessel. The length of the cylinder is $1.0 \mathrm{m}$ and the piston divides the cylinder in the ratio of $3:2$. Each of the two parts of the vessel contains $0.2$ mole of an ideal gas. The temperature of the gas is $300 \mathrm{K}$ in each part. Calculate the mass of the piston. (in $\mathrm{kg}$)