B M Sharma Solutions for Chapter: Travelling Waves, Exercise 2: CONCEPT APPLICATION EXERCISE

A wave is propagating on a long stretched string along its length taken as the positive $x$ -axis. The wave equation is given as $y=y_0{e}^{-{\left(\frac{t}{T}-\frac{x}{\lambda }\right)}^2}$ where $y_0=4 \mathrm{mm}$, $T=1.0 \mathrm{s}$ and $\lambda =4 \mathrm{cm}$.

Find the function $g\left(x\right)$ giving the shape of the string at $t=0$

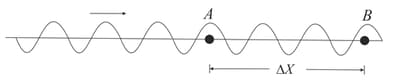
There are two corks A and B at a separation $\Delta x$, lying on a water wave. Assume it as a transverse wave having wavelength $\lambda$ moving along $+x$ -direction. Find $\mathrm{\Delta x}$ if the

momenta of two identical corks on the wave will be equal.

Two tuning forks separated by a distance $l$ each of frequency $f=150 \mathrm{Hz}$ with zero initial phase. If the wave speed is $10 \mathrm{m}/\mathrm{s}$, at a distance $x=\frac{l}{4}$, find the phase difference between these two waves.

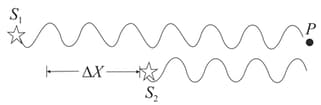
Two sources $S_1$ and $S_2$ emit transverse wave with wavelengths $\lambda =1 \mathrm{m}$ and having zero phase angles. If their frequency is $10 \mathrm{Hz}$ and the separation distance between the sources is $\Delta x=\frac{1}{4} \mathrm{m}$. Find the phase difference between the waves at some point ( say P) if the sources start emitting waves at

$t=0$ simultaneously

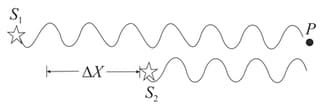
Two sources $S_1$ and $S_2$ emit transverse wave with wavelengths $\lambda =1 \mathrm{m}$ and having zero phase angles. If their frequency is $10 \mathrm{Hz}$ and the separation distance between the sources is $\Delta x=\frac{1}{4} \mathrm{m}$. Find the phase difference between the waves at some point ( say P) if the sources start emitting waves at

$t_1=0$ and ${\mathrm{t}}_2=1\mathrm{s}$ respectively.

The equation of a progressive wave is given by $y=0.20\sin 2\pi \left(60t-\frac{x}{5}\right)$ where $x$ and $y$ are in metre and tis in second. Find the

phase difference between two particles separated by a distance of $\Delta x=125 \mathrm{cm}$,

The equation of a progressive wave is given by $y=0.20\sin 2\pi \left(60t-\frac{x}{5}\right)$ where $x$ and $y$ are in metre and tis in second. Find the

phase difference between the instants $1/120 \mathrm{s}$ and $1/40 \mathrm{s}$, for any particle.

The equation of a progressive wave is given by $y=0.20\sin 2\pi \left(60t-\frac{x}{5}\right)$ where $x$ and $y$ are in metre and tis in second. Find the

position/s of the particle/s which differ by a phase difference of $\Delta \theta =\pi /3$, with respect to that at position $x=10 \mathrm{m}$