B M Sharma Solutions for Chapter: Electric Flux and Gauss's Law, Exercise 3: Exercise

The figure shows, in cross-section, two Gaussian spheres and two Gaussian cubes that are centered on a positively charged particle. Rank greatest first, and indicate whether the magnitudes are uniform or variable along each surface.

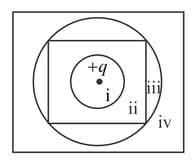
The figure shows four Gaussian surfaces consisting of identical cylindrical midsections but different end caps. The surfaces are in a uniform electric field that is directed parallel to the central axis of each cylindrical midsection. The end caps have these shapes: $S_1$, convex hemispheres; $S_2$, concave hemispheres; $S_3$, cones; $S_4$, flat disks. Rank the surfaces according to $\left(\mathrm{a}\right)$ the net electric flux through them and $\left(\mathrm{b}\right)$ the electric flux through the top end caps, the greatest first.

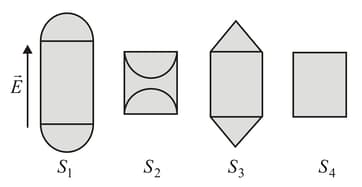
The figure shows a neutral metallic sphere with a point charge $+Q$ placed near its surface. Electrostatic equilibrium conditions exist on the metallic sphere. Mark the correct statements.

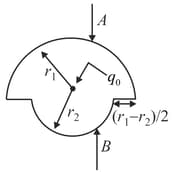
$A$ and $B$ are semi-spherical surfaces of radius $r_1$ and $r_2$ $\left(r_1>r_2\right)$ with $E_1$ and $E_2$ as the electric fields at their surfaces. Charge $q_0$ is placed as shown. What is the condition which may be satisfied?

A non-uniform electric field $E=\left(5x\hat{\mathrm{i}}+3\hat{\mathrm{j}}\right) \mathrm{N} {\mathrm{C}}^{-1}$ goes through a cube of side length $2.0 \mathrm{m}.$ oriented as shown. Then,

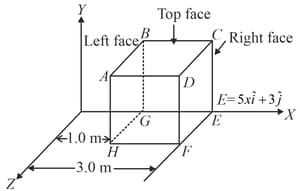
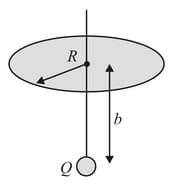
A point charge $Q$ is located on the axis of disc of radius $R$ at a distance $b$ from the plane of the disk. If one fourth of the electric flux from the charge passes through the disk, then $R=\sqrt{\square }b$ (as shown in figure). Suitable value for $\square$ can be,

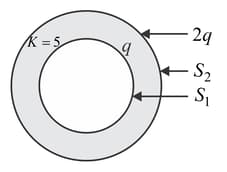
${\mathrm{S}}_1$ and ${\mathrm{S}}_2$ are two hollow concentric spheres with charge $q$ and $2q.$ Space between ${\mathrm{S}}_1$ and ${\mathrm{S}}_2$ is filled with a dielectric of dielectric constant, $K=5$. The ratio of flux through $S_2$ and flux through $S_1$ is $K\text{'}.$ Then find the value of $15K\text{'}.$

Consider a uniform charge distribution with charge density $2 \mathrm{C} {\mathrm{m}}^{-3}$ throughout in space. If a Gaussian sphere has a variable radius which changes at the rate of $2 \mathrm{m} {\mathrm{s}}^{-1}$, then the value of the rate of change of flux is proportional to $r^k$ ($r=$radius of the sphere). Then, find the value of $k$.