B M Sharma Solutions for Chapter: Rigid Body Dynamics: Part 1, Exercise 3: CONCEPT APPLICATION EXERCISE

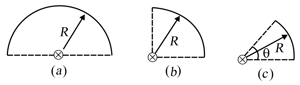
Find out the moment of inertia of the circular ares shown each having mass $M$, radius $R$ and having uniform mass distribution about an axis passing through the centre and perpendicular to the plane.

Calculate the moments of inertia of the figures shown, each having uniform mass distribution about an axis perpendicular to the plane and passing through the centre.

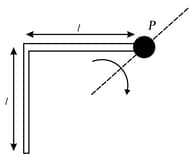
Find the moment of inertia of the two uniform joint rods about point $P$ as shown in figure. Use parallel axis theorem. Mass of each rod is $M$..

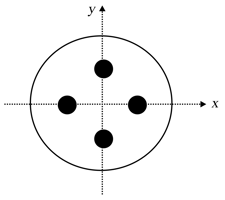
A uniform disc of mass $m$ and radius $R$ has an additional rim of mass $m$ as well as four symmetrically placed masses, each of mass $m/4$, tied at positions $R/2$ from the centre as shown in figure. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?

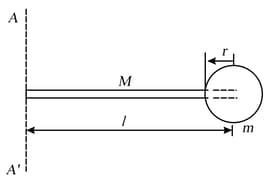
Find the moment of inertia of a spherical ball of mass $m$ and radius $r$ attached at the end of a straight rod of mass $M$ and length $l$, if this system is Ifee to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

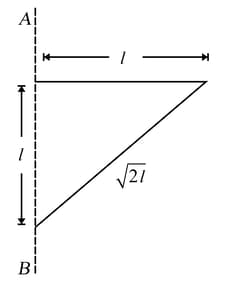
Find moment of inertia of a triangular lamina of mass $M$ about the axis of rotation $AB$ shown in figure.

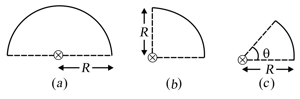
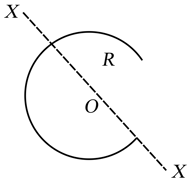
A uniform circular disc of radius $R$ has a sector of angle ${90}^{\mathrm{o}}$ removed from it. Mass of the remaining disc is $M$. Write the moment of inertia of the remaining disc about the axis $xx$ shown in figure.

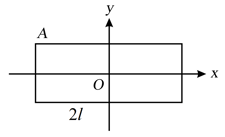
A uniform rectangular plate has side length $l$ and $2l$. The plate lies in $x$- $y$ plane with its centre at origin and sides parallel to $x$- and $y$-axes. The moment of inertia of the plate about an axis passing through a vertex (say $A$) perpendicular to the plane of the figure is $I_0$. Now the axis is shifted parallel to itself so that moment of inertia about it remains $I_0$. Write the locus of point of intersection of the axis with $x$- $y$ plane.